Векторное пространство и его базис
Рассмотрим систему линейных уравнений, определяемую матрицей коэффициентов и расширенной матрицей:
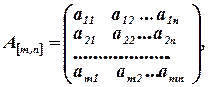
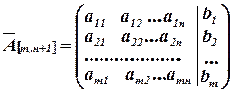 .
.
Известно, что если 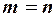 , т.е. число неизвестных равно числу уравнений, и определитель квадратной матрицы коэффициентов
, т.е. число неизвестных равно числу уравнений, и определитель квадратной матрицы коэффициентов
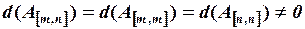 ,
,
то система линейных уравнений является определенной, т.е. имеет одно единственное решение.
Если же 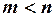 , т.е. число уравнений меньше числа неизвестных, то система линейных уравнений может быть несовместной, т.е. не иметь ни одного решения, либо может быть неопределенной, т.е. иметь множество решений. Другими словами, такая система линейных уравнений не может быть определенной, т.е. не может иметь одно единственное решение.
, т.е. число уравнений меньше числа неизвестных, то система линейных уравнений может быть несовместной, т.е. не иметь ни одного решения, либо может быть неопределенной, т.е. иметь множество решений. Другими словами, такая система линейных уравнений не может быть определенной, т.е. не может иметь одно единственное решение.
Исследуем механизм неопределенности системы линейных уравнений, а именно, как образуется множество решений и какие в нем есть закономерности.
Множество векторов-решений неопределенной системы линейных уравнений образует векторное пространство, в котором определены операции сложения векторов и умножения вектора на число. Если рассматривается неопределенная система линейных уравнений с 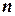 неизвестными, то ее решения составляют
неизвестными, то ее решения составляют 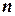 -мерное векторное пространство.
-мерное векторное пространство.
Суммой векторов 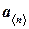 и
и 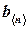 называется вектор:
называется вектор:
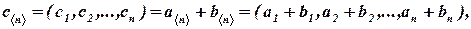
компоненты которого суть суммы соответствующих компонент слагаемых векторов,
где 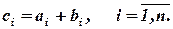
Произведением вектора 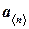 на число
на число 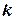 называется вектор:
называется вектор:
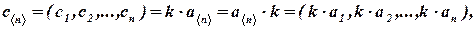
где 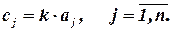
Линейной комбинацией векторов 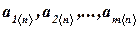 называется вектор
называется вектор 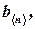 если существуют такие числа
если существуют такие числа 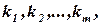 что
что
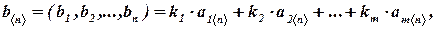
где 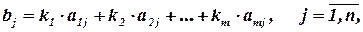
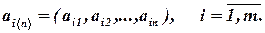
Линейно зависимой называется система векторов 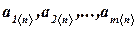 при
при 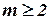 , если хотя бы один из этих векторов является линейной комбинацией других векторов этой системы, и линейно независимой – в противном случае.
, если хотя бы один из этих векторов является линейной комбинацией других векторов этой системы, и линейно независимой – в противном случае.
Тогда, указанная система векторов линейно зависима, если существуют такие числа 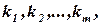 не все равные нулю, для которых выполняется равенство
не все равные нулю, для которых выполняется равенство 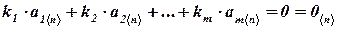 .
.
Если каждый вектор векторного пространства можно представить в виде линейной комбинации векторов из некоторой линейно независимой системы векторов, то такая линейно независимая порождающая система векторов называется базисом векторного пространства.
Примером базиса 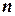 -мерного векторного пространства служит система векторов
-мерного векторного пространства служит система векторов
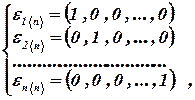
называемых единичными векторами этого пространства.
В 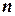 -мерном векторном пространстве существует бесконечно много различных линейно независимых систем векторов. Всякая максимальная линейно независимая система векторов (базис)
-мерном векторном пространстве существует бесконечно много различных линейно независимых систем векторов. Всякая максимальная линейно независимая система векторов (базис) 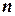 -мерного векторного пространства состоит из
-мерного векторного пространства состоит из 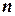 векторов.
векторов.
По аналогии с базисом векторного пространства, порождающим это пространство, решение системы линейных уравнений определяется линейно независимыми строками (столбцами) матрицы коэффициентов (расширенной матрицы) этой системы линейных уравнений. Следовательно, необходимо научиться находить максимальное число линейно независимых строк (столбцов) матрицы.
