Экспериментальные методы ранжирования переменных
Цель работы: Ознакомление с методами ранговой корреляции
Задание:
1. Проверить гипотезу о наличии связи между несколькими рядами рангов, присвоенных объектам в связи с изучаемым явлением (процессом, качеством и т. д.). применить различные методы ранговой корреляции (по Кендалу и по Спирмену).
2. Применить метод конкордации для выяснения степени согласия исследователей в связи с ранжировкой объектов по изучаемому признаку.
Основные теоретические положения.
При изучении сложных процессов, не поддающихся количественному описанию, приходится использовать практический опыт специалистов, работающих в этих областях. При большом числе влияющих факторов мнения специалистов относительно степени влияния этих факторов на процесс могут расходиться. Поэтому возникает задача объективной обработки субъективной информации, которая может быть решена методами ранговой корреляции.
Методы ранговой корреляции.
Ранжирование.
Если n объектов какой-либо совокупности N пронумерованы в соответствии с возрастанием или убыванием какого-либо признака Х, количественно неизмеримого, то говорят, что объекты ранжированы по признаку Х.
Ранг хi указывает то место, которое занимает i-й объект среди других n объектов, расположенных в соответствии с признаком Х (i=1,2,..n).
Ранжирование является менее точным выражением упорядоченной связи объектов относительно какого-либо измеримого или подсчитываемого качества и в этом случае представляет собой замену переменной порядковым номером в прикидочных размерах в целях экономии времени и уменьшения трудоемкости вычислений.
Коэффициент ранговой корреляции.
Коэффициент ранговой корреляции оценивает связь между качественными признаками объектов, не поддающимися точной количественной оценке.
Пусть n объектов ранжированы дважды в соответствии со свойствами X и Y:
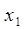
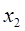 ..
.. 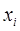 ..
.. 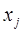 ..
.. 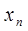
(1)
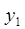
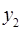 ..
.. 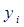 ..
.. 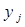 ..
.. 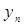
Для объекта i свойства X и Y имеют ранги 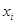 ,
, 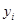 ; для объекта j -
; для объекта j - 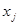 ,
, 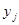 . Пусть связь между рангами
. Пусть связь между рангами 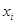 и
и 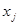 определяется как
определяется как 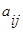 , а между рангами
, а между рангами 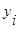 и
и 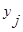 - как
- как 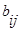 . Наложим такие условия:
. Наложим такие условия:
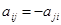
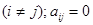
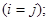
(2)
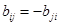
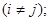
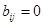
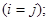
Тогда коэффициент ранговой корреляции определяется как
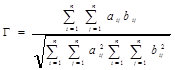 (3)
(3)
Свойства коэффициента ранговой корреляции следующие:
1. 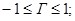
2. Г=0 означает, что признаки X и Y для n объектов не связаны (не коррелированы);
1. Г=1означает, что ранжирование объектов по признаку Х полностью совпадает с ранжированием по признаку Y;
2. Г=-1означает, что ранжирования объектов по признакам X и Y противоположны.
В зависимости от способа определения связи между рангами, выраженного коэффициентами 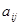 и
и 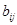 , можно получить различные модификации коэффициента ранговой корреляции Г.
, можно получить различные модификации коэффициента ранговой корреляции Г.
Коэффициент ранговой корреляции по Кендаллу.
Определим величину 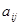 следующим образом:
следующим образом:
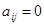 при
при 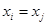 ;
;
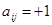 при
при 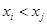 ; (4)
; (4)
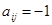 при
при 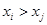 ;
;
Аналогично запишем значения 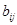 :
:
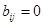 при
при 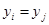 ;
;
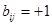 при
при 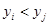 ; (5)
; (5)
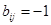 при
при 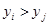 ;
;
Тогда
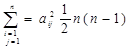 при i<j;
при i<j;
(6)
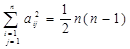 при i<j;
при i<j;
и коэффициент ранговой корреляции по Кендаллу примет вид:
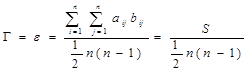 , i<j (7)
, i<j (7)
где величина S равна
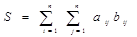 , i<j (8)
, i<j (8)
Пример. Определить, существует ли связь между двумя факторами – производительностью оборудования и степенью его износа. Для этого произведем ранжировку оборудования, обозначенного как №1, №2, №3, №4, №5, №6, по производительности (ряд Х) и по степени износа (ряд Y). Результаты ранжирования приведены в таблице 1.
ТАБЛИЦА 1
| Оборудование | №1 | №2 | №3 | №4 | №5 | №6 |
| Х | ||||||
| Y |
Приведем места по производительности оборудования (Х) к натуральному ряду чисел (табл. 2).
ТАБЛИЦ.А 2
| Оборудование | №4 | №1 | №3 | №2 | №5 | №6 |
| Х | ||||||
| Y |
Все коэффициенты 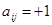 , т. к. ряд Хприведен к натуральному ряду чисел. Коэффициенты
, т. к. ряд Хприведен к натуральному ряду чисел. Коэффициенты 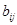 даны в таблице 3.
даны в таблице 3.
ТАБЛИЦА 3.
| I<j | ||||||||||||||
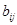 | -1 | -1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 |
Рассчитав величину 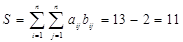 , найдем коэффициент
, найдем коэффициент 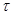 для n=6:
для n=6:
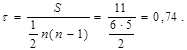
Для ответа на вопрос о связи этих факторов необходимо оценить значимость полученной величины 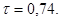
Оценка значимости коэффициента ранговой корреляции по Кендаллу.
Величины S и 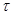 являются случайными. Кривая распределения плотности вероятности величины S симметрична относительно оси, проходящей через S=0, что соответствует отсутствию связи факторов
являются случайными. Кривая распределения плотности вероятности величины S симметрична относительно оси, проходящей через S=0, что соответствует отсутствию связи факторов
Для оценки значимости полученной величины S=1 при n=6 необходимо сравнить её с предельной величиной Sтабл , определяемой по таблице 1 Приложения при уровне значимости 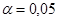 , когда n=6. Если S>Sтабл , то гипотезе об отсутствии связи отвергается. При S<Sтаблгипотеза об отсутствии связи факторов принимается.
, когда n=6. Если S>Sтабл , то гипотезе об отсутствии связи отвергается. При S<Sтаблгипотеза об отсутствии связи факторов принимается.
В рассматриваемом примере Sтабл 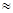 10 при
10 при 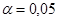 и n=6.
и n=6.
Так как S=11>Sтабл=10, то гипотеза об отсутствии связи факторов не принимается. Это означает, что степень износа оборудования (фактор Y) и производительность оборудования (фактор Х) взаимосвязаны.
Коэффициент ранговой корреляции по Спирмену.
Если определить коэффициенты так:
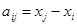 ,
,
при i¹j (11)
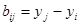 ,
,
то коэффициент ранговой корреляции по Спирмену примет вид
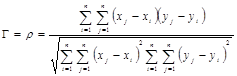 (12)
(12)
Очевидно, что если ряды Х и Y совпадают и представляют натуральные ряды чисел, т. е.
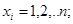
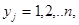 то
то
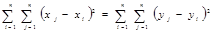 (13)
(13)
Тогда коэффициент 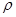 равен
равен
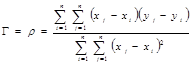 (14)
(14)
Приведем эту формулу к более удобному виду. Так как 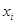 и
и 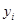 числа натурального ряда, то
числа натурального ряда, то
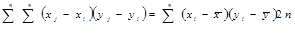 , (15)
, (15)
где 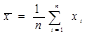 ;
; 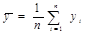 ;
;
Учитывая формулу (15), преобразуем числитель формулы (14) 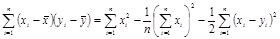 , (16)
, (16)
где 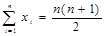 - сумма n членов натурального ряда (17)
- сумма n членов натурального ряда (17)
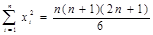 (18)
(18)
тогда числитель формулы (14) принимает вид формулы (19):

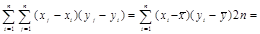
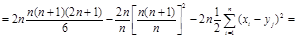
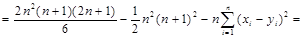
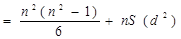 (19)
(19)
 где
где 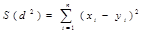 (20)
(20)
Знаменатель формулы (14):
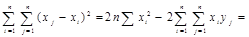
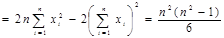 (21)
(21)
Итак, коэффициент ранговой корреляции по Спирмену равен:
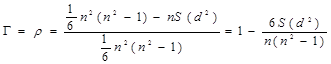 (22)
(22)
При оценке значимости коэффициента ранговой корреляции rнаходим вероятность случайного появления данной или меньшей величины 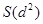 , полученную при объёме выборки n, по таблице 2 Приложения. Полученную вероятность сравниваем с принятым уровнем значимости a, равным 0,05. Если вероятность окажется больше a=0,05, то гипотеза об отсутствии связи между рядами рангов принимается.
, полученную при объёме выборки n, по таблице 2 Приложения. Полученную вероятность сравниваем с принятым уровнем значимости a, равным 0,05. Если вероятность окажется больше a=0,05, то гипотеза об отсутствии связи между рядами рангов принимается.
В примере раздела 3 получен коэффициент ранговой корреляции r, равный 0,77 (таблица 4)
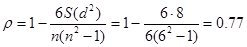
ТАБЛИЦА 4
| Производительность оборудования (x) | ||||||
| Степень износа (y) | ||||||
 | -2 | -1 | ||||
 |
Оценим значимость коэффициента r=0,77, полученную в примере, при 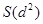 =8 и n=6.
=8 и n=6.
Из таблицы 2 Приложения находим, что вероятность 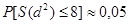 . Так как эта величина находится практически на границе значимости, то примем гипотезу о наличии связи между рядом рангов (таблица 4).
. Так как эта величина находится практически на границе значимости, то примем гипотезу о наличии связи между рядом рангов (таблица 4).
Конкордация(ср.-лат. concordare – быть согласным)
Наиболее интересным практическим приложением ранговой корреляции является вопрос о корреляционной связи нескольких ранжированных рядов.
Пусть имеется ряд объектов 1,2,…,n в различной степени обладающих одним и тем же качеством X, m исследователей ранжируют эти объекты в соответствии с этим качеством. Получается таблица 5 рангов
ТАБЛИЦА 5
| объект (i) исслед. (j) | … | i | … | n | ||
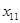 | 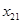 | 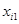 | 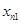 | |||
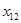 | 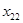 | 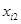 | 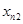 | |||
| … | … | … | … | … | ||
| j | 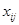 | 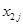 | 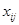 | 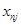 | ||
| … | … | … | … | … | ||
| m | 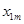 | 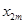 | 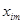 | 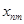 | ||
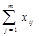 | 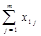 | 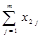 | 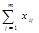 | 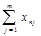 | ||
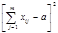 | 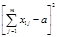 | 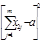 | 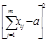 | 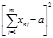 | ||
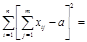 |
Можно было найти коэффициент корреляции (t или r) для каждой пары рядов рангов. При этом пришлось бы вычислять 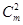 коэффициентов. Притом результат получился бы ненаглядным.
коэффициентов. Притом результат получился бы ненаглядным.
Лучшим способом является определение общего коэффициента ранговой корреляции для всей группы из m исследователей.
В этом случае рассматривают ряд, состоящий из суммарных рангов исследователей для каждого объекта:
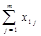
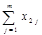 …
… 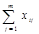 …
… 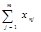 (23)
(23)
Этот ряд рассматривают относительно ряда из n членов, каждый из которых равен среднему значению суммарных рангов ряда (23). Среднее значение суммарных рангов a равно: 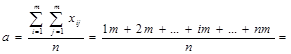
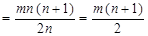 (24)
(24)
В формуле (2) учитывается, что каждый ранг (i=1,2,…,n) повторяется у m исследователей.
Затем находят сумму квадратов отклонений рангов ряда (1) относительно среднего значения рангов:
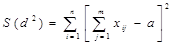 (25)
(25)
Максимальное значение 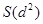 примет тогда, когда исследователи дадут одинаковые ранги, ряды рангов имеют вид натуральных рядов чисел. Тогда ряд из суммарных рангов примет вид:
примет тогда, когда исследователи дадут одинаковые ранги, ряды рангов имеют вид натуральных рядов чисел. Тогда ряд из суммарных рангов примет вид:
m 2m … im … nm (26)
Вычтем из ряда (4) среднее значение a и получим ряд (5)
 …
… 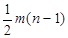 (27)
(27)
Сумма квадратов членов ряда (27) равна
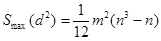 (28)
(28)
Величина W
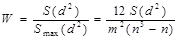 (29)
(29)
называется коэффициентом конкордации. Он оценивает степень согласия мнений исследователей о ранжировании объектов по данному признаку и изменяется в пределах от 0 до 1:
W=0 означает, что связи между ранжировками исследователей не существует;
W=1 означает, что все исследователи одинаково ранжируют объекты.
Величина m(n-1)W имеет 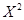 -распределение с n=n-1 степенями свободы:
-распределение с n=n-1 степенями свободы:
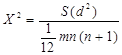 (30)
(30)
Для оценки значимости коэффициента W, полученного с помощью величины 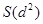 для m исследователей, находят предельное значение
для m исследователей, находят предельное значение 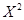 табл., соответствующее a=0,05 при n=n-1.
табл., соответствующее a=0,05 при n=n-1.
При 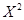 >
> 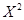 табл. гипотезу об отсутствии связи между ранжировками отвергаем.
табл. гипотезу об отсутствии связи между ранжировками отвергаем.
При 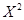 <
< 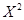 табл. гипотезу об отсутствии связи принимаем.
табл. гипотезу об отсутствии связи принимаем.
Найдём коэффициент конкордации для трёх ранжированных рядов (табл. 6)
ТАБЛИЦА 6
| объект (i) исслед. (j) | n=5 | ||||
| m=3 | |||||
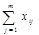 | |||||
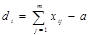 | -2 | -3 | |||
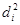 | |||||
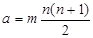 | |||||
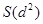 |
В последней строке таблицы 6 указана сумма 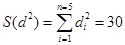 .
.
Для формирования критерия W найдём 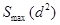 (табл. 7)
(табл. 7)
ТАБЛИЦА 7
| Суммарные ранги для натуральных рядов |  |  | 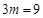 | 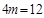 | 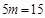 |
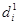 | 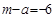 | 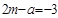 | 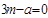 | 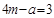 | 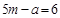 |
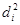 | 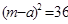 | 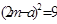 | 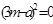 | 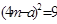 | 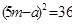 |
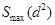 | 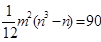 |
Коэффициент W при этом равен
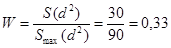
Для оценки значимости коэффициента W используем данные таблицы 4 Приложения [1], где указаны предельные значения сумм Sтабл 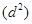 для различных значений m и n при a=0,05. Так, для m=3, n=5 Sтабл
для различных значений m и n при a=0,05. Так, для m=3, n=5 Sтабл 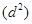 =64.
=64.
Так как 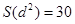 меньше Sтабл
меньше Sтабл 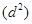 , то гипотеза об отсутствии связи(согласия) подтверждается.
, то гипотеза об отсутствии связи(согласия) подтверждается.
Порядок выполнения работы.
1. Указать факторы, влияющие на бесперебойную подачу электроэнергии на электрической станции.
2. Составить ряды рангов указанных факторов.
3. Применяя различные методы ранговой корреляции проверить гипотезу об отсутствии связи между рядами рангов.
Для этого найти значения коэффициентов t, r для двух произвольно выбранных рядов рангов. Найти коэффициент конкордации W.
Оценить на значимость полученные величины t, r, W и сделать выводы в отношении принятых гипотез.
Результаты исследований представить в виде таблиц 1, 2, 3, 4, 5 и формул (7), (22), (29) (см. «Методические указания»).
Контрольные вопросы.
1. В каких случаях применяют метод ранжирования переменных?
2. Как записывается формула для коэффициента ранговой корреляции Г и каковы пределы его измерения? Что означает, если Г=0, +1, -1?
3. Как проверяется на значимость коэффициент ранговой корреляции t?
4. Каков смысл коэффициента конкордации W?
5. Как оценивается величина W на значимость?
Приложение.
Вероятность того, что данная величина S (для t) будет достигнута или превышена
Таблица 1
| S | n | S | n | |||||
| 0,625 | 0,592 | 0,548 | 0,540 | 0,500 | 0,500 | 0,500 | ||
| 0,375 | 0,408 | 0,452 | 0,460 | 0,360 | 0,386 | 0,431 | ||
| 0,167 | 0,242 | 0,360 | 0,381 | 0,235 | 0,281 | 0,364 | ||
| 0,042 | 0,117 | 0,274 | 0,306 | 0,136 | 0,191 | 0,300 | ||
| 0,042 | 0,199 | 0,238 | 0,068 | 0,119 | 0,242 | |||
| 0,0083 | 0,138 | 0,179 | 0,028 | 0,068 | 0,190 | |||
| 0,089 | 0,130 | 0,0083 | 0,035 | 0,146 | ||||
| 0,054 | 0,090 | 0,0014 | 0,015 | 0,108 | ||||
| 0,031 | 0,060 | 0,0054 | 0,078 | |||||
| 0,016 | 0,038 | 0,0014 | 0,054 | |||||
| 0,0071 | 0,022 | 0,00020 | 0,036 | |||||
| 0,0028 | 0,012 | 0,023 | ||||||
| 0,00087 | 0,0063 | 0,014 | ||||||
| 0,00019 | 0,0029 | 0,0083 | ||||||
| 0,000025 | 0,0012 | 0,0046 | ||||||
| 0,00043 | 0,0023 | |||||||
| 0,00012 | 0,0011 | |||||||
| 0,000025 | 0,00047 | |||||||
| 0,0000028 | 0,00018 | |||||||
| 0,000058 | ||||||||
| 0,000015 | ||||||||
| 0,0000028 | ||||||||
| 0,00000028 |
Вероятность возникновения данной (или меньшей) величины S(d2)
(для r)
Таблица 2
| n=4 | n=5 | n=6 | n=7 | n=8 | n=9 | n=10 |
| S(d2) P | S(d2) P | S(d2) P | S(d2) P | S(d2) P | S(d2) P | S(d2) P |
| 10 0,542 | 20 0,525 | 34 0,500 | 56 0,518 | 84 0,512 | 120 0,509 | 164 0,500 |
| 8 0,458 | 18 0,475 | 32 0,460 | 54 0,482 | 82 0.488 | 118 0,491 | 162 0,486 |
| 6 0,375 | 16 0,392 | 30 0,401 | 52 0,453 | 80 0,467 | 116 0,474 | 160 0,473 |
| 4 0,208 | 14 0,342 | 28 0,357 | 50 0,420 | 78 0,411 | 114 0,455 | 158 0,459 |
| 2 0,167 | 12 0,258 | 26 0,320 | 48 0,391 | 76 0,420 | 112 0,440 | 156 0,446 |
| 0 0,042 | 10 0,225 | 24 0,282 | 46 0,357 | 74 0,397 | 110 0,422 | 154 0,433 |
| 8 0,175 | 22 0,249 | 44 0,331 | 72 0,376 | 108 0,405 | 152 0,419 | |
| 6 0,117 | 20 0,210 | 42 0,297 | 70 0,352 | 106 0,388 | 150 0,406 | |
| 4 0,067 | 18 0,178 | 40 0,278 | 68 0,332 | 104 0,372 | 148 0,393 | |
| 2 0,042 | 16 0,149 | 38 0,249 | 66 0,310 | 102 0,354 | 146 0,379 | |
| 8 0,012 | 36 0,076 | 71 0,146 | 116 0,203 | |||
| 6 0,0062 | 34 0,066 | 70 0,0135 | 114 0,193 | |||
| 4 0,0034 | 32 0,057 | 68 0,125 | 112 0,184 | |||
| 2 0,0014 | 30 0,048 | 66 0,0115 | 110 0,174 | |||
| 0 0,00020 | 28 0,042 | 64 о,10б | 108 0,165 | |||
| 26 0,035 | 62 0,097 | 106 0,156 | ||||
| 24 0,029 | 60 0,0b9 | 104 0,148 | ||||
| 22 0,023 | 58 0,081 | 102 0,139 | ||||
| 20 0,018 | 56 0,074 | 100 0,132 | ||||
| 18 0,014 | 54 0,066 | 98 0,124 | ||||
| 16 0,011 | 52 0,060 | 96 0,116 | ||||
| 14 0,0077 | 50 0,054 | 94 0,109 | ||||
| 12 0,0054 | 48 0,048 | 92 0,102 | ||||
| 10 0,0036 | 46 0,043 | 90 0,096 | ||||
| 8 0,0023 | 44 0,038 | 88 0,089 | ||||
| 6 0,0011 | 42 0,033 | 86 0,083 | ||||
| 4 0,00057 | 40 0,029 | 84 0,077 | ||||
| 2 0,00020 | 38 0,025 | 82 0,072 | ||||
| 0 0,000025 | 36 0.022 | 80 0,06 | ||||
| 34 0.018 | 78 0,062 | |||||
| 32 0,016 | 76 0,057 | |||||
| 30 0,013 | 74 0.052 | |||||
| 28 0.011 | 72 0,048 | |||||
| 26 0,0086 | 70 0,044 | |||||
| 24 0,0069 | 68 0,040 | |||||
| 22 0,0054 | 66 0,037 | |||||
| 20 0,0041 | 64 0,033 | |||||
| 18 0,0030 | 62 0,030 | |||||
| 16 0,0022 | 60 0,027 | |||||
| 14 0,0055 | 58 0,025 | |||||
| 12 0,0010 | 56 0,022 | |||||
| 10 0,00066 | 54 0,019 | |||||
| 8 0,00037 | 52 0,017 | |||||
| 6 0,00018 | 50 0,015 | |||||
| 4 0,000083 | 48 0,013 | |||||
| 2 0,000025 | 46 0,012 | |||||
| 0 0,0000028 | 44 0,010 | |||||
| 42 0,0087 | ||||||
| 40 0,0075 | ||||||
| 38 0,0073 | ||||||
| 36 0,0053 | ||||||
| 34 0,0044 | ||||||
| 32 0,0036 | ||||||
| 31 0,0029 | ||||||
| 28 0.0024 | ||||||
| 26 0,0019 | ||||||
| 24 0,0014 | ||||||
| 22 0,0011 | ||||||
| 20 0,00080 | ||||||
| 18 0,00057 | ||||||
| 16 0,00040 | ||||||
| 14 0,00027 | ||||||
| 12 0,00017 | ||||||
| 10 0,00010 | ||||||
| 8 0,000054 | ||||||
| 6 0,000025 | ||||||
| 4 0,000010 | ||||||
| 2 0,0000028 | ||||||
| 0,00000028 |
Коэффициент конкордации
Вероятность того, что, данная величина S будет достигнута или превышена
(для n=3)
Таблица За
| S | |||||||||
| 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | |
| 0,833 | 0,944 | 0,931 | 0,954 | 0,956 | 0,964 | 0,967 | 0,971 | 0,974 | |
| 0,500 | 0,528 | 0,653 | 0,691 | 0,740 | 0,768 | 0,794 | 0,814 | 0,8о0 | |
| 0,167 | 0,361 | 0,431 | 0,522 | 0,570 | 0.620 | 0,654 | 0.685 | 0,710 | |
| 0,194 | 0,273 | 0,367 | 0,430 | 0,486 | 0,531 | 0,569 | 0,601 | ||
| 0,028 | 0,125 | 0,182 | 0,252 | 0,305 | 0,355 | 0,398 | 0,436 | ||
| 0,069 | 0,124 | 0,184 | 0,237 | 0,285 | .,328 | 0,368 | |||
| 0,042 | 0,093 | 0,142 | 0,192 | 0.236 | 0,278 | 0,316 | |||
| 0,0046 | 0,039 | 0,072 | 0.112 | 0,149 | 0,187 | 0,222 | |||
| 0,024 | 0,052 | 0,085 | 0,120 | 0,154 | 0,187 | ||||
| 0,0085 | 0,029 | 0,051 | 0,079 | 0,107 | 0,135 | ||||
| 0,00077 | 0,012 | 0,027 | 0,047 | 0,069 | 0,092 | ||||
| 0,00я1 | 0,021 | 0.038 | 0.057 | 0,078 | |||||
| 0,0055 | 0,016 | 0,030 | 0 048 | 0,066 | |||||
| 0,0017 | 0,0084 | 0,018 | 0,031 | 0.046 | |||||
| 0,0001 | 0,0036 | 0,0099 | 0.019 | 0,0£0 | |||||
| 0,0027 | 0,0080 | 0,016 | 0,026 | ||||||
| 0,0012 | 0,0048 | 0.010 | 0,018 | ||||||
| 0,00032 | 0,0024 | 0,0060 | 0.012 | ||||||
| 0,00032 | 0,0011 | 0,0035 | 0,0075 | ||||||
| 0,000021 | 0,00086 | 0,0029 | 0,0063 | ||||||
| 0,00026 | 0,0013 | 0,0034 | |||||||
| 0,000061 | 0,00066 | 0,0020 | |||||||
| 0,000061 | 0,00035 | 0,0013 | |||||||
| 12J | 0.000061 | О.ОС020 | 0,00083 | ||||||
| 0,0000036 | 0,000097 | 0,00051 | |||||||
| 0,000054 | 0,00037 | ||||||||
| 0,000011 | 0,00018 | ||||||||
| 0,000011 | 0,00011 | ||||||||
| 0,000011 | 0,000085 | ||||||||
| 0,000011 | 0,000044 | ||||||||
| 0,0000060 | 0,000020 | ||||||||
| 0,000011 | |||||||||
| 0,0000021 | |||||||||
| 0,000000099 |
Коэффициент конкордации
Вероятность того, что данная величина S будет достигнута или превышена
(для п = 4)
Таблица 3b
| S | m=З | m=5 | S | m=5 |
| 1.000 | 1.000 | 0,055 | ||
| 0,958 | 0,975 | 0,044 | ||
| 0,910 | 0,944 | 0.034 | ||
| 0,727 | 0,857 | 0,031 | ||
| 0.108 | 0,771 | 0,023 | ||
| 0,524 | 0,709 | 0,020 | ||
| 0,446 | 0,652 | 0,017 | ||
| 0,342 | 0.561 | 0,012 | ||
| 0,300 | 0,521 | 0,0087 | ||
| 0,207 | 0,445 | 0,0067 | ||
| 0,175 | 0,408 | 0,0055 | ||
| 0,148 | 0,372 | 0.0031 | ||
| 0,075 | 0,298 | 0,0023 | ||
| 0,054 | 0,260 | 0,0018 | ||
| 0,033 | 0,226 | 0,0016 | ||
| 0,017 | 0,210 | 0,0014 | ||
| 0,0017 | 0,162 | 0,00064 | ||
| 0,0017 | 0,141 | 0,00043 | ||
| 0,123 | 0,00021 | |||
| 0,107 | 0,00014 | |||
| 0,093 | 0,000048 | |||
| 0.075 | 0,0000030 | |||
| 0,067 |
Коэффициент конкордации
Вероятность того, что данная величина 5 будет достигнута или превышена
(для п = 4)
Таблица 3с
