Соотношения между прямой и двойственной задачами ЛП

Для симметричной пары задач двойственная задача по отношению к прямой составляется по следующим правилам:

1) Число переменных в двойственной задаче равно числу ограничений в прямой задаче.

2) Матрица коэффициентов системы ограничений двойственной задачи получается из матрицы коэффициентов системы ограничений прямой задачи путём транспонирования.

3) Система ограничений двойственной задачи записывается в виде неравенств противоположного смысла неравенствам системы ограничений прямой задачи.

4) Свободными членами системы ограничений двойственной задачи являются коэффициенты функции цели прямой задачи.

5) На каждую переменную двойственной задачи накладывается условие неотрицательности.

6) Двойственная задача решается на минимум, если целевая функция прямой задачи задается на максимум,и наоборот..

7) Коэффициентами функции цели двойственной задачи служат свободные члены системы ограничений прямой задачи.

8) Для основной задачи ЛП и двойственной к ней задачи справедливы следующие теоремы.

Теорема 1. Если одна из пары двойственных задач ЛП имеет решение, то и другая задача имеет решение, причём значения целевых функций этих задач равны, т.е. .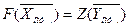

Теорема 2. Произвольное допустимое базисное решение одной задачи из пары двойственных задач оптимально тогда и только тогда, когда система ограничений двойственной задачи совместна.

Теорема 3. Если целевая функция одной из пары двойственных задач неограниченна снизу(сверху), то система ограничений другой задачи этой пары несовместна.

9) Зная решение одной задачи из пары двойственных задач, можно, не решая вторую задачу, найти её решение, которое получается из соответствия основных и дополнительных переменных этих двух задач.

Сопряжённые пары:

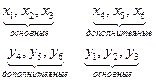
Решение прямой задачи даёт оптимальные объёмы в структуру товарооборота предприятия, а решение двойственной – оптимальную систему оценок ресурсов, используемых для реализации товаров.

Пример решения двойственной задачи ЛП.

Пример. Составим двойственную задачу к прямой задаче, которая решена симплексным методом в пункте 3.2.

Определить 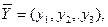который удовлетворяет условиям-ограничениям:

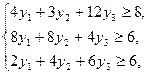
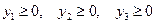и обеспечивает минимальное значение целевой функции

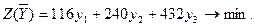
Используя схему перевода переменных прямой и двойственной задачи, получим оптимальный план

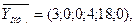
при этом

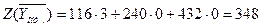тыс.руб.

По этим данным проводится анализ оптимального плана двойственной задачи по оценке ресурсов, используемых для реализации товаров.

Тема 5.Транспортная задача.