Проверка соответствия уравнения регрессии экспериментальному материалу.
Процедура проверки соответствия установленной зависимости экспериментальному материалу (проверка адекватности) включает три этапа.
Первый. Ищется остаточная дисперсия или дисперсия адекватности
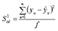
Здесь yu - экспериментальное значение выходной величины для соответствующего значения xu;
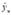 - рассчитанное по уравнению регрессии значение функции для данного xu;
- рассчитанное по уравнению регрессии значение функции для данного xu;
n – число опытов;
f = n-l – число степеней свободы;
l – число коэффициентов в уравнении регрессии.
Уже по 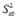 можно судить о степени соответствия уравнения экспериментальному материалу. Ведь
можно судить о степени соответствия уравнения экспериментальному материалу. Ведь 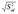 - среднеквадратическое отклонение экспериментальных точек от значений, полученных по уравнению.
- среднеквадратическое отклонение экспериментальных точек от значений, полученных по уравнению.
Второй. Определяется дисперсия воспроизводимости
На каждом уровне аргумента xu проводится несколько параллельных опытов, ищутся дисперсии для каждой группы экспериментов, проверяется их однородность и затем определяется средневзвешенная дисперсия 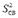 . Она и является дисперсией воспроизводимости
. Она и является дисперсией воспроизводимости 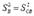 .
.
Если параллельные опыты не проводятся, то в качестве средневзвешенной дисперсии принимается
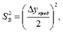
где 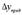 – предельная абсолютная ошибка в определении входной величины.
– предельная абсолютная ошибка в определении входной величины.
С доверительной вероятностью 0,955 можно считать предельную ошибку, равной 
Третий. Поверяется однородность дисперсий адекватности и воспроизводимости.
Если расчетное значение критерия Фишера окажется меньше табличного, то полученное уравнение регрессии адекватно эксперименту
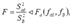
где 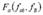 – берется из таблиц с учетом принятого уровня значимости для соответствующих степеней свободы
– берется из таблиц с учетом принятого уровня значимости для соответствующих степеней свободы 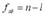 и
и 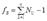 .
.
Здесь Nu- число параллельных опытов на каждом уровне аргумента.
26. Приближённая интеграция диф уравнений.
Приближенными называют методы, в которых решение получается как предел некоторой последовательности функций, причем каждый член этой последовательности выражается через элементарные функции или квадратуры. Эти методы удобны, когда большую часть промежуточных выкладок удается осуществить точно
Многие способы приближенного решения дифференциальных уравнений основаны на методах доказательства теоремы существования и единственности. Например, метод разложения решения в степенной ряд позволяет найти несколько первых членов ряда Тейлора для искомого решения, что дает хорошее приближение для этого решения вблизи точки х0.
Для приближенного интегрирования дифференциальных уравнений можно воспользоваться степенными рядами либо в виде ряда Маклорена
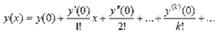 , (13)
, (13)
либо в виде ряда 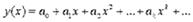 (14)
(14)
с неопределенными коэффициентами.
При интегрировании нелинейных дифференциальных уравнений удобнее пользоваться рядом (13). Варианту (14) отдается предпочтение при интегрировании линейных дифференциальных уравнений.
Применение ряда Тейлора состоит в следующем. Записав решение дифференциального уравнения в виде ряда Тейлора, пользуемся самим уравнением и заданными начальными условиями для определения производных от искомой функции, которые затем подставляют в решение.
