Заимодействие струй с преградой
урбулентные струи
2.4.1. Общие свойства
Струйное течение характеризуется тангенциальными разрывами в параметрах: скорости, плотности, температуры и концентрации. Статическое давление при этом не претерпевает разрыва.
Поверхность тангенциального разрыва в силу действия диффузии, а также гидродинамической неустойчивости (начальное возмущение в виде выступа или впадины границы струи будет увеличиваться вниз по потоку), теряет устойчивость. В результате этого будут возникать вихревые течения согласно схеме рис.2.21.
Эти механизмы приводят к обмену количествами движения высокоскоростных частиц струи с неподвижными во внешней среде и к вихревым образованиям, размер которых увеличивается вниз по потоку в стороны неподвижной и движущейся среды. При этом потенциальное ядро на длине участка, называемого начальным, исчезает, и начинается падение начальной скорости  до
до 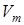 (максимальной на оси струи). Схема турбулентной струи представлена на рис.2.22.
(максимальной на оси струи). Схема турбулентной струи представлена на рис.2.22.

Рис.2.21. Схема роста начального возмущения и потеря
устойчивости границы струи

Рис.2.22. Схема течения осесимметричной струи
В сторону неподвижной среды струя распространяется до границы 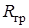 . Эта область называется струйным турбулентным пограничным слоем. При очень малых числах
. Эта область называется струйным турбулентным пограничным слоем. При очень малых числах 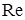 некоторый участок свободной струи может быть ламинарным, то есть слоистым по структуре течения. Однако свободная граница струи (отсутствие стенок) определяет разрушение границы и турбулентный характер течения. Закон распределения скорости в поперечных сечениях струи соответствует закону распределения в турбулентном пограничном слое (профиль Шлихтинга):
некоторый участок свободной струи может быть ламинарным, то есть слоистым по структуре течения. Однако свободная граница струи (отсутствие стенок) определяет разрушение границы и турбулентный характер течения. Закон распределения скорости в поперечных сечениях струи соответствует закону распределения в турбулентном пограничном слое (профиль Шлихтинга):
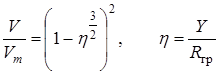 .
.
Как и для пограничного слоя, важными свойствами турбулентной струи для составления схемы расчета являются: постоянство давления в поперечных сечениях и малость поперечных скоростей по сравнению с продольными. Имеются обширные экспериментальные и теоретические исследования турбулентных струй.
В качестве основных направлений по созданию математических моделей течения, помимо современных численных методов расчета струй, упомянутых выше в разделе 2.1, можно отметить следующие.
1. Теория Толмина, в основе которой лежит гипотеза Прандтля о постоянстве в каждом сечении пути смешения частиц движущегося потока со средой, вследствие чего имеет место линейное нарастание турбулентного пограничного слоя (  ).
).
В пределах длины пути смешения наблюдаются, по данным измерений, одинаковые значения мгновенных скоростей частиц. Размеры вихрей пропорциональны путям смешения.
2. Теория Рейхардта, основанная на описании процесса смешения уравнениями теплопроводности (асимптотическая граница струи).
3. Теория на основе статистических зависимостей.
Все методики требуют использования эмпирических констант. Наиболее наглядное представление свойств турбулентных струй дает нам первое направление. Возьмем зависимости, рекомендованные Г.Н. Абрамовичем для схемы течения осесимметричной струи, представленной на рис.2.22.
2.4.2. Методика расчета турбулентной струи
Струя считается истекающей из точки – полюса 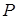 , отнесенного от среза сопла на расстояние
, отнесенного от среза сопла на расстояние 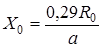 потенциальный участок имеет протяженность
потенциальный участок имеет протяженность  . Граница струи определяется по формуле:
. Граница струи определяется по формуле:  , где
, где 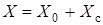 – расстояние сечений струи от "полюса".
– расстояние сечений струи от "полюса".
В пределах этой границы проводится интегрирование зависимостей распределения по сечению струи количества движения и энергии элементарных масс смеси газов с воздухом:
 .
.
В соответствии со схемой и изложенными условиями (постоянство давления по сечениям, линейность границы струи и др.) можно написать следующие уравнения сохранения импульса и избыточного теплосодержания струи во всех сечениях с учетом присоединения к ней массы воздуха:
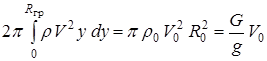 ; (2.12)
; (2.12)
 . (2.13)
. (2.13)
По решению Толмина при  в холодной струе устанавливается следующая связь между безразмерной скоростью и безразмерным расстоянием по оси струи, показывающая на линейное падение скорости
в холодной струе устанавливается следующая связь между безразмерной скоростью и безразмерным расстоянием по оси струи, показывающая на линейное падение скорости 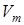 c расстоянием
c расстоянием 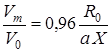 . Темп падения зависит от константы турбулентности
. Темп падения зависит от константы турбулентности  .
.
Получение значений эмпирических констант является одной из основных задач экспериментов. Было установлено, что дозвуковое течение более интенсивно перемешивается с неподвижным воздухом, чем сверхзвуковое. Поэтому в расчетах принимается:
· для дозвука  ;
;
· для сверхзвука  .
.
В горячей струе с начальным подогревом 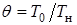 падение скорости по оси будет более интенсивным, чем у холодной, что видно из следующей зависимости в неявной форме:
падение скорости по оси будет более интенсивным, чем у холодной, что видно из следующей зависимости в неявной форме:
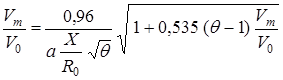 . (2.14)
. (2.14)
Имеется следующая связь между безразмерными скоростью и температурой:
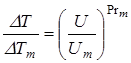 ,
,
где 
Турбулентное число Прандтля
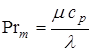 .
.
Из "интерполяционной формулы" (2.14) следует, что струя с  теряет скорость быстрее, чем при
теряет скорость быстрее, чем при  , с удалением от среза сопла приблизительно пропорционально
, с удалением от среза сопла приблизительно пропорционально 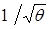 , то есть она менее "дальнобойная".
, то есть она менее "дальнобойная".
В практике частым случаем является действие струй многосопловых двигательных установок. Совместное действие турбулентных составных газовых струй определяется суммированием удельных количеств движения и избыточных теплосодержаний в общих точках полей распределения параметров каждой струи (  ,
, 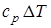 ).
).
По значению 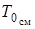 (смеси) можно определить коэффициент подмешивания воздуха в каждой точке
(смеси) можно определить коэффициент подмешивания воздуха в каждой точке  , так как
, так как 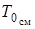 однозначно связана с
однозначно связана с  .
.
По 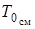 можно определить плотность
можно определить плотность  , так как
, так как 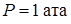 .
.
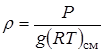 ;
;
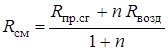 ;
;
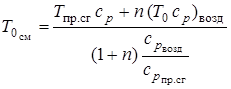 ;
;
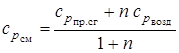 .
.
заимодействие струй с преградой
2.5.1. Определение критического угла при отражении струи от наклонной плоскости
Несжимаемая плоская струя
Схема натекания несжимаемой плоской струи на преграду под углом 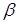 к оси струи представлена на рис.2.23.
к оси струи представлена на рис.2.23.
Уравнения сохранения:
· массы: 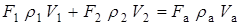 ;
;
· импульса:  ;
;

 .
.

Рис.2.23. Схема натекания несжимаемой плоской струи на преграду
Отсюда 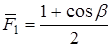 ;
;
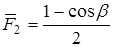 .
.
Векторы количества движения  , прямого и обратного течения на преграде
, прямого и обратного течения на преграде 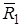 и
и 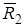 находятся в равновесии с силой реакции преграды
находятся в равновесии с силой реакции преграды 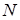 (см. схему на рис.2.23). При угле наклона преграды
(см. схему на рис.2.23). При угле наклона преграды  должно обеспечиваться
должно обеспечиваться  и
и 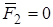 . Это будет выполняться только из условия
. Это будет выполняться только из условия 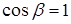 при
при  . То есть несжимаемая плоская струя критического угла не имеет.
. То есть несжимаемая плоская струя критического угла не имеет.
Сжимаемая плоская струя
Уравнения сохранения будут аналогичны, однако при условии  будет
будет
 ;
;
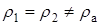 .
.
Так как  , то
, то 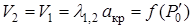 . Поскольку
. Поскольку 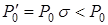 , то
, то 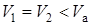 .
.
Тогда
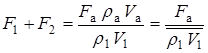 ,
,
где 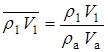 ;
;
 ,
,
где 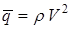 ;
;
 ;
;
 ;
; 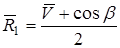 ;
;
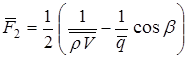 ;
;  .
.
При полном отражении 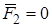 ,
, 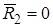 и
и 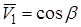 .
.
Для обеспечения 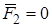 должно быть:
должно быть:  .
.
Так как в сжимаемом потоке  , то для плоского сжимаемого потока будет существовать
, то для плоского сжимаемого потока будет существовать  . Это условие реализуется из-за уменьшения скорости стекающего потока и его количества движения. Значение критического угла можно определить, зная величину потерь полного давления за скачками на преграде (
. Это условие реализуется из-за уменьшения скорости стекающего потока и его количества движения. Значение критического угла можно определить, зная величину потерь полного давления за скачками на преграде ( 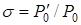 ):
):
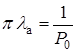 ;
;
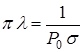 ;
;
 ,
,
или 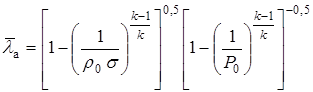 .
.
Условие полного отражения сжимаемого потока может быть реализовано при присоединенном косом скачке (рис.2.24). Значение, при котором скачок будет отходить от преграды, можно определить с помощью ударной поляры.

Рис.2.24. Присоединенный скачок и образование обратного течения
при отошедшем скачке
Для этого рассмотрим графическое построение косого скачка для натекания потока со скоростью  , при известной величине натекания
, при известной величине натекания  на преграду с углом
на преграду с углом 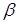 . Эпюра скоростей на косом скачке представлена на рис.2.25. Поляра дает значение вектора
. Эпюра скоростей на косом скачке представлена на рис.2.25. Поляра дает значение вектора  после скачка как при регулярном отражении скачка
после скачка как при регулярном отражении скачка  при угле клина
при угле клина 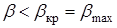 , так и при отошедшем скачке, включая косой скачок.
, так и при отошедшем скачке, включая косой скачок.
Направим ось  по линии вектора
по линии вектора  . Построим в плоскости годографа скорости
. Построим в плоскости годографа скорости  линию
линию 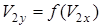 . Обозначим для упрощения записи
. Обозначим для упрощения записи 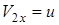 и
и 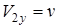 .
.
Для прямого скачка имеет соотношения для скоростей до и после скачка  .
.

Рис.2.25. Эпюра скоростей на косом скачке
При построении поляры для течения с косым скачком  рассматриваются тангенциальная
рассматриваются тангенциальная  и нормальная составляющие
и нормальная составляющие 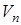 скорости
скорости  набегающего потока к фронту скачка. Для нормальных составляющих к фронту скачка используется соотношение, имеющее место при прямом скачке:
набегающего потока к фронту скачка. Для нормальных составляющих к фронту скачка используется соотношение, имеющее место при прямом скачке:
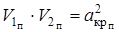 ,
,
где  – скорость звука частичного торможения.
– скорость звука частичного торможения.
Скорость  определяется из критической скорости потока за вычетом эффекта торможения тангенциальной составляющей:
определяется из критической скорости потока за вычетом эффекта торможения тангенциальной составляющей:
 .
.
Это соотношение следует из уравнения энергии, учитывающего отсутствие энергии торможения от составляющей 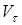 :
:
 ,
,
где  – температура частичного торможения.
– температура частичного торможения.
Одновременно
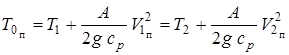 ,
,
где 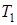 ,
, 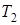 – статическая температура потока до и после скачка. Порядок построения (графического) ударной поляры приведен ниже.
– статическая температура потока до и после скачка. Порядок построения (графического) ударной поляры приведен ниже.
Для нахождения искомой зависимости используем основное уравнение косого скачка
 .
.
Подставив в это уравнение значения 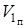 и
и 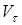 из соотношений (см. рис.2.25)
из соотношений (см. рис.2.25)

находим

так как (см. рис.2.25) 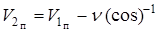 .
.
Преобразуем полученное уравнение к виду
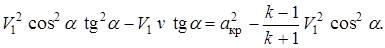
Отсюда, полагая, что 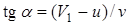 , получаем
, получаем
 .
.
Полученное уравнение в плоскости 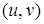 описывает кривую второго порядка, симметричную относительно оси
описывает кривую второго порядка, симметричную относительно оси  , называемую гипоциссоидой (рис.2.26) – ударной полярой.
, называемую гипоциссоидой (рис.2.26) – ударной полярой.
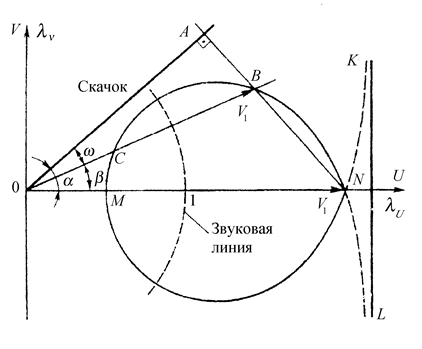
Рис.2.26. Ударная поляра
Как видно из уравнения ударной поляры,  либо в том случае, если
либо в том случае, если 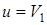 , либо если
, либо если  . Первый случай соответствует точке
. Первый случай соответствует точке 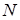 (см. рис.2.26), или бесконечно малому возмущению (волна Маха); второй случай соответствует точке
(см. рис.2.26), или бесконечно малому возмущению (волна Маха); второй случай соответствует точке 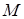 – прямому скачку уплотнения. Бесконечные ветви ударной поляры, начальные участки которых
– прямому скачку уплотнения. Бесконечные ветви ударной поляры, начальные участки которых  и
и  имеют асимптоту, соответствующую значению
имеют асимптоту, соответствующую значению 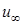 , при котором третья скобка уравнения ударной поляры обращается в нуль; при этом
, при котором третья скобка уравнения ударной поляры обращается в нуль; при этом  ,
,
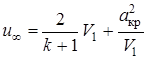 .
.
Как видно из рис.2.26, на этих ветвях  ; они соответствуют скачкам разрежения и, следовательно, физически не реализуются. Замкнутая же часть ударной поляры отвечает скачкам уплотнения: здесь
; они соответствуют скачкам разрежения и, следовательно, физически не реализуются. Замкнутая же часть ударной поляры отвечает скачкам уплотнения: здесь 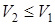 .
.
Возьмем на ударной поляре некоторую произвольную точку  ; ей соответствует вектор скорости
; ей соответствует вектор скорости  .Восстанавливая к
.Восстанавливая к 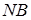 перпендикуляр из точки
перпендикуляр из точки 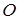 , найдем направление фронта скачка уплотнения
, найдем направление фронта скачка уплотнения  . На рис.2.26 штрихами нанесена также окружность радиуса
. На рис.2.26 штрихами нанесена также окружность радиуса 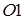 (скорость звука набегающего потока).
(скорость звука набегающего потока).
Таким образом, при заданном показателе адиабаты 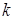 можно построить серию ударных поляр, различающихся лишь положением точки
можно построить серию ударных поляр, различающихся лишь положением точки 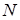 , то есть величиной скорости
, то есть величиной скорости  . Для расчета точек ударной поляры уравнение ударной поляры целесообразно преобразовать к безразмерной форме, введя
. Для расчета точек ударной поляры уравнение ударной поляры целесообразно преобразовать к безразмерной форме, введя 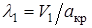 ,
,  ,
, 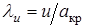 . При этом уравнение ударной поляры примет вид
. При этом уравнение ударной поляры примет вид
 .
.
График на рис.2.26 построен на базе расчетов, проведенных по полученной формуле для  и
и  . Количественную информацию из этого рисунка можно получить, если положить
. Количественную информацию из этого рисунка можно получить, если положить  и
и 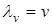 .
.
С помощью ударной поляры удобно решать различные простейшие задачи с косыми скачками уплотнения. Пусть, например, задан угол наклона преграды  , обтекаемого потоком со скоростью
, обтекаемого потоком со скоростью  . Через точку
. Через точку 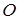 проводим под углом
проводим под углом 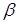 луч
луч  , пересекающий ударную поляру в точках
, пересекающий ударную поляру в точках  и
и 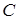 , каждая из которых отвечает одному из двух возможных значений скоростей
, каждая из которых отвечает одному из двух возможных значений скоростей  и направлений скачка уплотнения. Так, для большей скорости
и направлений скачка уплотнения. Так, для большей скорости  :
:  – направление фронта скачка
– направление фронта скачка  . Аналогично этому можно найти и направление фронта скачка для второго дозвукового значения скорости
. Аналогично этому можно найти и направление фронта скачка для второго дозвукового значения скорости  .
.
Отметим, что, как правило, одно значение  – сверхзвуковое, а другое всегда дозвуковое. Каждое из этих значений
– сверхзвуковое, а другое всегда дозвуковое. Каждое из этих значений  определяет свое давление
определяет свое давление 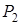 за скачком. Как видно из рис.2.26, существует значение
за скачком. Как видно из рис.2.26, существует значение 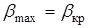 , соответствующее касанию вектора
, соответствующее касанию вектора  к ударной поляре. При
к ударной поляре. При 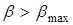 косой скачок существовать не может, и перед преградой образуется отошедший от преграды прямой скачок уплотнения (рис.2.24).
косой скачок существовать не может, и перед преградой образуется отошедший от преграды прямой скачок уплотнения (рис.2.24).
Если задано значение  – точка
– точка 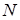 и направление косого скачка уплотнения
и направление косого скачка уплотнения  ,то, восстанавливая к
,то, восстанавливая к  из точки
из точки 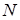 перпендикуляр, найдем точку
перпендикуляр, найдем точку  как пересечение
как пересечение  с ударной полярой.
с ударной полярой.
Влияние растекания струи по преграде на величину критического угла отражателя 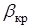
Если явление сжимаемости уменьшает вектор количества движения струи  пропорционально
пропорционально 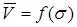 , то растекание струи в стороны под углом
, то растекание струи в стороны под углом 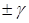 по преграде тоже приводит к уменьшению вектора
по преграде тоже приводит к уменьшению вектора  . Это уменьшение можно оценивать отношением суммы проекций количества движения элементарных струй на ось
. Это уменьшение можно оценивать отношением суммы проекций количества движения элементарных струй на ось 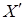 к количеству движения исходной струи, приняв
к количеству движения исходной струи, приняв  , то есть без учета сжимаемости. Если представить схему течения струи на пластине с полюсом растекания
, то есть без учета сжимаемости. Если представить схему течения струи на пластине с полюсом растекания 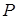 согласно рис.2.27-a, то при растекании струи по преграде с критическим углом
согласно рис.2.27-a, то при растекании струи по преграде с критическим углом 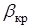 полюс
полюс 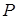 будет располагаться в верхней части проекции на преграду границы струи (рис.2.27-б).
будет располагаться в верхней части проекции на преграду границы струи (рис.2.27-б).
Согласно схеме, проекция вектора  на ось
на ось 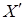 будет
будет 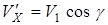 . Элементарный расход массы через сечение струи
. Элементарный расход массы через сечение струи 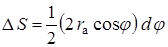 будет
будет 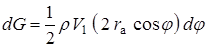 . Проекция единичного вектора количества движения на ось
. Проекция единичного вектора количества движения на ось 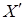 будет
будет
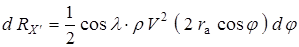 .
.
Тогда, учитывая геометрические соотношения (рис.2.27-б), получим
 .
.
Поскольку при полном отражении будет иметь место
 ,
,
то  .
.
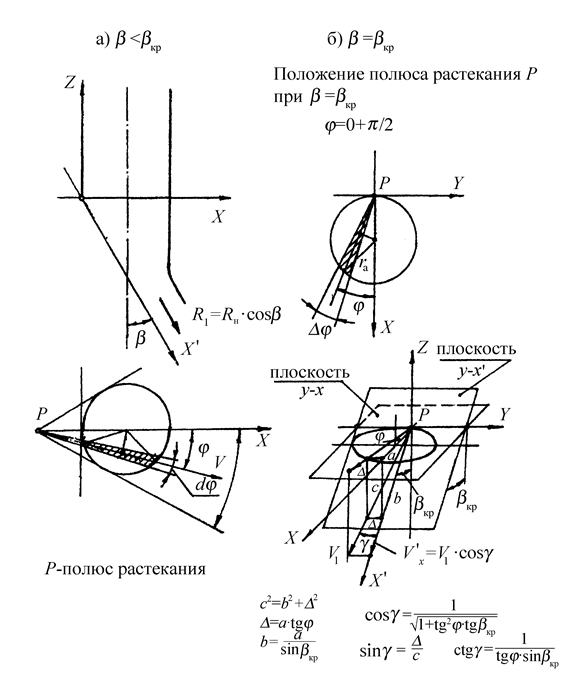
Рис.2.27. Схема растекания струи по преграде в зависимости от угла 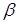
Интегрируя и подставляя пределы, получим
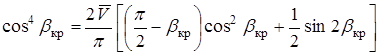 ,
,
где 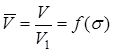 – функция волновых потерь скорости. Значение
– функция волновых потерь скорости. Значение 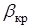 при различных
при различных  можно получить из графика рис.2.28.
можно получить из графика рис.2.28.
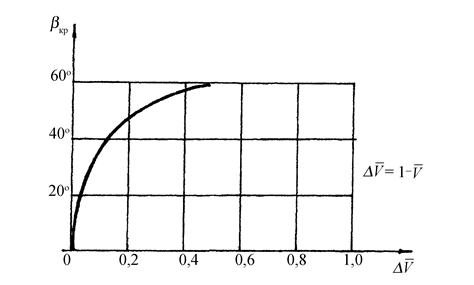
Рис.2.28. Зависимость 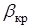 преграды от потерь
преграды от потерь 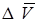 с учетом растекания
с учетом растекания
Как видно из графика для принятой схемы растекания уже при потерях 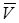 , равных 10%,
, равных 10%, 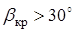 .
.
2.5.2. Воздействие струи на преграду
Течение несжимаемой струи на преграде
Давление струи несжимаемой жидкости на преграду под углом 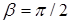 будет
будет 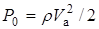 . Радиус пятна струи с количеством движения
. Радиус пятна струи с количеством движения  при законе распределения давления по радиусу пятна
при законе распределения давления по радиусу пятна  будет
будет 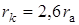 .
.
Это следует из равенства суммарной реакции преграды 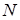 силе тяги струи
силе тяги струи 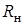 . Реакция
. Реакция 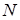 определяется в соответствии с выбранным законом распределения*) давления
определяется в соответствии с выбранным законом распределения*) давления 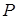 по схеме (рис.2.29).
по схеме (рис.2.29).
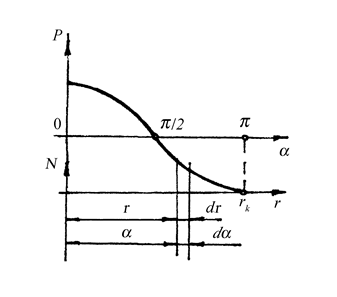
Рис.2.29. Схема распределения давления 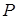 на преграде
на преграде
В таком случае получим:
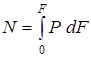 ;
;
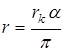 ;
;
 ;
;
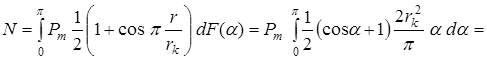
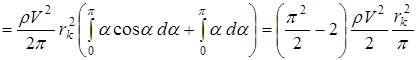 ;
;
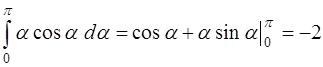 ;
;
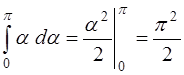 .
.
Таким образом, 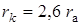 .
.
Течение сжимаемой струи на преграде
Течение сжимаемой струи на преграде определяется закономерностями сверхзвукового пространственного течения со свободной границей в среде с 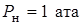 . Схема течения струи представлена на рис.2.30.
. Схема течения струи представлена на рис.2.30.
Для сверхзвуковой струи линия с давлением 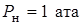 ,
, 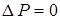 будет на радиусе
будет на радиусе 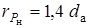 ; сечение с критическими параметрами будет на радиусе
; сечение с критическими параметрами будет на радиусе 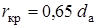 .
.
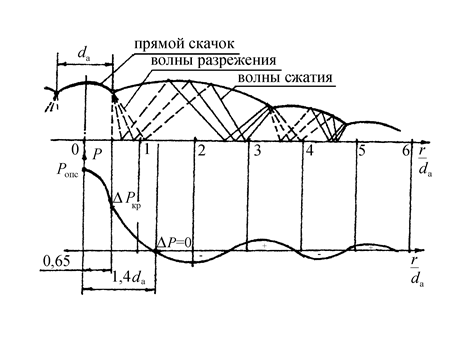
Рис.2.30. Схема течения сжимаемой струи на преграде
В целом давление от сверхзвуковой струи на преграде распределяется сложным образом в силу наличия зон разрежения Прандтль – Майеровского течения и зон уплотнения, аналогично течению струи со свободной поверхностью с синусоидальным распределением амплитуд давления и разрежения с уменьшающимися их максимальными значениями. Можно выделить три кольцевых зоны.
На участке 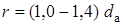 интеграл давления может в 1,3 раза превышать
интеграл давления может в 1,3 раза превышать 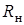 в силу того, что вектор течения на преграде направлен вверх под углом к преграде. На основании схемы течения и экспериментальных данных размер преграды, на которой реализуется полная тяга без колебания давления, будет равен
в силу того, что вектор течения на преграде направлен вверх под углом к преграде. На основании схемы течения и экспериментальных данных размер преграды, на которой реализуется полная тяга без колебания давления, будет равен  .
.
Для нерасчетных струй будет иметь место два режима обтекания: с одним максимумом при расположении преграды в узком сечении и двумя максимумами при расположении в широком сечении.
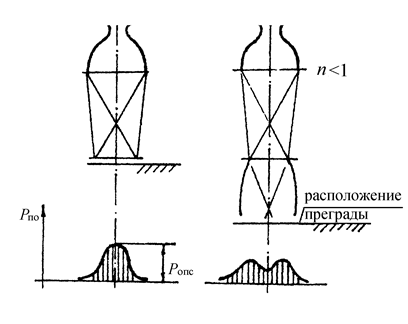
Рис.2.31. Режимы обтекания
Силовое воздействие на бесконечную преграду при  характеризуется полным поворотом потока в направлении плоскости под углом
характеризуется полным поворотом потока в направлении плоскости под углом 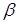 (см. рис.2.23).
(см. рис.2.23).
При этом  ;
;
 ;
;
 ;
;
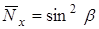 ;
;
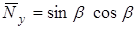 .
.
Из уравнений расхода и импульса получим
 ;
;
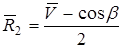 .
.
При  ;
; 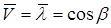 и
и  ;
;
при  *)
*)  .
.
Давление 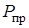 определяется из газодинамического расчета натекающей струи и параметров на преграде за прямым и косым скачками согласно разделу 2.2.7.
определяется из газодинамического расчета натекающей струи и параметров на преграде за прямым и косым скачками согласно разделу 2.2.7.
Силовое воздействие струи на преграду с ограниченными размерами (  ) определяется учетом неполноты
) определяется учетом неполноты  поворота струи в направлении
поворота струи в направлении  (см. рис.2.32).
(см. рис.2.32).
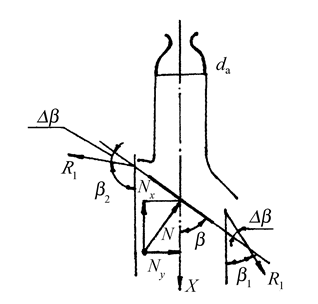

Рис.2.32. Схема натекания струи на плоскость
с ограниченными размерами
В данном случае имеем
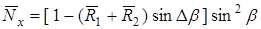 ;
;
 ;
;
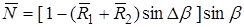 ;
;
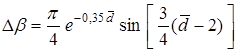 ;
;
 ;
;  ;
;  .
.
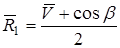 ;
;  при
при 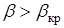 ;
;
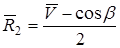 ;
; 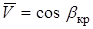 при
при 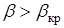 и
и  ;
;
 при
при 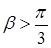 ;
;
 ;
;  при
при 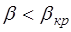 ;
;
при 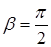 ;
; 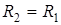 ;
; 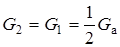 , тогда для
, тогда для 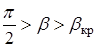 будет линейная зависимость
будет линейная зависимость 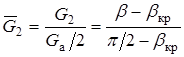 ;
;
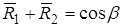 при
при 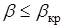 ;
;
 при
при 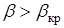 .
.
*) Более точное распределение дают эмпирические зависимости.
*) определяется по ударной поляре.
