Метод последовательной релаксации

Воспользуемся методом Гаусса–Зейделя, записанным в форме

,

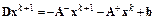или

.

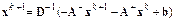Удобная для реализации итерационная схема релаксационного метода имеет вид

,

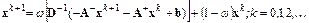где ω – некоторый параметр.

Преобразуем ее к стандартной форме:

.

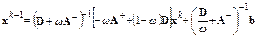В свою очередь итерационная матрица

.

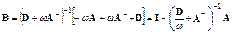В итоге матрица расщепления

.

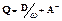При 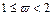указанная итерационная схема соответствует методу последовательной верхней релаксации, при 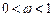– методу последовательной нижней релаксации.

Координатная форма метода последовательной релаксации:

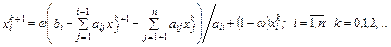
Метод последовательной релаксации для системы с пятидиа-гональной матрицей:

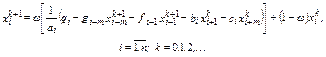
Время выполнения итерации в этом случае

.

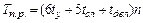Метод касательных.

Метод касательных (Ньютона) применяется для уточнения действительных корней нелинейного уравнения.

Имеем уравнение F(X) = 0. Если F(X) Î D[A, B], и известно F(А) F(В) < 0 (F(А) и F(В) имеют разные знаки) и F¹¹(X) не меняет знака на интервале [А,В], то уравнение F(X) = 0 имеет решение Х^* Î [A, B], F(X^*) º 0.

Процесс уточнения действительного корня нелинейного уравнения методом касательных заключается в том, что строится касательная к кривой F(X) и определяется точка пересечения касательной с осью абсцисс, координата этой точки используется в качестве уточнения корня. Затем к кривой F(X) в точке последнего уточнения корня строят очередную касательную и определяется точка пересечения касательной с осью Х – очередное уточнение корня уравнения. Процесс уточнения корня (построение касательных) продолжается до тех пор пока два ближайших уточнения будут отличаться на величину не более e, точность вычисления корня, | Х_(i) – X_(i-1) | < e

где i - номер итерации..

Ограничение по применению метода. Метод касательных можно применять для уточнения действительного корня, если на интервале [А, В] функция F(X) удовлетворяет следующим свойствам:

интервал [А,В] должен быть достаточно мал, чтобы на его длине график функции F(X) не имел горизонтальных участков, участков с малым наклоном касательных к кривой F(X) и экстремумов, функция F(X) должна быть монотонная, F¹¹(А) F¹¹(В) > 0;

за начальное приближение Х₀ принимается одна из границ интервала [А,В], где F(X) и F¹¹(X) имеют одинаковые знаки, Х₀ = А при условии F(А) F¹¹(А) > 0 (Х₀ = B при условии F(B) F¹¹(B) > 0).

Алгоритм метода.

Исходные данные:

начальное приближение корня Х,

точность вычисления корня e .

Организовать вычисление поправки к уточнению корня, D_Х = F(X) / F¹(X),

Уточнить значение корня. В качестве рекуррентной формулы метода касательных используют формулу вычисления координаты пересечения касательной с осью Х, Х = Х - D_Х,

Проверить условие продолжения уточнения корня, | D_Х | > e .

Если заданное условие принимает значение «истина», то необходимо продолжить уточнение корень уравнения с пункта 2.

Если заданное условие принимает значение «ложно», то корень Х найден с заданной точностью e, организовать вывод значения корня Х и прекратить уточнение корня.

Часть 3. НЕЛИНЕЙНЫЕ АЛГЕБРАИЧЕСКИЕ

УРАВНЕНИЯ И СИСТЕМЫ

Лекция 5