Рямая и двойственная задача

имплексные преобразования

Для того, чтобы завершить шаг преобразований, ведущих к новому опорному плану, в новом базисе выразим новую БП x_j0 из уравнения с номером i₀ системы x_i+∑α_ijj=b_i(j=m+1,n), b_i≥0,i=1,m через СП

x_i0+α_i0,m+1x_m+1+…+α_io,j0-1x_jo-1+α_i0j0x_j0+α_i0,j0+1x_j0+1+…+α_i0nx_n=β_io

x_j0=β_i0/α_i0j0-((α_i0,m+1/α_i0j0)x_m+1+…+ (α_i0,j0-1/α_i0j0)x_j0-1+(1/α_i0j0)x_i0+(α_i0,j0+1/α_i0j0)x_jo+1+…+(α_i0n/α_i0j0)x_n (1)

Аналогично, если мы подставим в выражение (1) в остальные ограничения (1) ограничения и в ЦФ max(min)F=∆₀-∑∆_jx_j(j=m+1), получим след. формулу:

X_i=(β_iα_i0j0-β_i0α_ij0)/α_i0j0-((α_i,m+1α_i0j0-α_i0,m+1α_ij0)/α_i0jo+…-(α_ij0/α_i0j0)x_i0+…+((α_inα_i0j0-α_i0nα_ij0)/α_i0j0)x_n),i=1,m; i≠i₀ (2)

F= (∆₀α_i0j0-∆_j0β_i0)/α_iojo-(((∆_m+1α_i0j0-∆_j0α_i,m+1)/∆_iojo)x_m+1+…-(∆_j0/α_iojo)x_io+…+((∆_nx_iojo-∆_joα_i0n)/α_i0j0)x_n)

Из формул (1)-(3) следуют правила пересчета элементов таблиц:

1)из выражения (1) следует, что элемент новой таблицы, стоящий на месте разрешающего , заменяется обратной величиной.

2)из выражения (1) следует, что оставшиеся элементы разрешающей строки i₀ новой таблицы равны соответственно элементам разрешающей строки старой таблицы, деленным на разрешающий элемент.

3)оставшиеся элементы разрешающего столбца из выражений (2) и(3) новой таблицы равны соотв. элементам разрешающего столбца старой таблицы, деленным на разрешающий элемент и изменением знака на противоположный.

4)из формул (2) и (3) следует, что все оставшиеся элементы рассчитываются по правилу прямоугольника. Для этого, чтобы получить элемент новой таблицы, надо из соотв. элемента новой таблицы вычесть произведение второстепенной диагонали разделенное на разрешающий элемент.

18) Теорема Если в индексной строке последней симплексной табл, содержащей оптимальный план, имеется хотя бы одна нулевая оценка, соответствующая свободной переменной, то ЗЛП имеет бесконечное множество оптимальных планов

Доказательство. Пусть в оптимальном плане Aj₀ = О, где jo принадлежит множеству индексов СП, а минимальное симплексное отношение соответствует строке iго- Тогда, введя Xj₀ в базис, получим новое значение ЦФ.

Значение ЦФ при переходе к новому опор­ному плану не изменилось.

Если нулевых небазисных оценок в последней симплексной таблице окажется несколько, то, введя каждую из соответ­ствующих переменных в базис, найдем оптимальные планы x1*,x2*,... ,хk*, для которых значение ЦФ будет одно и то же, т. е.

Z(x1)=z(x2)=…z(xk)

Согласно второй части основной теоремы линейного про­граммирования, в этом случае оптимальным будет любой план, являющийся их выпуклой линейной комбинацией, т.е. общее решение примет вид

λ =λ1x1+λ2x2+…..+λkxk, λ1+λ2+….+λk=1

λi≥0 (i=1,k)

Эта ф-ла опред-т бесконечное мн-во оптимальн. Планов.

Следств: Если в инд. Строке симпл. табл, содержащей оптимальный план, все оценки СП положит., то найденные опт план и единств.

19) Теорема 1.10. Если в индексной строке симплексной та­блицы ЗЛП на максимум содержится отрицательная оцен­ка ∆j₀ < 0, а в соответствующем столбце переменной Xj₀ нет ни одного положительного элемента, то целевая функ­ция на множестве допустимых планов задачи не ограничена сверху.

Доказательство. Если бы все оценки индексной стро­ки Aj были неотрицательны, то опорный план был бы опти­мальным. Пусть ∆j₀ < 0. Тогда можно попытаться, не изме­няя нулевых значений всех свободных переменных x_m+i,... , х_п в равенстве (1.95), кроме Xj₀, увеличить значение целевой функции Z за счет увеличения переменной Xj₀ > 0. Полагая в равенствах (1.96) все Xj, кроме Xj₀, равными нулю, получаем

Так как Xi≥ 0, то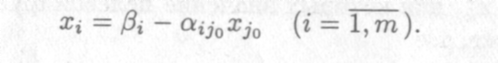

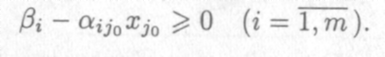
Пусть все aij₀ ≤ 0. Тогда при любом Xi₀ ≥ 0 имеем Xi ≥ 0. Что касается целевой функции Z, то, взя^тз в качестве Xj₀ достаточно большое положительное число, вследствие того, что ∆j₀ < 0, можно сделать значение

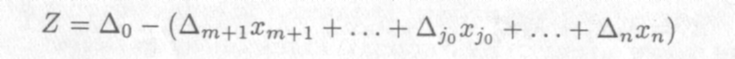
как угодно большим. В самом деле, так как ∆j₀ < 0, при Xj₀ —> оо имеем Z = ∆о — ∆j₀Xj₀ —► оо, т.е. целевая функция Z не ограничена сверху.

рямая и двойственная задача

Рассмотрим задачу вида:

Max F=c₁x ₁+c₂x₂+…+c_nx_n

a₁₁x₁+a₁₂x₂+…+a_1nx_n≤b₁

......................................

a_k1x₁+a_k2x₂+…+a_knx_n≤b_k

a_k+1,1x₁+a_k+1,2x₂+…+a_k+1,nx_n=b_k+1

…………………………………………..

a_m1x₁+a_m2x₂+…+a_mnx_n=b_m

x_j≥0, j=1,l; x_j-произвольные, j=l+1,n

Двойственной по отношению к исходной(прямой) задаче наз. задача вида:

min α=b₁y₁+b₂y₂+…+b_my_m

a₁₁y₁+a₂₁y₂+…+a_m1y_m≥c₁

…………………………………..

a_1ly₁+a_2ly₂+…+a_mly_m≥c_l

a_1,l+1y₁+a_2,l+1y₂+…+a_m,l+1y_m=c_l+1

…………………………………………….

a_1ny₁+a_2ny₂+…+a_mny_m=c_n

y_i≥0, i=1,k; y_i-произвольные, i=k+1,m

Сравнивая 2 задачи видно, что:

1)если у прямой задачи ЦФ на max ,то в дв-ной на min и наоборот.

2)коэф-ми при неизвестных ЦФ дв-ной задачи явл-ся свободные члены прямой задачи, а правыми частями в осн-х ограничениях дв-ной задачи явл-ся коэф-ты при неизвестных ЦФ прямой задачи.

3)матрица, составленная из коэф-тов осн-х ограничений прямой задачи и аналогичная матрица дв-ной задачи получаются друг из друга транспонированной.

4)число переменных прямой задачи равно числу ограничений дв-ной задачи и наоборот.

5)если переменная x_j прямой задачи принимает только неотрицательные значения, то j-ое ограничение в системе осн-х ограничений дв-ной задачи явл-ся неравенством. Если же x_j прямой задачи может принимать любые значения, то j-ое ограничение в системе осн-х ограничений дв-ной задачи явл-ся уравнением.