Теория массового обслуживания

Теория массового обслуживания изучает класс случайных процессов, среди которых находятся те, к которым все привыкли в бытовой жизни, когда имеем дело с ремонтными мастерскими, билетными кассами, справочными бюро и т.д. Всякая система массового обслуживания (СМО) предназначена для обслуживания некоторого потока заявок, поступающих, вообще говоря, в случайные моменты времени. СМО состоит из некоторого числа обслуживающих единиц, которые в теории массового обслуживания принято именовать приборами, или «каналами обслуживания». Обслуживание заявки также длится случайное время. Процесс работы СМО является случайным с дискретными состояниями и непрерывным временем.

Предмет теории массового обслуживания — построение математических моделей, связывающих заданные условия работы СМО (число каналов, их производительность, правила работы, характер заявок) с интересующими нас характеристиками — показателями эффективности СМО, описывающими ее способность справляться с потоком заявок. Такими показателями могут быть, например, среднее число заявок, обслуживаемых СМО в единицу времени, среднее число заявок в очереди, среднее время обслуживания одной заявки и т. д.

Математический анализ работы СМО очень облегчается, если все потоки, как входящие в СМО, так и внутренние — от одного прибора к другому, являются стационарными и пуассоновскими. В этом случае функционирование СМО описывается уравнениями Колмогорова и, как правило, можно получить аналитические формулы, дающие характеристики СМО в зависимости от условий работы СМО. Если в системе имеются непуассоновские потоки, то получить явные аналитические формулы для интересующих нас характеристик не удается, и для их определения необходимо прибегать к имитации.

СМО делятся на типы в зависимости от признаков — СМО с отказами и с очередью. В СМО с отказами заявка, поступившая в момент, когда все каналы заняты, покидает СМО; в СМО с очередью — становится в очередь. СМО с очередью подразделяются в зависимости от того, как организована очередь — ограничена она или нет. Кроме того, СМО делятся на два класса: открытые и замкнутые. В открытой СМО характеристики потока заявок не зависят от того, в каком состоянии находится сама СМО, в замкнутой — зависят. Имеются и другие признаки, по которым классифицируются СМО.

Одна из простейших СМО — n-канальная с отказами: пуассо-новский поток интенсивности поступает на систему обслуживания, состоящую из n одинаковых параллельных приборов (каналов обслуживания). Каждый прибор также является «пуассо-новским»: если заявка находится на обслуживании, то вероятность, что ее обслуживание закончится на малом интервале dt, дается формулой

P(dt) = dt + o(dt). (4.11)

(«Пуассоновский» прибор продуцирует пуассоновский поток обслуженных им заявок.)

Данная СМО может находиться в n состояниях. Состояние s_i — это ситуация, когда i приборов заняты обслуживанием заявок, а остальные свободны. Финальные вероятности p_i( 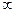) в этой системе даются формулами

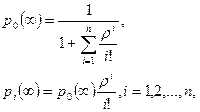(4.12)

где 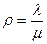. Эти формулы называются формулами Эрланга. Располагая финальными вероятностями (4.11), (4.12), можно вычислить все интересующие нас характеристики данной СМО.

Например, вероятность Р_отк того, что пришедшая заявка не будет обслужена (т. е. в момент ее прихода все п приборов будут заняты), дается формулой

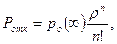
среднее число l занятых приборов — формулой

и т.д. Аналогично рассчитываются другие типы СМО, если все потоки в них являются пуассоновскими.

Если хотя бы один поток в СМО не является пуассоновским, то получение аналитических формул, связывающих показатели эффективности СМО и ее характеристики, становится крайне затруднительным. Естественным методом расчета таких СМО становится имитация — воспроизведение на ЭВМ реализаций случайного процесса функционирования СМО с последующей обработкой результатов методами математической статистики.

В первых главах было введено понятие «сложный процесс»: таковым считается процесс, прогноз которого недоступен технологии математического моделирования при данном уровне ее развития. Будем считать, что это — внешняя характеристика сложного процесса. Здесь дадим другую характеристику этого понятия, которую по сравнению с той, которая была дана в гл. 1, можно охарактеризовать как внутреннюю. Именно среди «сложных» процессов значительный класс составляют процессы, которые являются совокупностью нескольких одновременно протекающих взаимосвязанных, но разномасштабных по времени процессов, для составления моделей которых необходимы отличающиеся на порядки характерные масштабы осреднения величин по времени. Достаточно часто встречается ситуация, когда среди взаимодействующих процессов можно выделить небольшое количество «главных», характеристики которых нас интересуют и именно ради прогноза этих характеристик разрабатывается модель. Характерный временной масштаб остальных процессов много меньше и их характеристики нас интересуют постольку, поскольку они влияют на характеристики главных процессов. Таким образом, происходящие процессы делятся на медленные, прогноз развития которых нас интересует, и быстрые, характеристики которых нас не интересуют, однако влияние их на медленные нужно уметь учитывать.

В таких случаях характерный временной масштаб осреднения выбирается так, чтобы иметь возможность составить модель развития главных процессов с учетом их взаимодействия. Что касается быстрых процессов, то в рамках создаваемой модели, характерный временной масштаб которой определяется главными процессами, разрабатывают алгоритмы, рассчитывающие моменты осуществления быстрых процессов и их результат, т. е. изменения, которые осуществление этих процессов вносит в интересующие нас внешние величины главных процессов. Возможны два подхода к моделированию влияния быстрых процессов на медленные. Первый состоит в разработке модели их развития с соответствующим характерным временным масштабом осреднения, много меньшим, чем у главных процессов. При этом в модели появляется также и два времени — медленное и быстрое. При расчете развития быстрого процесса в соответствии с его моделью характеристики медленных процессов не меняются, т. е. медленное время как бы стоит на месте. Результатом расчета быстрого процесса является изменение характеристик медленных процессов с точки зрения медленного времени, происходящего мгновенно.

Для того чтобы иметь возможность реализовать способ расчета влияния быстрых процессов на медленные, необходимо вводить соответствующие внешние величины, идентифицировать и верифицировать эти модели, что усложняет все этапы технологии математического моделирования. Второй путь моделирования влияния быстрых процессов на медленные состоит в отказе от описания их развития с помощью моделей и рассмотрения их характеристик как случайных величин. Для реализации этого способа необходимо иметь функции распределения тех случайных величин, которые характеризуют влияние быстрых процессов на медленные, а также зависимость этих функций распределения от характеристик медленных процессов. В модели должны по-прежнему присутствовать алгоритмы, определяющие моменты наступления быстрых процессов. В эти моменты все внутренние величины медленных процессов должны быть известны. Вместо расчета развития быстрых процессов производится выброс случайного числа и в зависимости от выпавшего значения в соответствии с известными функциями распределения случайных величин, характеризующих результат протекания быстрых процессов, определяется, какое значение примут эти величины, и таким образом рассчитывается влияние быстрых процессов на медленные. В результате характеристики медленных процессов также станут случайными величинами. Какой из этих способов учета влияния быстрых процессов на медленные предпочтительней, зависит от целей моделирования, необходимой точности прогноза, имеющихся инструментов и т. д. Необходимо заметить, что при первом способе моделирования влияния быстрых процессов на медленные, когда составляется модель некоторого быстрого процесса, то мы часто находимся в той же позиции, в какой находились при составлении модели исходного процесса. Именно моделируемый быстрый процесс становится медленным, главным, на его течение влияют быстрые уже по отношению к нему процессы и это влияние опять можно моделировать двумя способами. Эта иерархическая вложенность быстрых процессов в медленные — одна из составляющих того качества моделируемого процесса, который назовем внутренней сложностью. Одна из причин почти неизбежного появления случайных факторов в модели сложного в таком понимании процесса — необходимость на каком-то уровне описанной иерархии отказываться от первого способа моделирования влияния очередного быстрого процесса на медленные при составлении их математической модели.

Деление изучаемых взаимодействующих процессов на быстрые и медленные при составлении их математической модели — типичный пример ситуации, когда в модели появляются случайные факторы, о которых шла речь при объяснении терминов «имитационная модель», «имитационное моделирование». В этом случае, как уже отмечалось, интересующие нас характеристики медленных процессов становятся случайными величинами, и для вычисления их статистических характеристик необходимо выполнять имитацию в том смысле, в котором этот термин понимается в теории вероятностей и математической статистике, т.е., выполняя серию имитационных экспериментов, получать реализации интересующих нас случайных величин и производить затем обработку результатов методами математической статистики.

Приведем пример имитационного моделирования такого случайного процесса. Пусть имеется некоторая компания Orient, выпускающая однотипную продукцию (на картинках эта продукция похожа на банки с вареньем). Время выпуска единицы продукции случайно и распределено равномерно около величины l на отрезке [l — d, l+ d]. После изготовления продукция попадает на склад. Фирма имеет магазин, где реализует выпущенную продукцию. Магазин удален от склада. В магазин за продукцией приходят клиенты. Поток клиентов в магазин — пуассоновский с пуассоновской постоянной . Пришедший клиент с вероятностью 0,1 пришел за четырьмя единицами продукта, с вероятностью 0,4 — за пятью, с вероятностью 0,3 — за шестью и, наконец, с вероятностью 0,2 — за семью единицами продукта. Запаса продукта в магазине нет, он заказывается со склада каждый раз в соответствии с требованием клиента. На перевозку продуктов со склада в магазин требуется время R, кроме того, перед выдачей заказ упаковывается, на что требуется время P.

Рис. 4.1. Перевозка продуктов со склада в магазин, упаковка не загружена, в очереди один клиент (с запросом четырех единиц товара), еще три клиента подходят, девушка с запросом на шесть единиц и двое мужчин с запросами по пять единиц. Одна девушка уже получила свои шесть единиц и увозит их на тележке. На рис 4.1 и 4.2 на складе всего одна единица товара и еще одна движется на склад по конвейеру

Рис. 4.2. Момент, когда перевозка простаивает, а упаковка работает. В очереди два клиента, мужчина с запросом пяти единиц и девушка с запросом шести единиц товара. Трое клиентов уходят ни с чем, еще трое подходят к магазину. В окне статистики выводится модельное время, сколько клиентов прибыло, сколько ушли ни с чем, процент загрузки упаковки, среднее количество заявок на товар в очереди и, наконец, среднее время ожидания клиента

Клиент стоит в очереди, пока обслуживаются другие клиенты и пока его заказ перевозится со склада и упаковывается. Считается, что если клиент подходит к магазину, а там уже есть очередь с общим заказом более 10 единиц продукта, то клиент не становится в очередь, а уходит ни с чем. Величины , l, R и Р считаются управлениями, т. е. в любой момент их можно менять в некоторых пределах.

Данная модель была реализована, средствами инструментальной системы имитационного моделирования MISS, которая будет рассмотрена в следующей главе. На рис. 4.1 и 4.2 внизу показаны два момента работы модели.

Можно было бы также вычислять и какие-то другие, важные для данной модели величины, например средний запас продукта на складе.

Несмотря на всю простоту данной модели, было бы весьма затруднительно аналитически вычислить такие, например, величины, как загрузка упаковки, среднее количество заявок в очереди, процент необслуженных клиентов, а тем более их зависимость от управлений. Проведение же серии имитационных экспериментов позволяет набрать достаточно представительное множество реализаций этих величин и искать интересующие зависимости статистическими методами.

В настоящее время одним из наиболее эффективных, если не единственным, инструментом анализа динамических случайных процессов является инструмент имитационного моделирования. Для его эффективного использования необходимо при создании имитационной модели того или иного явления тщательно проанализировать структуру модели с привлечением теоретических результатов, описанных в гл. 1.

Литература. Ю.Н. Павловский, Н.В. Белотелов, Ю.И. Бродский Имитационное моделирование. М.: Изд. Центр «Академия», 2008г.