Формирование умозаключений
Def10. Умозаключение – это форма мышления, в которой из одного или нескольких суждений на основании определенных правил вывода получаются новые суждения.
В обучении математике они принимают вид целей и специальных методов обучения. Основные виды умозаключений:
· индукция (полная, неполная) – вид умозаключения, при котором из одного или нескольких частных суждений получается _________ суждение (метод – индуктивного обобщения), результат неполной индукции правдоподобные суждения, полной индукции – достоверные.
· дедукция – вид умозаключения, при котором по правилам логического вывода осуществляется переход от одного или нескольких суждений - посылок к суждению – ____________, результат - достоверное суждение.
· аналогия (строгая, не строгая) - вид умозаключения, при котором на основании существования некоторых сходных свойств у объектов получают суждение о ___________________. Строгая аналогия основана на существовании между объектами отношения _____________. Метод аналогий используется в обучении математике как метод подведения учащихся к ______________.
· Задание 7. Получите суждение, являющиеся результатом указанного умозаключения, и выясните, является ли оно справедливым:
| Исходное (ые) суждение(я) | Вид умозаключения | Суждение-результат |
1. При n = 1 и при n = 2 значение функции 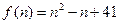 - простое число - простое число | Неполная индукция | |
2. Площадь тупоугольного и остроугольного треугольников равна 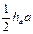 ; площадь прямоугольного треугольника равна ; площадь прямоугольного треугольника равна 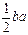 | Полная индукция | |
| 3. Диагонали прямоугольника равны. АВСD – прямоугольник | Дедукция | |
4. Площадь треугольника равна 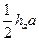 | Нестрогая аналогия | |
| 5. Скалярное произведение векторов равно сумме произведений их соответствующих координат | Строгая аналогия |
Задание для самостоятельной работы: пользуясь материалами курса «Введение в математику» вспомните определение понятия «логическое следование», основные виды логических правил вывода.
Важной задачей обучения математике является формирование умений осуществлять дедуктивные умозаключения и умений проводить доказательства на уровне строгости, соответствующем содержательному доказательству.
Задание для самостоятельной работы: пользуясь материалами курса «Введение в математику» вспомните, что называется доказательством, чем отличаются содержательные и формальные доказательства, какие существуют методы доказательства математических утверждений (прямое доказательство, косвенный метод доказательства и его разновидности, метод полной математической индукции).
Обучение дедуктивным умозаключениям и доказательству осуществляется в процессе ____________________ доказательства математических суждений с последующей организацией работы по __________, в процессе постановки задач на __________
______, а также через систематическое предъявление к учащимся требований _______
__________________ положениями математической теории, а также посредством запрета на получение суждений посредством ____________________________________.
Технологическая цепочка (методическая схема) работа с доказательством теоремы:
| Название этапа | Содержание этапа | Результат |
| 1. Подготовительный этап | Мотивация необходимости установления истинности утверждений посредством его доказательства, подготовка учащихся к восприятию доказательства или к его открытию. | Формирование потребности в доказательстве. Готовность учащихся к пониманию доказательства. |
| 2. Основной этап | Демонстрация учащимся доказательства утверждения или включение их в деятельность самостоятельного проведения доказательства. Включение учащихся в деятельность осмысления хода доказательства. | Формирование готовности к воспроизведению хода доказательства утверждения, к его описанию и анализу. |
| 3. Этап закрепление. | Включение учащихся в деятельность переноса способа доказательства утверждения в сходные ситуации. | Формирование готовности к применению идеи, метода доказательства, отдельных приемов доказательства. |
