Задания для индивидуальной работы
Задание 1. Дан параллелограмм ABCD, три вершины которого заданы. Найти: 1) четвертую вершину; 2) острый угол параллелограмма.
1. A(-1; -2; 3), B(-4; 1; 2), C (5; 2; 7).
2. A(1; 2; 3), B(3; -4; -2), C (-4; -3; 2).
Задание 2. Даны векторы  ,
, 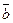 ,
, 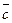 и
и 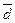 . Показать, что векторы
. Показать, что векторы 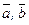 и
и 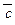 можно взять в качестве базиса. Найти координаты вектора
можно взять в качестве базиса. Найти координаты вектора 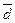 относительно выбранного базиса.
относительно выбранного базиса.
1. 
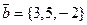 ,
, 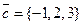 ,
, 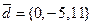 .
.
2. 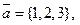
 ,
, 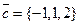 ,
, 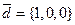 .
.
Задание 3. Найти собственные значения и собственные векторы линейного оператора, заданного матрицей
1. 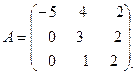 2.
2.  3.
3. 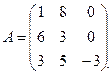
Задание 4. Привести к каноническому виду квадратичную форму
1.  .
.
2.  .
.
3. 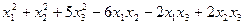 .
.
Задание 5. Исследовать на знакоопределенность квадратичную форму
1. 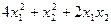 .
.
2.  .
.
3.  .
.
4. СЛОВАРЬ ТЕРМИНОВ (ГЛОССАРИЙ)
Матрицейразмера 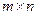 , где
, где  - число строк,
- число строк,  - число столбцов, называется прямоугольная таблица чисел, расположенных в определенном порядке. Эти числа называются элементами матрицы. Место каждого элемента однозначно определяется номером строки и столбца, на пересечении которых он находится. Элементы матрицы обозначаются
- число столбцов, называется прямоугольная таблица чисел, расположенных в определенном порядке. Эти числа называются элементами матрицы. Место каждого элемента однозначно определяется номером строки и столбца, на пересечении которых он находится. Элементы матрицы обозначаются 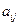 , где
, где  - номер строки, а
- номер строки, а  - номер столбца
- номер столбца 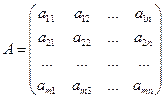
Если число столбцов матрицы равно числу строк  , то матрица называется квадратной.Если
, то матрица называется квадратной.Если 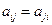 , то матрица называется симметрической.
, то матрица называется симметрической.
Квадратная матрица вида 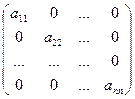 называется диагональнойматрицей.
называется диагональнойматрицей.
Квадратная матрица вида 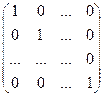 называется единичной матрицей. Единичная матрица обозначается символом
называется единичной матрицей. Единичная матрица обозначается символом 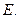
Матрица, все элементы которой равны  , называется нулевойматрицей. Нулевая матрица обозначается символом
, называется нулевойматрицей. Нулевая матрица обозначается символом 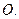
Суммой (разностью) матриц 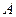 и
и  называется матрица
называется матрица 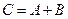 ,
, 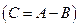 элементами которой являются соответственно сумма (разность) элементов исходных матриц
элементами которой являются соответственно сумма (разность) элементов исходных матриц
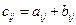
 .
.
Операция умножения (деления) матрицы любого размера на произвольное число сводится к умножению (делению) каждого элемента матрицы на это число

Произведениемматрицы 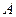 на матрицу
на матрицу  называется матрица
называется матрица 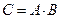 , элементы которой могут быть вычислены по формуле
, элементы которой могут быть вычислены по формуле
 .
.
Из приведенного определения видно, что операция умножения матриц определена только для матриц, число столбцов первой из которых равно числу строк второй.Умножение матриц, вообще говоря, не коммутативно, т.е.  даже если определены оба произведения. Однако, если для каких - либо матриц равенство
даже если определены оба произведения. Однако, если для каких - либо матриц равенство 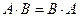 выполняется, то такие матрицы называются перестановочными.
выполняется, то такие матрицы называются перестановочными.
Матрицу  называют транспонированнойматрицей А, а переход от А к В транспонированием, если элементы каждой строки матрицы А записать в том же порядке в столбцы матрицы В другими словами, если
называют транспонированнойматрицей А, а переход от А к В транспонированием, если элементы каждой строки матрицы А записать в том же порядке в столбцы матрицы В другими словами, если 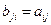 . Матрица, транспонированная матрице
. Матрица, транспонированная матрице 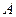 обозначается символом
обозначается символом 
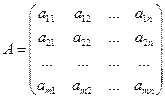
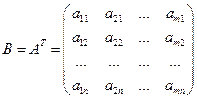
Определителем (детерминантом)квадратной матрицы 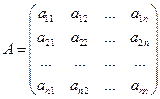 называется число, которое может быть вычислено по элементам матрицы по формуле
называется число, которое может быть вычислено по элементам матрицы по формуле 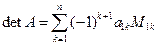 , где
, где  – детерминант матрицы, полученной из исходной вычеркиванием первой строки и
– детерминант матрицы, полученной из исходной вычеркиванием первой строки и  – го столбца. Определитель может вычисляться по любой строке или столбцу матрицы, т.е. справедлива формула
– го столбца. Определитель может вычисляться по любой строке или столбцу матрицы, т.е. справедлива формула
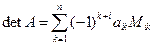 ,
, 
Определитель единичной матрицы равен 1. Для указанной матрицы А число  называется дополнительным минором элемента матрицы
называется дополнительным минором элемента матрицы 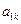 . Таким образом, можно заключить, что каждый элемент матрицы имеет свой дополнительный минор. Дополнительные миноры существуют только в квадратных матрицах.
. Таким образом, можно заключить, что каждый элемент матрицы имеет свой дополнительный минор. Дополнительные миноры существуют только в квадратных матрицах.
Если в матрице А выделить несколько произвольных строк и столько же произвольных столбцов, то определитель, составленный из элементов, расположенных на пересечении этих строк и столбцов называется миноромматрицы А. Если выделено 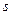 строк и столбцов, то полученный минор называется минором порядка s.
строк и столбцов, то полученный минор называется минором порядка s.
Если вычеркнуть из исходной квадратной матрицы А выделенные строки и столбцы, то определитель полученной матрицы называется дополнительным минором.
Алгебраическим дополнением минора матрицы называется его дополнительный минор, умноженный на 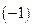 в степени, равной сумме номеров строк и номеров столбцов минора матрицы. В частном случае, алгебраическим дополнением элемента матрицы называется его минор, взятый со своим знаком, если сумма номеров столбца и строки, на которых стоит элемент, есть число четное и с противоположным знаком, если нечетное.
в степени, равной сумме номеров строк и номеров столбцов минора матрицы. В частном случае, алгебраическим дополнением элемента матрицы называется его минор, взятый со своим знаком, если сумма номеров столбца и строки, на которых стоит элемент, есть число четное и с противоположным знаком, если нечетное.
Столбцы (строки) матрицы называются линейно зависимыми, если существует их линейная комбинация, равная нулю, имеющая нетривиальные (не равные нулю) решения.
Элементарными преобразованиями матрицы называются следующие преобразования:
1) умножение строки на число, отличное от нуля;
2) прибавление к одной строке другой строки;
3) перестановка строк;
4) вычеркивание (удаление) одной из одинаковых строк (столбцов);
5) транспонирование.
Те же операции, применяемые для столбцов, также называются элементарными преобразованиями. С помощью элементарных преобразований можно к какой-либо строке или столбцу прибавить линейную комбинацию остальных строк (столбцов).
Если существуют квадратные матрицы Х и А одинакового порядка, удовлетворяющие условию  где
где 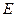 - единичная матрица того же порядка, то матрица
- единичная матрица того же порядка, то матрица  называется обратной по отношению к матрице А и обозначается
называется обратной по отношению к матрице А и обозначается 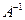
Базисным минором матрицы порядка 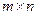 называется минор порядка
называется минор порядка  , если он не равен нулю, а все миноры порядка
, если он не равен нулю, а все миноры порядка 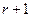 и выше равны нулю, или не существуют вовсе, т.е. число
и выше равны нулю, или не существуют вовсе, т.е. число  совпадает с меньшим из чисел
совпадает с меньшим из чисел  или
или  .
.
Столбцы и строки матрицы, на которых стоит базисный минор, называются базисными. В матрице может быть несколько различных базисных миноров, имеющих одинаковый порядок.
Порядок базисного минора матрицы называется рангомматрицы. Элементарные преобразования не изменяют ранг матрицы.
Матрицы, полученные в результате элементарного преобразования, называются эквивалентными.
Системой m линейных алгебраических уравнений относительно n неизвестных  называется система
называется система
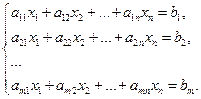
Решениемсистемыm линейных алгебраических уравнений относительно n неизвестных  называется совокупность n значений неизвестных
называется совокупность n значений неизвестных 
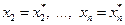 , при подстановке которых все уравнения системы обращаются в тождества.
, при подстановке которых все уравнения системы обращаются в тождества.
Система, имеющая хотя бы одно решение, называется совместной; система, не имеющая ни одного решения - несовместной.
Если правая часть системы m линейных алгебраических уравнений относительно n неизвестных  равна нулю, то система называется однородной.
равна нулю, то система называется однородной.
Система из 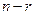 линейно независимых решений линейной однородной системы называется фундаментальной системой решений.Фундаментальная система решений образует базис в подпространстве решений линейной однородной системы.
линейно независимых решений линейной однородной системы называется фундаментальной системой решений.Фундаментальная система решений образует базис в подпространстве решений линейной однородной системы.
Общим решением линейной системыназывается выражение, позволяющее вычислить все решения системы.
Комплексным числом  называется упорядоченная пара действительных чисел
называется упорядоченная пара действительных чисел  и
и 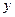 :
:  , где
, где 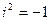 (число
(число  называется мнимой единицей).
называется мнимой единицей).
Комплексные числа 
 называются сопряженными друг другу.
называются сопряженными друг другу.
Пусть 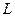 - множество элементов, для которых определены операции сложения и умножения на число, причём эти операции обладают следующими свойствами. Для любых элементов
- множество элементов, для которых определены операции сложения и умножения на число, причём эти операции обладают следующими свойствами. Для любых элементов 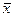 ,
,  ,
,  из множества
из множества 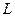 выполняются законы
выполняются законы
1) 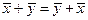 (коммутативность сложения);
(коммутативность сложения);
2)  (ассоциативность сложения);
(ассоциативность сложения);
3) во множестве 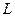 существует нулевой элемент
существует нулевой элемент  такой, что для любого элемента
такой, что для любого элемента  ,
, 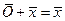 (существование нулевого элемента);
(существование нулевого элемента);
4) для любого элемента  существует элемент
существует элемент 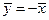 , такой, что
, такой, что  (существование противоположного элемента);
(существование противоположного элемента);
5) 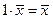 .
.
Для любых действительных чисел 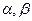 любых элементов
любых элементов 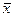 ,
,  из множества
из множества 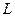 ;
;
6) 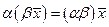 ;
;
7) Распределительный закон  ;
;
8)  .
.
Множество 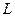 называется линейным (векторным) пространством, а его элементы называются векторами.
называется линейным (векторным) пространством, а его элементы называются векторами.
Если операции сложения и умножения на число определены для действительных элементов, то линейное (векторное) пространство является вещественным пространством, если для комплексных элементов – комплексным пространством.
Говорят, что в линейном пространстве 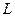 задано некоторое линейное преобразование А, если любому элементу
задано некоторое линейное преобразование А, если любому элементу  по некоторому правилу ставится в соответствие элемент
по некоторому правилу ставится в соответствие элемент 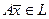 .
.
Преобразование А называется линейным, если для любых векторов  и
и 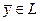 и любого
и любого  выполняются равенства
выполняются равенства 

Линейное преобразование называется тождественным, если оно преобразует каждый элемент линейного пространства в себя  .
.
Если в пространстве 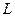 существуют векторы линейного преобразования
существуют векторы линейного преобразования 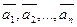 , то другой вектор
, то другой вектор 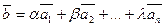 является линейной комбинацией векторов
является линейной комбинацией векторов 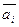 .
.
Если  выполняется только при
выполняется только при  , то векторы
, то векторы 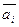 называются линейно независимыми.
называются линейно независимыми.
Если в линейном пространстве 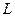 есть n линейно независимых векторов, а любые
есть n линейно независимых векторов, а любые  векторов линейно зависимы, то пространство
векторов линейно зависимы, то пространство 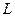 называется n-мерным, а совокупность линейно независимых векторов называется базисом линейного пространства
называется n-мерным, а совокупность линейно независимых векторов называется базисом линейного пространства 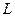 .
.
Если вектор 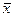 переводится в вектор
переводится в вектор  линейным преобразованием с матрицей А, а вектор
линейным преобразованием с матрицей А, а вектор  в вектор
в вектор 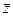 линейным преобразованием с матрицей В, то последовательное применение этих преобразований равносильно линейному преобразованию, переводящему вектор
линейным преобразованием с матрицей В, то последовательное применение этих преобразований равносильно линейному преобразованию, переводящему вектор 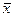 в вектор
в вектор 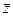 (оно называется произведением составляющих преобразований).
(оно называется произведением составляющих преобразований).
Пусть 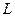 – заданное n- мерное векторное пространство. Ненулевой вектор
– заданное n- мерное векторное пространство. Ненулевой вектор  называется собственным вектором линейного преобразования А, если существует такое число l, что выполняется равенство:
называется собственным вектором линейного преобразования А, если существует такое число l, что выполняется равенство:  . При этом число
. При этом число 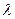 называется собственным значением (характеристическим числом)линейного преобразования А, соответствующего вектору
называется собственным значением (характеристическим числом)линейного преобразования А, соответствующего вектору 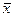 .
.
Если линейное преобразование А в некотором базисе 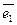 ,
,  ,…,
,…, 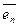 имеет матрицу
имеет матрицу 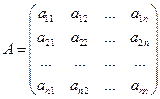 , то собственные значения линейного преобразования А можно найти как корни
, то собственные значения линейного преобразования А можно найти как корни 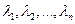 уравнения:
уравнения: 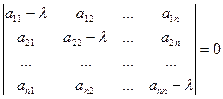 .
.
Это уравнение называется характеристическим уравнением, а его левая часть - характеристическим многочленом линейного преобразования А. Характеристический многочлен линейного преобразования не зависит от выбора базиса.
Однородный многочлен второй степени относительно переменных 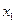 и
и 
 не содержащий свободного члена и неизвестных в первой степени называется квадратичной формой переменных
не содержащий свободного члена и неизвестных в первой степени называется квадратичной формой переменных 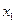 и
и  .
.
Однородный многочлен второй степени относительно переменных 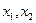 и
и 
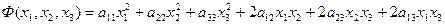 ,
,
не содержащий свободного члена и неизвестных в первой степени называется квадратичной формой переменных 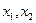 и
и  .
.
Квадратичная форма от n неизвестных называется положительно определенной, если ее ранг равен положительному индексу инерции и равен числу неизвестных.
Вектором(на прямой, на плоскости, в пространстве) называется упорядоченная пара точек А, В, или направленный отрезок. Точка А называется началом вектора, точка В - его концом. Вектор, начало и конец которого совпадают, называется нуль-вектором. Векторы обычно обозначаются или двумя большими буквами со стрелкой или чертой наверху, или малой буквой также со стрелкой или чертой наверху: 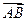 ,
,  ,
,  ,
, 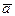 . Первая из двух букв означает начало вектора, вторая - его конец.
. Первая из двух букв означает начало вектора, вторая - его конец.
Длина отрезка 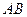 называется длиной или модулем вектора и обозначается
называется длиной или модулем вектора и обозначается  или
или  .
.
Два ненулевых вектора 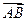 и
и 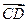 называются коллинеарными, если они лежат на одной или на параллельных прямых. Обозначение:
называются коллинеарными, если они лежат на одной или на параллельных прямых. Обозначение: 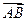 ïê
ïê 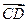 .
.
Коллинеарные векторы называются одинаково (противоположно) направленными, если (в случае принадлежности разным прямым) их концы лежат по одну сторону (по разные стороны) от прямой, соединяющей их начала, а в случае принадлежности одной прямой, если из двух лучей, определяемых этими векторами, один содержится (не содержится) в другом. Обозначение 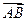
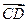 (
( 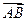 ¯
¯ 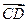 ).
).
Два вектора 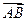 и
и 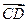 называются равными, если они одинаково направлены и имеют равные длины, т.е. если
называются равными, если они одинаково направлены и имеют равные длины, т.е. если 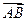
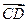 , ï
, ï 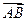 ï=ï
ï=ï 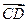 ï.
ï.
Отложить вектор  от точкиМ -значит построить вектор
от точкиМ -значит построить вектор 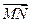 , равный вектору
, равный вектору  .
.
Суммой  векторов
векторов 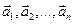 называется вектор
называется вектор 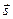 , получающийся следующим построением: от произвольной точки А (прямой, плоскости, пространства) откладываем первый вектор
, получающийся следующим построением: от произвольной точки А (прямой, плоскости, пространства) откладываем первый вектор 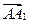 , равный вектору
, равный вектору  , от конца
, от конца 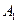 вектора
вектора 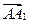 откладываем второй вектор
откладываем второй вектор 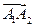 , равный вектору
, равный вектору  и т.д.: суммой
и т.д.: суммой 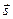 является вектор, соединяющий начальную точку А с концом
является вектор, соединяющий начальную точку А с концом 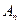 последнего отложенного вектора
последнего отложенного вектора 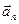 . Операция сложения векторов ассоциативна и коммутативна, так как при любом порядке откладывания векторов - слагаемых мы придем к тому же самому результату.
. Операция сложения векторов ассоциативна и коммутативна, так как при любом порядке откладывания векторов - слагаемых мы придем к тому же самому результату.
Произведением действительного ненулевого числа l на ненулевой вектор  называется вектор, обозначаемый
называется вектор, обозначаемый 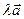 или
или 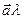 , удовлетворяющий следующим трем условиям:
, удовлетворяющий следующим трем условиям: 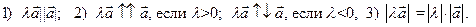
Произведение любого вектора на нуль и нуль-вектора на любое число, по определению, есть нуль-вектор, т.е. 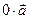 =
=  ,
,  =
=  .
.
Скалярным произведением двух ненулевых векторов  и
и 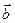 называется число, равное произведению длин этих векторов на косинус угла j между ними. Обозначение:
называется число, равное произведению длин этих векторов на косинус угла j между ними. Обозначение:  или
или  , т.е.
, т.е.  где
где 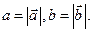 Если
Если  или
или  , то, по определению,
, то, по определению, 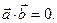
Декартова прямоугольная система координат в пространстве называется правой (левой), если поворот от базисного вектора  к вектору
к вектору  на наименьший угол виден с конца вектора
на наименьший угол виден с конца вектора 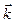 осуществляющимся против (по) часовой стрелки. Говорят также, что тройка базисных векторов
осуществляющимся против (по) часовой стрелки. Говорят также, что тройка базисных векторов  имеет правую (левую) ориентацию.
имеет правую (левую) ориентацию.
Векторным произведением двух неколлинеарных векторов  и
и 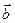 называется вектор
называется вектор 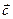 , перпендикулярный плоскости векторов
, перпендикулярный плоскости векторов  и
и 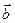 , имеющий длину, равную площади параллелограмма, построенного на векторах
, имеющий длину, равную площади параллелограмма, построенного на векторах  и
и 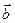 и направленный так, что тройка векторов
и направленный так, что тройка векторов 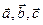 так же ориентирована, как и тройка базисных векторов
так же ориентирована, как и тройка базисных векторов  . Обозначение:
. Обозначение: 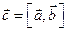 . Векторное произведение двух коллинеарных векторов и в случае, когда один или оба сомножителя - нуль-векторы, по определению, равно нулю.
. Векторное произведение двух коллинеарных векторов и в случае, когда один или оба сомножителя - нуль-векторы, по определению, равно нулю.
Смешанным произведением трех векторов 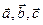 называется скалярное произведение векторного произведения первых двух векторов на третий. Обозначение:
называется скалярное произведение векторного произведения первых двух векторов на третий. Обозначение: 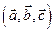 , т.е.
, т.е.  Из этого определения следует, что три вектора компланарны (параллельны одной плоскости) тогда и только тогда, когда их смешанное произведение равно нулю.
Из этого определения следует, что три вектора компланарны (параллельны одной плоскости) тогда и только тогда, когда их смешанное произведение равно нулю.
Любая прямая на плоскости может быть задана уравнением первого порядка 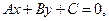
 Это уравнение называют общим уравнением прямой.
Это уравнение называют общим уравнением прямой.
Каждый ненулевой вектор  , компоненты которого удовлетворяют условию
, компоненты которого удовлетворяют условию  называется направляющим вектором прямой
называется направляющим вектором прямой  .
.
Направляющими косинусами прямой называются направляющие косинусы вектора 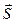 , которые могут быть вычислены по формулам:
, которые могут быть вычислены по формулам:
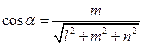 ;
; 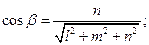
 .
.
Откуда 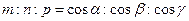 . Числа
. Числа 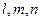 называются угловыми коэффициентами прямой.
называются угловыми коэффициентами прямой.
