Детектирование АМ сигналов

























 У АМ сигнала
У АМ сигнала 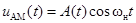 информация о модулирующем сигнале заключена в огибающей
информация о модулирующем сигнале заключена в огибающей  , следовательно необходим амплитудный детектор (детектор огибающей).По определению такой ФУ должен осуществлять измерение огибающей входного сигнала, т.е. формировать выходной сигнал вида uвых(t) = Кдет×А(t). Простейшая схема детектора огибающей на нелинейной основе приведена на рис. 3.24. В ней в качестве нелинейного элемента для обогащения спектра тока i низкочастотными составляющими модулирующего сигнала (напомним, что их нет в спектре входного АМ сигнала u1(t) ) используется диод. Для подавления высокочастотных спектральных составляющих (АМ сигнала и побочных продуктов нелинейного преобразования) служит простейший ФНЧ 1-го порядка – нагрузочная RC цепь. На рис. 3.25 приведены спектры входного u1(t) и выходного uн (t) напряжений, тока i диода и зависимость модуля сопротивления нагрузки от частоты zRC(w), вытекающие из приведённых рассуждений.
, следовательно необходим амплитудный детектор (детектор огибающей).По определению такой ФУ должен осуществлять измерение огибающей входного сигнала, т.е. формировать выходной сигнал вида uвых(t) = Кдет×А(t). Простейшая схема детектора огибающей на нелинейной основе приведена на рис. 3.24. В ней в качестве нелинейного элемента для обогащения спектра тока i низкочастотными составляющими модулирующего сигнала (напомним, что их нет в спектре входного АМ сигнала u1(t) ) используется диод. Для подавления высокочастотных спектральных составляющих (АМ сигнала и побочных продуктов нелинейного преобразования) служит простейший ФНЧ 1-го порядка – нагрузочная RC цепь. На рис. 3.25 приведены спектры входного u1(t) и выходного uн (t) напряжений, тока i диода и зависимость модуля сопротивления нагрузки от частоты zRC(w), вытекающие из приведённых рассуждений.
Проанализируем работу диодного детектора огибающей в режиме сильного сигнала. В этом случае целесообразно воспользоваться кусочно-линейной аппроксимацией вольтамперной характеристики (ВАХ) 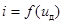 диода и расчёт вести методом угла отсечки. Можно наметить следующую последовательность рассуждений:
диода и расчёт вести методом угла отсечки. Можно наметить следующую последовательность рассуждений:
· для вычисления uн(t) при известной нагрузке (R и C) надо предварительно определить ток i,
· для вычисления тока i при выбранном диоде (известной ВАХ 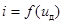 ) надо знать напряжение на нём uд,
) надо знать напряжение на нём uд,
· для определения напряжения  , надо знать искомое напряжение uн(t)
, надо знать искомое напряжение uн(t)
В результате образовался «замкнутый круг» – вычисление искомой функции требует знания её самой на стадии промежуточных вычислений. Для его «разрыва» воспользуемся методом итераций (последовательных приближений), суть которого в том, что задаются начальным («нулевым») приближением к искомой функции 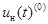 и производят вычисление её «первого» приближения
и производят вычисление её «первого» приближения 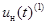 по выше намеченной процедуре (в обратном порядке):
по выше намеченной процедуре (в обратном порядке):
1) 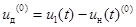 ,
,
2)  ,
,
3) 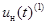 через
через  и известные R и C,
и известные R и C,
4) сравнивают разность  с допустимой погрешностью.
с допустимой погрешностью.
При циклическом повторении этой процедуры с ростом числа приближений возможны два варианта:
· процесс последовательных приближений сходится к истинному решению,
· процесс расходится.
В первом случае цикл прерывают по достижении заданной точности вычислений. Второй случай может свидетельствовать о «плохом» выборе «нулевого» приближения.
Для «удачного» выбора «нулевого» приближения и существенного сокращения числа итераций рекомендуется использование квазилинейного метода, в основе которого лежит допущение о форме искомого колебаний (вида функции), которым задаются с точность до его параметров.
Так, в нашем случае анализа диодного детектора, в качестве «нулевого» приближения к искомому напряжению на нагрузке примем постоянное напряжение 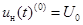 , не задавая его численно. Основания для этого чисто физические – напряжение на выходе ФНЧ не может быстро меняться во времени. Тогда, в соответствии с методом угла отсечки (см. рис. 3.26), имеем
, не задавая его численно. Основания для этого чисто физические – напряжение на выходе ФНЧ не может быстро меняться во времени. Тогда, в соответствии с методом угла отсечки (см. рис. 3.26), имеем
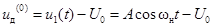 ;
;
 где
где  ;
;
 ,
,
где S – крутизна наклонного участка ВАХ диода;
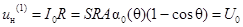 . (3.6)
. (3.6)
Уравнивая  , мы имеем возможность численно определить U0 и завершить процесс итераций.
, мы имеем возможность численно определить U0 и завершить процесс итераций.
Из (3.6) вытекает следующий результат
 , (3. 7)
, (3. 7)
на основе которого можно сделать следующие выводы:
1. Угол отсечки q и, соответственно, Кдет не зависят от огибающей А, следовательно, детектирование в режиме сильного сигнала осуществляется линейно.
2. Для повышения эффективности детектирования (увеличения Кдет) следует стремиться к уменьшению угла отсечки q, что достигается увеличением произведения S×R.
 3. Выражение (3.7) можно использовать в качестве
3. Выражение (3.7) можно использовать в качестве 













 формулы для расчёта сопротивления R нагрузки после выбора диода (становится известной крутизна S его ВАХ) и величины Кдет.
формулы для расчёта сопротивления R нагрузки после выбора диода (становится известной крутизна S его ВАХ) и величины Кдет.
4. Величину ёмкости С нагрузки следует определять из очевидного неравенства  .
.
Проведём анализ детектора огибающей в режиме слабого сигнала.
В этом случае ВАХ диода целесообразно аппроксимировать полиномом второй степени
 .
.
Ограничимся определением «первого» приближения 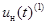 , приняв
, приняв 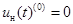 . Тогда
. Тогда  и
и

 .
.
В результате имеем (с учетом очевидного  )
)
 .
.
При простом АМ сигнале, когда 
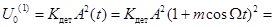
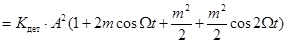 .
.
Из полученного результата видно, что детектирование сопровождается нелинейными искажениями с коэффициентом гармоник

и можно сделать следующие выводы:
1. В режиме слабого сигнала имеет место квадратичное детектирование, сопровождаемое нелинейными искажениями.
2. Величина нелинейных искажений, определяемая  , зависит от коэффициента модуляции m (
, зависит от коэффициента модуляции m (  ).
).
