Раздел «Элементы теории множеств»
1. Понятие множества
· Под множеством понимается некоторая вполне определенная совокупность объектов или элементов.
· Множество – совокупность некоторых(произвольных) объектов, объединённых по какому либо признаку.
· Множество – совокупность определенных различаемых объектов, причём таких, что для каждого объекта можно установить, принадлежит этот объект данному множеству или нет.
§ Множество – любая совокупность объектов, которая обладает следующими свойствами.
o Элементы множества представляют собой попарно различные объекты.
o Элементы и состав множества не меняется с течением времени.
o Объекты составляющие множество называются элементами множества и обозначающие маленькими латинскими буквами (например: x, a, b)
o Множества обычно обозначаются заглавными латинскими буквами ( Например: A, B, C, D)
Например: N - множество натуральных чисел. Z – множество целых чисел. И др.
{ 1,2,3,4} – множество содержит натуральные числа 1-2-3-4.
2. Понятие подмножества.
Множество А называют подмножеством множества В, если каждый элемент множества А является так же элементом множества В.
То что множество А является подмножеством множества В обозначается
так,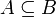 
: 
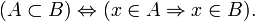
3. Понятие пустого множества
Пустое множество – это множество, не содержащие ни одного элемента. Оно обозначается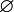 
и его мощность равна нулю (| 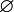|=0).
Пустое множество единственно.
Множество { 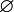} и { { 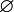} } не равномощные. В множестве { 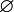} нет ни одного элемента, а в множестве { { 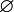} } есть один элемент пустое множество.
4. Понятие универсального множества.
Универсальное множество – есть множество, обладающие таким свойством, что все рассматриваемые множества являются его подмножествами.
В теории чисел универсальное множество обычно совпадает со множеством всех целых или натуральных чисел.
В математическом анализе универсальное множество может быть множеством всех действительных чисел.
5. Конечные\бесконечные множества, счетное множество, мощность множества, равномощное множество.
§ Множество называется конечным, если оно состоит из конечного числа элементов.
А = {а1,a2,….,a5}
§ Бесконечным является множество всех натуральных чисел, целых, действительных и тд.
§ Счётное множество – это множество А, все элементы которого могут быть занумерованы в бесконечную последовательность а1,а2,….,аn , так чтобы при этом каждый элемент получил лишь один номер n и каждое натуральное число n было бы номером лишь одного элемента множества А.
§ Мощностью множества А называется кол-во входящих в его состав различных элементов и обозначается через |А|.
Например: А={a,b,c,d} , |A|=4
§ Множество А и В называются равномощными, если между их элементами существует взаимно однозначное соответствие.
Взаимно-однозначное соответствие предполагает, что каждому элементу множества В поставлен в соответствие ровно один элемент множества А.
{0,1,2} , {лошадь, корова, телевизор} – равномощные.
6. Способы задания множества. (табличная форма или пересечение элементов, описание признака или свойства элементов множества, с помощью порождающей процедуры).
· Табличная форма или перечисление элементов
А = {a1,a2,…,an}
Пример.
Множество студентов данной группы определяется их списком в журнале.
Множество всех стран на земном шаре – их списком в атласе.
Множество всех костей человека в книге по анатомии.
· Описание признака и свойства элементов в множестве
Множество = {х| х обладает свойством Р}
/понятие свойства.
Под свойством предмета «х» будем понимать такое повествовательное предложение, в котором нечто утверждается относительно предмета «х» и которое можно характеризовать как истинное или ложное по отношению к «х».
Пример.
- Свойства быть квадратом целого числа задает (бесконечное) множество всех квадратов целых чисел.
А = {y|Е х э z & y=x2}
- свойство делиться на число 2 без остатка задается множеством чётных чисел.
В = {y|Е х э z & y=x*2}
-Свойство рост студента 180 см задает множество студентов.
В = {х|х – студент рост, которого 180 см }
· С помощью порождающей процедуры.
Каждый последующий элемент множества определяется на основании предшествующих элементов.
Пример.
- каждый последующий элемент есть сумма двух предыдущих, задается следующим образом.
D={xk | x0=0, x1=1, xk=xk-2+xk-1}
· Графическое задание множества с помощью диаграмм Эйлера – Вена
7. Понятие подмножества, надмножества.
Множество А называют подмножеством множества В, если каждый элемент множества А является так же элементом множества В.
То что множество А является подмножеством множества В обозначается
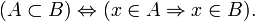
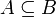так:
Если каждый элемент множества A входит во множество B, то A называется подмножеством B, а B называется надмножеством A. Пустое множество по определению считается подмножеством любого множества.
Пример.
Множество всех чётных чисел является подмножеством множества всех целых чисел, множество {1,2,3}- подмножество множества {0,1,2,3}
8. Понятие булеана множества.
· Количество всех подмножеств ( множество всех подмножеств) некоторого множества А называется его булеаном, или множеством степенью, и обозначается Р(А), В(А).
И равно 2|A| - где |A|- мощность множества А.
Пример.
А = {1,3,5}, P(А) = {0,{1},{3},{5},{1,3},{1,5},{3,5},{1,3,5}}
Кол-во собственных подмножеств некоторого множества А равно 2|A|-1.
9. Свойства теоретико-множественных отношений ( свойства отношений равенства, свойства отношения нестрогого включения, свойства отношения строгого включения).
· Свойство отношения равенства:
А=А(рефлективность);
А=В->В=А (симметричность)
А=В &В=С -> А=С (транзитивность)
· свойства отношения нестрогого и строгого включения
10. Операции над множеством
основные операции над множествами:
- пересечение:
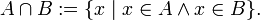
- объединение:
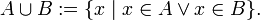
Если множества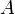 
и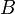 
не пересекаются: 
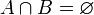, то их объединение обозначают также: 
.
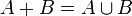- разность (дополнение):
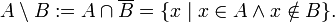
- симметрическая разность:
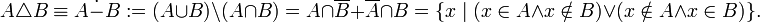
- Декартово или прямое произведение:
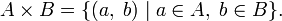
11. Понятие соответствия элементов множеств.
Определение. Соответствием между множествами А и В называется некоторое подмножество G их декартова произведения.
Если, то говорят, что соответствует при соответствии . При этом множество всех таких называют областью определения соответствия , а множество соответствующих значений называются областью значений соответствия .
В принятых обозначениях, каждый элемент , соответствующий данному элементу называется образом при соответствии , наоборот, элемент называется прообразом элемента при данном соответствии.
Соответствие называется полностью определённым, если , то есть каждый элемент множества имеет хотя бы один образ во множестве ; в противном случае соответствие называется частичным.
Соответствие называется сюръективным, если , то есть если каждому элементу множества соответствует хотя бы один прообраз во множестве .
Соответствие называется функциональным (однозначным),если любому элементу множества соответствует единственный элемент множества .
Соответствие называется инъективным, если оно является функциональным, и при этом каждый элемент множества имеет не более одного прообраза.
Соответствие называетсявзаимно-однозначным (биективным), если любому элементу множества соответствует единственный элемент множества , и наоборот. Можно сказать также, что соответствие является взаимно-однозначным, если оно является полностью определённым, сюръективным, функциональным, и при этом каждый элемент множества имеет единственный прообраз.
Пример 1: а) Англо-русский словарь устанавливает соответствие между множествами слов русского и английского языка. Оно не является функциональным, так как почти каждому русскому слову соответствует несколько английских переводов; оно, также, не является, как правило, полностью определённым соответствием, так как всегда существуют английские слова, не включённые в данный словарь. Таким образом, это частичное соответствие.
б) Соответствие между аргументами функции и значениями этой функции является функциональным. Однако оно не является взаимно-однозначным, так как каждому значению функции соответствуют два прообраза и.
в) Соответствие между расположенными на шахматной доске фигурами и занимаемыми ими полями является взаимно однозначным.