Двухточечная краевая задача

Министерство общего и профессионального образования

Российской Федерации

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ

МОРСКОЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Л.А. Руховец

ЧИСЛЕННЫЕ МЕТОДЫ

( МЕТОД СЕТОК и МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ

ДЛЯ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ)

Конспект лекций

САНКТ –ПЕТЕРБУРГ

ВВЕДЕНИЕ

Основное внимание в курсе лекций уделяется методу конечных элементов (МКЭ). Часть курса посвящена решению уравнений в частных производных методом сеток. В заключение рассмотрены методы решения интегральных уравнений. Основной подход при изложении материала – это точка зрения математика-вычислителя, а не просто пользователя. Задача курса – дать основные идеи методов, основные приложения, обратить внимание на принципиальные вопросы их применения, а также на особенности. Кроме того, рассматривается и алгоритмическая сторона методов.

Одним из самых эффективных методов решения краевых задач для уравнений в частных производных был и остается метод сеток. Основные причины этого:

- простота построения сеточных уравнений, являющихся системами линейных алгебраических уравнений;

- стандартность необходимых вычислений – простота логики, простота вычислительных алгоритмов;

- наличие эффективных итерационных методов решения систем сеточных уравнений;

- универсальность – весьма широк круг задач, к которым он применяется.

Однако в его использовании есть и ряд трудностей:

- сложность аппроксимации краевых задач с естественными краевыми условиями, сложности с аппроксимацией краевых условий на криволинейной границе, сложности с аппроксимацией уравнений высокого порядка;

- сложность установления факта сходимости во многих случаях;

- сложность построения схем повышенного порядка точности.

Результатом синтеза метода сеток и проекционных методов является метод конечных элементов (известен также под названием вариационно-разностного метода и проекционно-сеточного метода).

Наряду с методом сеток важную роль в прошлом играли проекционные методы приближенного решения уравнений в частных производных. Наиболее известны методы Ритца и Галеркина. Особое значение эти методы имели до широкого распространения компьютеров. В некоторых случаях при ручном счете они позволяли получать прекрасные результаты.

Достоинства проекционных методов известны – это воспроизведение, при этом практически автоматическое, важных свойств исходной задачи, например, таких, как симметрия, положительная определенность и т.д.; наличие техники исследования разрешимости и сходимости.

Что такое метод сеток? Кратко поясним. В области, в которой рассматривается краевая задача для дифференциального уравнения, выбирается сетка узлов (рис.1, 2). Рассмотрим примеры.

I. Краевая задача:

;

положительное целое.

Рис.1. Сетка узлов для одномерной краевой задачи

II.

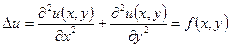в области G,

;

положительные целые,

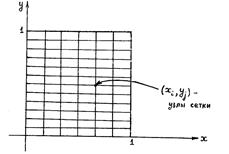
Рис.2. Сетка узлов для области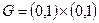

В каждом узле сетки дифференцируемое уравнение аппроксимируется разностным: производные заменяются разностными отношениями, так что вместо дифференциального уравнения получаем систему линейных алгебраических уравнений, неизвестными в которой являются значения искомого решения в узлах сетки. Таким образом, вместо краевой задачи для дифференциального уравнения возникает задача решения системы линейных алгебраических уравнений. Из приведенного объяснения понятно название метода – метод сеток.

Остановимся чуть подробнее на первом примере. Напомним известную формулу численного дифференцирования

для случая, когда имеет четыре производных; Записывая дифференциальное уравнение в узлах сетк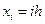и при 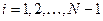и подставляя в него 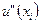с помощью этой формулы, получим

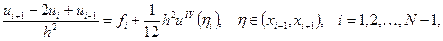
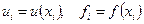
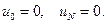
Таким образом, если считать известными, то удовлетворяют системе линейных алгебраических уравнений. К сожалению, нам неизвестны. Однако при достаточно малых 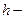шагах сетки и ограниченности функции 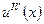добавки к правым частям в уравнениях 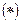можно считать малыми, и потому есть надежда, что решение системы линейных алгебраических уравнений

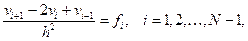
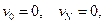
величины можно рассматривать как приближения значений точного решения в узлах сетки. Таким образом, что такое метод сеток мы пояснили с помощью примера.

Что такое проекционный метод? Мы поясним это в общей форме, так как в этом случае особенно хорошо ясна его идея.

В абстрактном гильбертовом пространстве 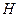со скалярным произведением рассмотрим уравнение

(1.1)

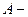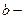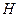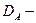где линейный оператор, известный элемент из , а искомый. Пусть область определения оператора 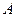в 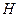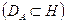. Пусть 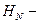конечномерное подпространство 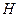, такое, что .

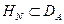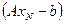Приближенным решением уравнения (1.1) назовем элемент , такой, что невязка ортогональна любому элементу 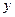из , т.е. элемент 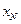, для которого выполняется условие

(1.2)

Последнее условие позволяет получить систему линейных алгебраических уравнений для нахождения 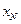. Пусть 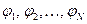образуют базис в . Приближенное решение будем искать в виде

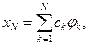
где 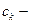неизвестные числа, 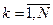. Подставляя это выражение в (1.2) и полагая 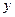последовательно равным 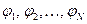, получим систему для определения параметров :

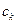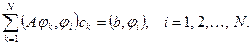(1.3)

Матрица системы линейных алгебраических уравнений имеет вид

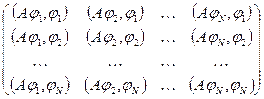
Описанный процесс отыскания приближенного решения уравнения (1.1) называется методом Галеркина. Функции 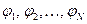называются координатными функциями (метода Галеркина) проекционного метода.

В проекционных методах стало традиционным использовать в качестве координатных функций алгебраические или тригонометрические полиномы. Однако во многих задачах оказалось, что системы линейных алгебраических уравнений, возникающие в методе Галеркина, таковы, что решить их на компьютере практически невозможно. Причина этого заключается в том, что ошибки округления ''забивают'' правильное решение. Именно данное обстоятельство затрудняло применение проекционных методов. Теоретически точность этих методов была высока, но невозможно было реализовать алгоритм на компьютере.

За последние 30 лет отношение к проекционным методом изменилось. Это связано с возникновением метода конечных элементов. Данный метод, как мы отмечали, можно рассматривать как результат синтеза двух методов – метода сеток и метода Галеркина.

В 1943 г. Р. Курант предложил использовать в методе Ритца специальные координатные функции. Оказалось, что их применение (в методе Ритца) для решения краевой задачи для уравнения Пуассона в прямоугольнике приводит к конечным системам линейных алгебраических уравнений, по структуре и свойствам совпадающим с системами, полученными методом сеток. Несколько позднее инженеры, решавшие задачи строительной механики, пришли к этому же методу иным путем. Именно у них данный метод получил название ''метод конечных элементов''. Математическая суть метода очень кратко, хотя и не очень полно и точно может быть выражена так:

МКЭ – это проекционный метод со специальными координатными функциями.

В чем специфика координатных функций МКЭ? Рассмотрим метод Галеркина и предположим, что координатные функции метода ортогональны в следующем смысле

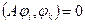при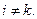

В этом случае очевидно, что матрица метода Ритца будет диагональной и отыскание решения в этой ситуации элементарно.

Основная особенность координатных функций МКЭ состоит в том, что каждая координатная функция ортогональна всем остальным за исключением некоторого конечного числа, не зависящего от их общего числа.

Это очень важное обстоятельство приводит к тому, что матрицы систем сеточных уравнений оказываются разреженными. Они ''почти'' диагональные. Именно это обстоятельство и определяет близость вычислительных свойств метода сеток и МКЭ.

ДВУХТОЧЕЧНАЯ КРАЕВАЯ ЗАДАЧА

Краевая задача для линейного обыкновенного дифференциального уравнения второго порядка является простой, но достаточно содержательной моделью более сложных задач, на примере которой можно осветить многие аспекты как МКЭ, так и метода сеток.

Проекционные методы, и в частности МКЭ, часто удобнее применять не к самим дифференциальным уравнениям непосредственно, а к равносильным вариационным или обобщенным их формулировкам.