Числовые характеристики случайных величин

Как уже неоднократно упоминалось, законы распределения несут полную информацию о случайной величине. Однако на практике, приступая к изучению СВ, исследователь часто не знает её закон распределения. Кроме этого, часто бывает достаточным знать не полную, а лишь частичную информацию о случайной величине. Такую информацию и доставляют числовые характеристики СВ. Рассмотрим наиболее важные и применяемые.

Определение 1. Математическое ожидание 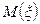случайной величины 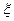называется число определяемое формулами:

для ДСВ, заданной своим рядом распределения

, (20)

для НСВ с помощью её плотности вероятности

(21)

Отметим простейшие свойства математического ожидания.

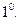Механический смысл математического ожидания.

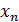Представим себе отрезок числовой

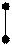
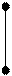
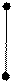
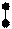
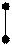
прямой, на которой помечены значения

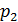ДСВ 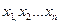, как стержень, на который в

точках 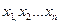подвешены грузы

Рис. 15 величиной соответственно

Такая механическая система имеет точку равновесия (рис.15). Эта точка равновесия и есть 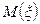. Таким образом, механический смысл математического ожидания – это среднее взвешенное значений ДСВ, весами являются соответствующие вероятности. Ясно, что 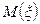всегда находится внутри диапазона изменения ДСВ. Для НСВ смысл тот же, только стержень надо представить неоднородным – его плотность в каждой точке определяется функцией .

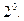Если .

.

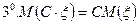Определение 2. Дисперсия СВ есть число, которое вычисляется по формулам:

для ДСВ: D 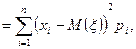(22)

для НСВ: D 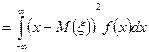(23)

Для краткости обозначим и отметим простейшие свойства дисперсии.

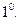Из определения дисперсии

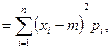D D

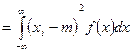
видно, что дисперсия характеризует разброс (рассеивание) значений СВ около своего математического ожидания. Из этих формул также видно, что дисперсия имеет размерность квадрата значений СВ. Поэтому для характеристики разброса значений СВ около своего среднего значения удобнее применять характеристику 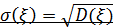, которая называетсясредним квадратическим отклонением.

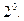D(С) = 0

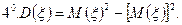Эту формулу удобно использовать при вычислениях.

Пример 36. (тест). Если график функции распределения НСВ имеет

вид, изображённый на рисунке, то

1 математическое ожидание 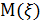равно…

Варианты ответа: 1) ¾, 2) ¼, 3) 3/2,

0 1 2 x 4) 2/3, 5) 5/4.

Решение. F(x) = ax + b – линейная функция, проходящая через две точки (1,0) и (2,1) Итак, F(x) = x-1, точнее

Пример 37. В связке имеется 4 различных ключа, из которых только одним можно открыть дверь. Наудачу выбирается ключ и делается попытка открыть им дверь. Если ключ не подходит, он больше не используется. Построить ряд и функцию распределения числа использованных ключей. Найти числовые характеристики. Найти вероятность того, что а) дверь будет открыта вторым ключом; б) будет использовано не менее двух ключей.

Решение. Начнём с обозначений. Обратимся к вопросу примера и сразу поймём, что речь идёт о СВ 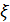= (число использованных ключей). Ясно, что эта ДСВ может принимать значения 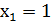(сразу выбрали нужный ключ), (первый ключ не подошёл, а второй подошёл), 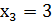и

Для составления ряда распределения вычислим соответствующие вероятности. Нетрудно видеть, что

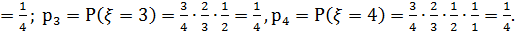Получили ряд распределения.

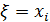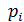	1/4	1/4	1/4	1/4

F(x)

Далее строим функцию распределения и её график.

3/4

1/4

а

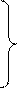
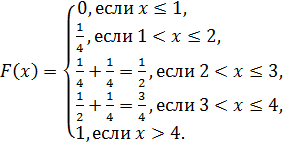½ б)

0 1 2 3 4

По ряду распределения вычислим числовые характеристики.

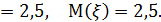
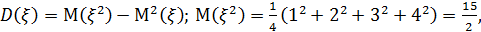следовательно, 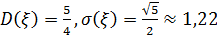- среднее квадратическое отклонение.

В примере требуется найти вероятности: а)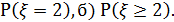

а) По ряду распределения легко видеть, что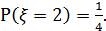

б) По ряду распределения также нетрудно подсчитать: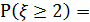

Обе вероятности показаны и на графике F(x).

Пример 38. В системе координат 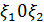наудачу брошена точка в квадрат Для случайной величины 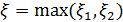найти F(x), f(x), числовые характеристики. Вычислить вероятность того, что максимальная координата точки окажется в интервале 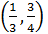и вероятность отклонения максимальной координаты точки от своего математического ожидания на величину .

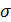Решение. Сделаем чертёж.

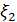
=x

Воспользуемся определением

1 А B функции распределения

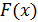х = P(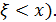

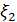=x Для нашего примера получаем

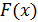0 х С 1 =P

Рис.16

Рассмотрим формулу более подробно.

Во-первых,

Прямая , биссектриса I координатного угла, делит наш квадрат на два треугольника. Треугольник ОАВ составляют точки, удовлетворяющие неравенству 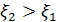, противоположному неравенству 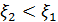удовлетворяют точки треугольника ОВС. Итак,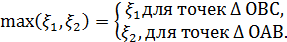

Тогда

Возьмём на чертеже на обеих осях координат некоторое значение 0<x<1 и рассмотрим два случая.

1) Для точек 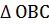найдём вероятность

2) Прямая 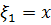разбивает треугольник на две части. Неравенству 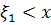удовлетворяют точки, расположенные левее прямой (заштрихованная часть ).

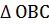3) Для точек 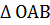аналогично получаем, что неравенству

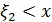соответствует заштрихованная часть этого треугольника.

Объединяя оба случая, видим, что неравенству, соответствует заштрихованная часть квадрата. Поэтому, вспоминая геометрические вероятности, получаем

.

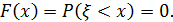Итак, если 0<x<1, то Далее очевидно, что если < 0, то - невозможное событие и Если 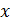> 1, то - достоверное событие и Окончательно получаем:

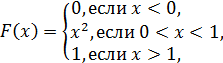
Находим числовые характеристики.

,

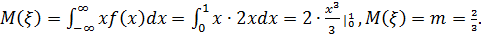
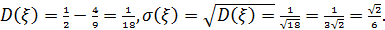
Вычисляем указанные в задании вероятности.

)= )

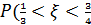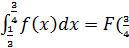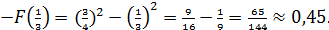
Графики и изображены на рис. 17,18.

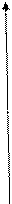
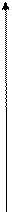
1 2

C B F(3/4) B

F(1/3) A

A

0 1/3 ¾ 1 x 0 1/3 ¾ 1 x

Рис.17 Рис.18

Полученную вероятность можно показать геометрически. На рис.17 она равна длине отрезка АВ на оси ординат; на рис.18 она равна площади трапеции АВСД.

т.е. приблизительно 63% значений этой СВ оказывается в окрестности своего матожидания радиуса СКО