Тема 1.4. Преобразование координат на плоскости. Элементарная теория линий второго порядка

Простейшими преобразованиями координат на плоскости есть пре­образование поворота и параллельного переноса. Одна и та же точка имеет различные координаты в разных системах декартовых коорди­нат. Существует связь между координатами точки в различных системах координат.

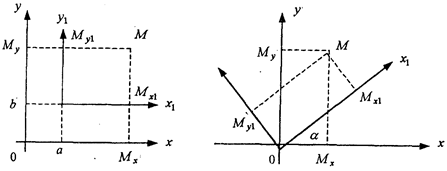
Рис.1.4.1 Рис.1.4.2

Параллельный перенос. Заданы две системы координат: старая ОХУ

и новая О₁Х₁У₁ (рис . 1. 4 .1) . Начало новой системы координат находится в точке O₁(а,в) .

Старые координаты х, у точки М через новые координаты x₁y₁ вы­ражаются формулами

x=x₁ +a, y=y₁+b (1.4.1)

откуда х₁ =х-а, y₁ =y- b, (1.4.2)

Поворот координатных осей. Новая система координат OX₁Y₁ полу­чена поворотом старой на угол α вокруг точки О (рис.1.4.2).Старые координаты х, у точки М через новые координаты x₁, y₁ выражаются фор­мулами

x=x₁cosα - y₁sinα

y=x₁sinα + y₁cosα (1.4.3)

В общем случае, когда заданы преобразования параллельного переноса и поворота осей координат, связь между старыми и новыми координа­тами имеет вид:

x=x₁cosα - y₁sinα+a; y=x₁sinα + y₁cosα+b (1.4.4)

Студент должен уметь общее уравнение кривой второго порядка

a₁₁х² + 2а₁₂ ху + а₂₂ у² + c₁x + с₂ у + d = 0, (1.4.5)

путем преобразования системы координат (параллельный перенос, по­ворот) приводить к простейшему (каноническому) уравнению.

В новой системе координат уравнением кривой (1.4.5) будет одно из следую­щих канонических уравнений:

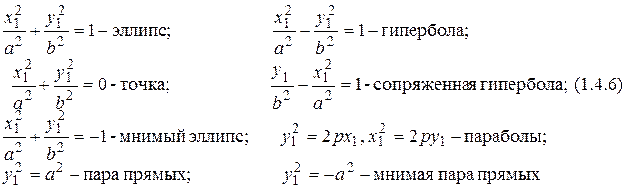Общее уравнение второй степени (1.4.5) при повороте осей ко­ординат на угол α преобразуется в уравнение

a΄₁₁х₁² + а΄₂₂ у₁² + c΄₁x₁ + с΄₂ у₁ + d΄ = 0 (1.4.7)

формулы преобразования координат имеют вид (1.4.3), угол α опре­деляется по формуле

Уравнение (1.4.7) приводится к каноническим уравнениям (1.4.6) выделением полных квадратов и применением фoрмул парал­лельного переноса (1.4.1) .

Пример 1.4.1.Кривая второго порядка задана уравнением

Зх² +4xy-4x-8y= 0

Записать каноническое уравнение этой линии. В данном случае а₁₁ = 3, 2а₁₂ = 4, a₂₂ = 0 . По формуле (1.4.8) находим ctg2α=3/4 > 0 . Сле­довательно,

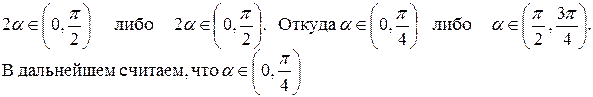
Тогда sinα >0 и cosα >0, cos2α >0. По формулам (1.4.9) вычисляем

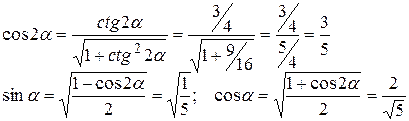
Замечание: если предположить, что

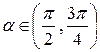
то sinα > 0, cosα < 0, cos2α < 0 и по формулам (1.4.9) имеем:

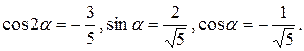
Вычисленные значения sinα и cosα подставляем в (1.4.3):

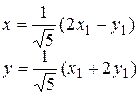
Подставим полученные выражения в исходное уравнение и преоб­разуем его.

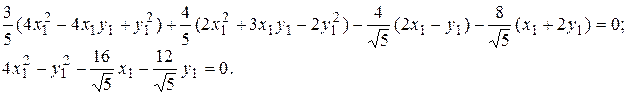
В последнем уравнении выделим полные квадраты

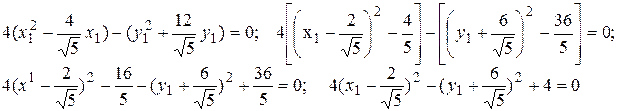
Используя формулы (1.4.1), положим

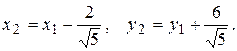
В новых координатах последнее уравнение имеет вид

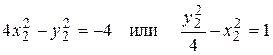
Это уравнение определяет сопряженную гиперболу (действительная ось ОУ) с полуосямиа=1, b=2.

Построим гиперболу в новой системе координат O₁Х₂У_2. Вначале вы­числим старые координаты точки O₁ в которой находится центр гиперболы.

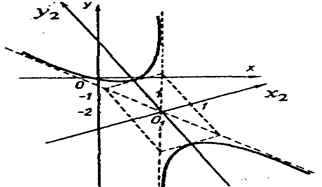
Рис.1.4.3

Для этой точки х₂ = 0; у₂ = 0.По формулам (1.4.1) находим

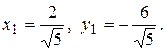
С помощью формул (1.4.3) вычисляем

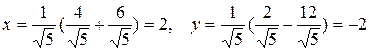
Так, точка O₁ имеет координаты O₁ (2,-2).Через точку O₁ проводим ось OX ₂ , для которой tgα = 1/2 и ось OY₂ перпендикулярно оси OX₂. Строим гиперболу

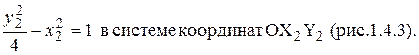
Вопросы для самопроверки

1.Дайте определение эллипса, гиперболы, параболы.

2.Дайте определение директриссы и эксцентриситета кривых второго порядка.

3. Какие линии определяют уравнения 9х² ± 4у²= 36 . Вычислите параметры кривых.

4.Получите уравнения асимптот гиперболы.

5.Чему равен эксцентриситет для окружности?

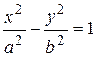6.Докажите, что произведение расстояний от произвольной точки гиперболы до ее асимптот есть величина постоянная.