Оценка устойчивости по ЛЧХ

Построение амплитудно-фазовых частотных характеристик разомкнутых систем связано с громоздкими вычислениями, поэтому целесообразно оценивать их устойчивость по логарифмическим частотным характеристикам. Для этого необходимо построить ЛЧХ разомкнутой системы (рис.5.14).

На рис.5.14 условно показано четыре варианта возможного прохождения ЛФХ. В том случае, когда АФЧХ не имеет точек пересечения с вещественной осью слева от точки с координатами (-1, j0), то для устойчивости замкнутой системы необходимо и достаточно, чтобы выполнялось условие ωс< ωкр. То есть замкнутая система будет абсолютно устойчивой, если ЛАХ разомкнутой системы принимает отрицательные значения раньше, чем ЛФХ достигнет значения фазы -1800 (кривая 4

на рис.5.14).

Если ЛАХ разомкнутой системы принимает отрицательные значения позже, чем ЛФХ достигнет значения фазы -1800 (кривая 1 на рис.5.14), то замкнутая система неустойчивая.

Если ЛАХ разомкнутой системы принимает значение амплитуды 0 дб на одной

частоте, что и ЛФХ достигнет значения фазы -1800 (кривая 2 на рис.5.14), то это соответствует колебательной границе устойчивости.

В условно устойчивых системах (кривая 3 на рис.5.14) для оценки устойчивости следует в диапазоне частот, где ЛАХ больше нуля, подсчитать число переходов ЛФХ через прямую -1800. Если число положительных (сверху вниз) переходов через эту

прямую равняется числу отрицательных (снизу вверх), то система в замкнутом состоянии устойчива.

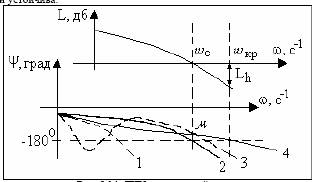
Рис. 5.14. ЛЧХ разомкнутой системы:

1 - система неустойчива;

2 - система нейтральная;

3 - система условно устойчивая;

4 - система абсолютно устойчивая

По ЛЧХ разомкнутой системы можно определить запасы устойчивости: запас по фазе µ отсчитывается по ЛФХ на частоте среза ωс, а запас по амплитуде Lh соответствует значению ЛАХ на критической частоте ωкр, взятому с обратным знаком (кривая 4 на рис.5.14).

Если ωс=ωкр, то система находится на границе устойчивости.

Граничное значение общего коэффициента передачи разомкнутой системы kгр определяется из выражения

20 lg kгр = 20 lg k + Lh, (5.16) где k - общий коэффициент передачи разомкнутой системы. В заключение дадим некоторые рекомендации, которые следуют из практики проектирования систем. Во-первых, для того чтобы в системе были обеспечены

необходимые запасы устойчивости, наклон ЛАХ в диапазоне частот, в котором расположена частота среза, должен быть равным -20дб/дек. При наклоне характеристики, равном -40дб/дек, трудно обеспечить необходимый запас устойчивости по фазе. При наклоне характеристики, равном 0 дб/дек, получают излишне большие запасы устойчивости по фазе, система становится передемпфированной с длительным переходным процессом. Во-вторых, запас устойчивости по фазе в системе зависит от диапазона частот, в котором ЛАХ разомкнутой системы на частоте среза имеет наклон -20дб/дек. Чем больше этот

диапазон частот, тем выше запас устойчивости по фазе и наоборот.

ВОПРОС№3

Анализ качества переходных процессов линейных САУ.

Общие понятия

Качество представляет собой комплексную оценку работы системы управления, включающую устойчивость, точность, быстродействие и зависящую от назначения системы. Устойчивость системы обеспечивает затухание переходных процессов с течением времени, т.е. обеспечивает принципиальную возможность прихода системы в некоторое установившееся состояние при любом внешнем воздействии. Однако далее требуется, во-первых, чтобы это установившееся состояние было достаточно близко к заданному и, во-вторых, чтобы затухание переходного процесса было достаточно быстрым, а отклонения при этом были бы невелики. Качество работы любой системы управления в конечном счете определяется величиной ошибки, равной разности между требуемым и действительным

значениями управляемой величины: x(t)=g(t)−y(t).

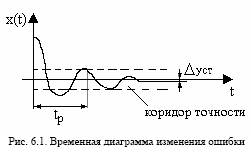
Характер процесса изменения ошибки, представленного на рис.6.1, позволяет сделать вывод об устойчивости системы, так как процесс сходится, оценить точность работы системы по величине установившейся ошибки ∆уст =x(∞) и оценить

быстродействие системы по времени регулирования tр, то есть времени, за которое ошибка системы достигает допустимое значение и при дальнейшем росте времени не превышает его. Процесс изменения ошибки во времени определяется решением дифференциального уравнения динамики замкнутой системы

Знание мгновенного значения ошибки в течение всего времени работы системы дает возможность наиболее полно судить о ее свойствах. Однако ошибка системы зависит не только от характеристик самой системы, но и от свойств, действующих на нее воздействий. Вследствие случайности задающего g(t) и возмущающего f(t) воздействий такой подход не может быть реализован. Поэтому приходится оценивать качество системы управления по некоторым ее свойствам, проявляющимся при различных типовых воздействиях. Для определения качественных показателей системы управления в этом случае используются так называемые критерии качества.

В настоящее время разработано большое число различных критериев качества, с помощью которых оценивается либо точность системы в установившемся состоянии, либо качество переходного процесса.

Точность системы задается и определяется в установившихся режимах величиной установившейся ошибки. Для анализа качества переходного процесса существует три основных вида приближенных оценок: частотные, корневые, нтегральные.

ВОПРОС№6

Синтез линейных систем регулирования.

Задачи синтеза сводятся к следующему: нужно спроектировать систему автоматического регулирования для заданного объекта так, что бы система в целом обеспечивала выполнение заданных качественных показателей (допустимое время регулирования, точность поддержания заданной величины). Это сводится к нахождению корректирующего устройства.

Типы корректирующих устройств .

Последовательное корректирующие устройство.

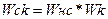
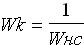
идеальное корект. Звено не применяют

Параллельное корректирующие устроиство.

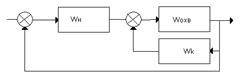
Параллельная коррекция повышает стабильность характеристик охваченных обратной связью.

Синтез линейных систем по ЛАЧХ

Построение желаемой ЛАЧХ

1) низкочастотная часть. Наклон –Y*20дб/дек (где Y – степень астотизма кол-во интегрирующих звеньев), через точку ω=1 L(1)=20lgK, К- обший коэффициент усиления всей системы .

При Y=0 проводится горизонтальная прямая L=20lgK

2) Среднечастотная часть лежит в интервале (ω2 ωср) (ωср ω3) Эта область характеризует устойчивость, быстродействие и форму переходного процесса. ωср-частота среза такая при которой 20lg(Wp* ωср)=0 – наклон -20дб/дек ωср=1/τ

интервал (ω2 ωср) (ωср ω3) выбирается в пределах 0,2-0,9 декадычем больше интервал тем больше запас по фазе

Сопряжение низко и средне частотного участка производится прямой с наклоном –(40-60)дб/дек

3) Высокочастотная часть для частот больше ω3 проводидится по возможности с наклоном, равным наклону характеристики исходной системы обычно –(40-60)дб/дек .

Синтез последовательного корректирующего устройства

1 построить желаемую ЛАЧХ

2 построить ЛАЧХ исходной системы

3 вычисть из ЛАЧХ желаем ЛАЧХ исходной получится ЛАЧХ корект устройства

4 подобрать по таблице электрическую схему.

Синтез параллельного корректирующего устройства

ВОПРОС№5

Критерий устойчивости Найквиста.

ВОПРОС№6

Критерий устойчивости Михайлова.