Прогнозирование роста числа правонарушений

Статистические данные роста тяжких преступлений по России приведены в таблице:

Год
ЧП

Средствами Excel по этим экспериментальным значениям построить теоретическую функцию роста тяжких преступлений и вычислить прогнозируемую численность тяжких преступлений в России в начале 2004 года. Результаты расчета и сравнения теории и эксперимента представить в виде диаграммы Excel.

Указания:

Для решения задачи необходимо выбрать функцию, выражающую зависимость роста тяжких преступлений от времени. Вид этой функции зависит от многих факторов (экономики, политической обстановки, морали, права и т.д.), поэтому очевидно, что чем больше неопределенных параметров будет иметь математическая модель, Прогнозирование роста числа правонарушений - student2.ru , тем точнее будет соответствующий прогноз.

Ограничимся сначала случаем всего двух параметров и зададим вид этой функции формулой экспоненциальной регрессии Прогнозирование роста числа правонарушений - student2.ru . Коэффициенты регрессии 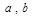определяются на основе статистического анализа следующим образом:

1. В любых двух свободных ячейках (например, A1, B1) заносятся произвольные допустимые значения параметров 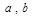Прогнозирование роста числа правонарушений - student2.ru .

2. К столбцу с экспериментальными значениями таблицы добавляется столбец вычисляемых по формуле Прогнозирование роста числа правонарушений - student2.ru теоретических значений.

3. Составляется столбец отклонений теории от эксперимента.

4. Составляется столбец квадратов этих отклонений.

5. Квадраты отклонений суммируются в свободную нижнюю ячейку, в которой образуется величина, зависящая от 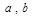Прогнозирование роста числа правонарушений - student2.ru .

6. Решение задачи выполняется с помощью программы-надстройки Поиск решения (В качестве целевой ячейки указывается ячейка с суммой квадратов отклонений, в качестве изменяемых ячеек – ячейки содержащие параметры 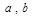Прогнозирование роста числа правонарушений - student2.ru , режим решения – минимальное значение).

Эта программа находит значения 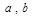Прогнозирование роста числа правонарушений - student2.ru , при которых сумма квадратов отклонений будет наименьшей и вычисляет число тяжких правонарушений в 2004 году.

Примечание: В исходной таблице размещаются достаточно большие числа (годы и численность преступлений). Для того чтобы не оперировать большими числами следует добавить в таблицу столбец, в котором значения (Год) уменьшены в 100 раз, и столбцы, в которых значения (ЧП Эксперимент) и (ЧП Теория) уменьшены в 1000 раз. Пункты статистического анализа 2 – 6 следует проводить именно для этих столбцов и по ним же следует строить диаграмму. Диаграмму следует строить по столбцам (ЧП Эксперимент) и (ЧП Теория), а в качестве подписи оси абсцисс использовать столбец (Год).

Образец таблицы

		a	b
		10,765	0,478

Год	Год	ЧП Данные	ЧП Теория	ЧП Данные	ЧП Теория	Квадраты отклонений
	19,70			130,789	131,739	0,903
	19,85			139,456	141,527	4,289
	19,90			148,321	144,949	11,372
	19,91			148,987	145,643	11,183
	19,92			148,951	146,340	6,815
	19,93			148,351	147,041	1,715
	19,94			148,311	147,746	0,320
	19,95			147,987	148,453	0,217
	19,96			147,564	149,164	2,560
	19,97			147,147	149,878	7,461
	19,98			147,787	150,596	7,892
	20,04				154,976
					Сумма	54,728

Сравнительная диаграмма теории и эксперимента должна иметь вид:

Прогнозирование роста числа правонарушений - student2.ru

Кроме рассмотренной экспоненциальной регрессии удобно пользовать регрессией в виде многочлена. Решите самостоятельно Задание 2.11, используя при этом многочлен третьей степени вида: 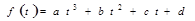Прогнозирование роста числа правонарушений - student2.ru . Сравните на диаграмме результаты прогноза по двум регрессиям с экспериментом.