Классификация систем эконометрических уравнений
Система уравнений в эконометрических исследованиях может быть построена по-разному.
Возможна система независимых уравнений, когда каждая зависимая переменная 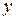 рассматривается как функция одного и того же набора факторов
рассматривается как функция одного и того же набора факторов 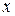 :
:
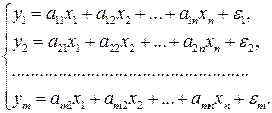 (2.1)
(2.1)
Для нахождения его параметров используется метод наименьших квадратов. По существу, каждое уравнение этой системы является уравнением регрессии. Так как фактические значения зависимой переменной отличаются от теоретических на величину случайной ошибки, то в каждом уравнении присутствует величина случайной ошибки 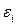 .
.
Если зависимая переменная 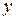 одного уравнения выступает в виде фактора
одного уравнения выступает в виде фактора 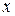 в другом уравнении, то исследователь может строить модель в виде системы рекурсивных уравнений:
в другом уравнении, то исследователь может строить модель в виде системы рекурсивных уравнений:
 (2.2)
(2.2)
В данной системе зависимая переменная 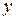 включает в каждое последующее уравнение в качестве факторов все зависимые переменные предшествующих уравнений наряду с набором собственно факторов
включает в каждое последующее уравнение в качестве факторов все зависимые переменные предшествующих уравнений наряду с набором собственно факторов 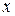 . Каждое уравнение этой системы может рассматриваться самостоятельно, и его параметры определяются методом наименьших квадратов (МНК).
. Каждое уравнение этой системы может рассматриваться самостоятельно, и его параметры определяются методом наименьших квадратов (МНК).
Наибольшее распространение в эконометрических исследованиях получила система взаимозависимых уравнений. В ней одни и те же зависимые переменные в одних уравнениях входят в левую часть, а в других уравнениях – в правую часть системы:
 (2.3)
(2.3)
Система взаимозависимых уравнений получила название системы совместных, одновременных уравнений. В эконометрике эта система уравнений называется также структурной формой модели. В отличие от предыдущих систем каждое уравнение системы одновременных уравнений не может рассматриваться самостоятельно, и для нахождения его параметров традиционный МНК неприменим. С этой целью используются специальные приемы оценивания.
В рассмотренных классах систем эконометрических уравнений структура матрицы коэффициентов при зависимых переменных различна.
Представим систему эконометрических уравнений в матричном виде:
BY + ГX = E,
где B – матрица коэффициентов при зависимых переменных;
Y – вектор зависимых переменных;
Г- матрица параметров при объясняющих переменных;
X - вектор объясняющих переменных;
E – вектор ошибок.
Если матрица В диагональная, то рассматриваемая модель является системой независимых уравнений. Так, при трех зависимых и трех объясняющих переменных модель имеет вид:
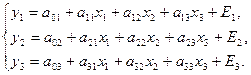
Матрица параметров при зависимых переменных является диагональной:
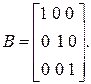
Если матрица В треугольная (или может быть приведена к такому виду), то модель представляет собой систему рекурсивных уравнений. Так, если модель имеет вид:
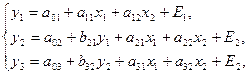
т.е. зависимая переменная y1 первого уравнения участвует как объясняющая переменная во втором уравнении системы, а зависимая переменная y2 второго уравнения рассматривается как объясняющая переменная в третьем уравнении. Тогда матрица коэффициентов при зависимых переменных модели составит:
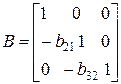 ,
,
т.е. представляет собой треугольную матрицу.
Если матрица В не является ни диагональной, ни треугольной, то модель представляет собой систему одновременных уравнений. Так, для модели вида
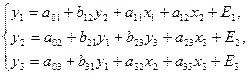
получим матрицу коэффициентов при зависимых переменных:
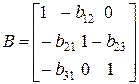 ,
,
которая не является ни диагональной, ни треугольной. Соответственно то отражается на выборе метода оценки параметров эконометрических систем.
