Автоматные грамматики: способы построения детерминированного КА (ДКА) по заданному НКА
а) Заносим в таблицу переходов все состояния, заданные НКА;
б) Строим подмножество состояний для каждого состояния;
в) Если при построении подмножеств в пункте б) не появилось новое подмножество, то построение таблицы закончено;
г) Если при построении подмножеств появились новые подмножества, то эти подмножества принимаем в качестве новых состояний искомого автомата, заносим их в таблицу переходов и повторяем пункт б);
дано НКА: 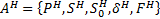 , построить ДКА
, построить ДКА 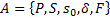 .
.
1) Пусть 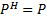 ;
;
2) Распишем множество всевозможных состояния для какого-то состояния 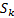 , оно будет выглядеть как:
, оно будет выглядеть как: 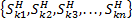 , каждому такому подмножеству множество состояний НКА поставим в соответствие одно состояние искомого
, каждому такому подмножеству множество состояний НКА поставим в соответствие одно состояние искомого 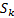 .
.
3) Определим множество заключительных состояний искомого ДКА: 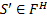 и
и 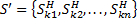 , то
, то 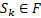 .
.
4) 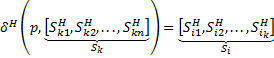 ,
, 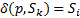
Автоматные грамматики: приведение некоторых языков грамматик к автоматному виду.
Язык называется конечным, если он состоит из конечного числа конечных слов.
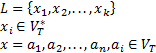
Утверждение: любой конечный язык порождается автоматной грамматикой. Пусть задан некоторый конечный язык 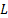 , введем
, введем  нетерминал и построим правила грамматики в следующем виде:
нетерминал и построим правила грамматики в следующем виде:
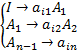
Последовательно применяя эти правила можно вывести цепочку 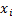 . Применяя описанную теорию ко всем цепочкам языка, получим автоматную грамматику, порождающую данный язык.
. Применяя описанную теорию ко всем цепочкам языка, получим автоматную грамматику, порождающую данный язык.
Конечный преобразователь: определение
КП представляет собой конечный автомат, к которому добавлена выходная лента, неограниченная с обоих сторон. На эту ленту происходит запись выходных символов.
Пусть конечный преобразователь 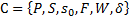 , где
, где 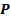 - входной алфавит,
- входной алфавит, 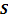 - алгоритм состояний,
- алгоритм состояний, 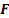 - алфавит заключительных состояний,
- алфавит заключительных состояний, 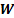 - выходной алфавит,
- выходной алфавит, 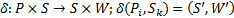 .
.
Конфигурация КП:  , где
, где 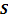 - состояния конечного преобразователя,
- состояния конечного преобразователя,  - входная цепочка,
- входная цепочка, 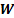 - выходная цепочка. Работу КП можно представить в виде смены конфигураций. Переход от
- выходная цепочка. Работу КП можно представить в виде смены конфигураций. Переход от 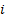 к
к 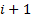 есть такт работы конечного преобразователя.
есть такт работы конечного преобразователя.
Для любой автоматной грамматики можно простроить конечный преобразователь, формирующий на выходе синтаксический разбор цепочек, порождаемых заданной грамматикой.
Контекстно-свободные грамматики (КС): определение, приведенная КС-грамматика, неукорачивающая КС-грамматика, КС-грамматика без цепных правил, КС-грамматика без леворекурсивных правил. Преобразования КС-грамматик.
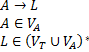
Символ 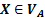 называется непроизводящим, если в заданной грамматике из него невозможно вывести терминальную цепочку.
называется непроизводящим, если в заданной грамматике из него невозможно вывести терминальную цепочку.
Символ 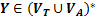 называется недостижимым, если он не может появиться ни в одной выводимой цепочке.
называется недостижимым, если он не может появиться ни в одной выводимой цепочке.
Символ 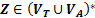 называется бесполезным, если он непроизводящий и недостижимый.
называется бесполезным, если он непроизводящий и недостижимый.
КС-грамматика называется приведенной, если она не содержит бесполезных символов.
