Классы интегрируемых функций 4 страница

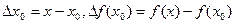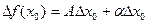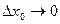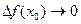Положим .Тогда определение дифференцируемости в точке можно записать в виде .Видно, что функция , дифференцируемая в точке , непрерывна в этой точке, поскольку при имеем . Поделим наше равенство на 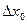. Получим

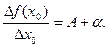
Следовательно, 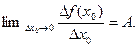Этот предел называется производной функции в точке и обозначается одним из следующих символов: 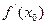или 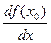.Верно и обратное: если у функции в точке существует производная, то функция в этой точке дифференцируема. Действительно, если производная существует, то 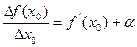, где 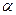- б.м. при 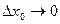. Следовательно, 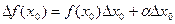, что и требовалось. Сформулируем доказанное как отдельную теорему.

Теорема 5.1. Для того, чтобы функция была дифференцируемой в точке , необходимо и достаточно, чтобы она имела там производную.

Определение 5.2.Дифференциалом функции в точке называется произведение .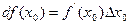

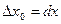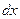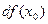Если - независимая переменная, полагают ; не зависит от точки .Дифференциал линейно зависит от 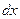. Его называют главной линейной частью приращения функции в точке .(Главной, потому что при 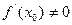оставшаяся часть приращения функции, равная 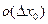стремится к 0 быстрее дифференциала).

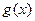Теорема 5.2. Пусть и дифференцируемы в точке . Тогда

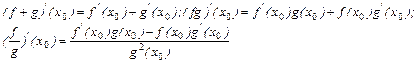
(Последняя формула верна при ).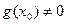

Доказательство. Докажем последнее утверждение; остальные доказать ещё проще, а схема доказательства сохраняется. Имеем

.

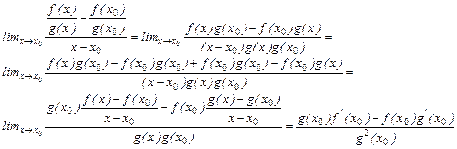Заметим, что мы имеем право писать 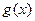в знаменателе, так как согласно с леммой о сохранении знака 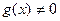в некоторой окрестности точки , и можем переходить к пределу в сумме (в числителе) и дроби по свойствам функций, имеющих в предел.

Теорема доказана.

Теорема 5.2’.В условиях теоремы 5.2 имеем

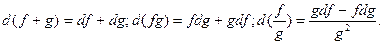
Доказательство. Умножим равенства предыдущей теоремы на .

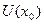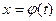Теорема 5.3(о дифференцируемости сложной функции). Пусть определена в некоторой окрестности точки , , и дифференцируема в самой точке , а функция определена в окрестност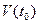и точки 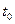, причём (а) 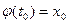, ,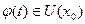и(б) при 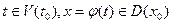. Тогда сложная функция, 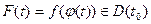и .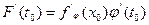

Следует заметить, что и 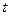меняются в разных пространствах вещественных чисел!

Доказательство. Поскольку 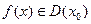, имеем 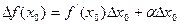,где 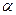- б.м. при 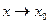. Аналогично, поскольку 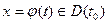, имеем 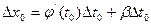, где 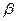- б.м. при 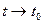.Объединяя эти результаты, получим

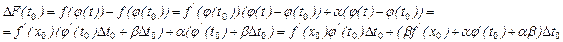При 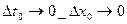,так как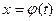 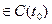. Значит выражение в скобках при 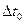является б.м. Теорема доказана.

Рассмотрим дифференциал функции 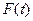в точке 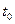. По определению, он равен 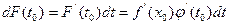. Но 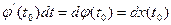.В этом случае 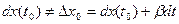, но всё равно имеем 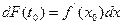, т.е. дифференциал функции как функции от 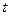ищется по той же формуле, что и дифференциал функции 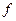как функции от .Это свойство называется инвариантностью формы первого дифференциала при замене переменной.

Теорема 5.3’.Первый дифференциал функции 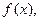вычисляется по формуле 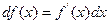независимо от того, будет независимой переменной или нет.

Это свойство очень важно при при вычислении интегралов. Оно не имеет места для дифференциалов высших порядков в общем случае.

6.Теоремы о дифференцируемых функциях.

Определение 6.1.Функция называется дифференцируемой на множестве 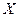,если она дифференцируема 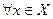.Это обозначается так: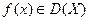

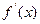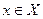Производная для в этом случае является функцией от . Если эта функция является дифференцируемой на 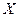, то её производная называется второй производной функции .Обозначение: 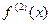. Вообще

Определение 6.2.Если 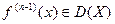, то, по определению, 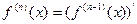.Для в этом случае пишут .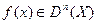

Определение 6.3.Если 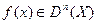, то .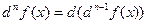

Рассмотрим теперь вопрос об инвариантности .Если - независимая переменная, то 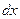- не зависит от , и 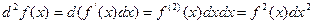(и вообще, 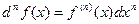).Если 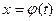, то 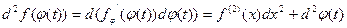.Значит, если 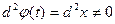, инвариантности нет.

Теорема 6.1.Дифференциалы высших порядков не инвариантны, вообще говоря, относительно замены переменной.

Определение 6.4 Пусть функция определена на интервале 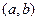. Точка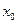 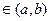называется точкой локального максимума функции , если существует окрестность 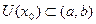, для всех точек которой 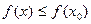.Точка называется точкой строгого локального максимума, если для всех точек окрестности .

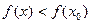Определение 6.5.При тех же условиях на функцию , точка называется точкой локального минимума функции , если для всех точек некоторой окрестности выполняется неравенство 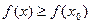, и точкой строгого локального минимума , если последнее неравенство – строгое.

Определение 6.6.Точки локального максимума или минимума называются точками локального экстремума.

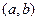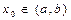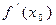Теорема 6.2.(Ферма).Пусть функция определена и дифференцируема на интервале и - точка экстремума для . Тогда = 0.

Доказательство. Предположим для определённости, что - точка локального максимума. Пусть 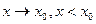.Имеем

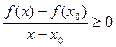.Значит, 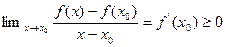. Пусть теперь 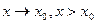.Рассматривая то же отношение, получим 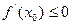.Следовательно, 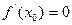. Теорема доказана.

Теорема 6.3 (Ролля). Пусть 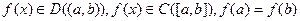.Существует 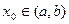такая, что .

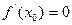Доказательство.1.Если - константа, то 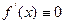, и теорема верна. 2.Если функция -не константа, то ,во всяком случае, она непрерывна на 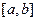(поскольку дифференцируема).Но тогда она достигает где-то на 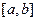своего максимума и минимума. Хотя бы одна из этих точек не будет совпадать 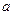ни с ,ни с 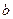, и потому расположена на 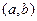.Значит, она будет точкой локального экстремума, и производная в ней будет равна нулю. Теорема доказана.

Теорема 6.4(Коши). Пусть 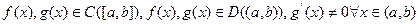. Тогда существует точка 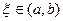, для которой

.

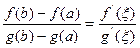Доказательство.1.Заметим, что 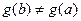, так как в противном случае по теореме Ролля нашлась бы точка 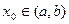, в которой 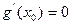.2. Для функции

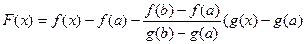
на 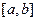выполнены все условия теоремы Ролля. Найдётся по этой теореме точка 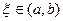, в которой 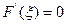.Имеем

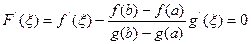; поделив на 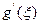,получим что требовалось доказать.

Следствие 6.4.1.(Теорема Лагранжа). Пусть 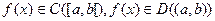.Существует 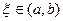, для которой

.

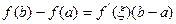Доказательство. Достаточно взять 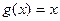в предыдущей теореме.

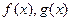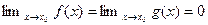Следствие 6.4.2.(«Простое» правило Лопиталя). Пусть функции определены в проколотой(и может быть односторонней) окрестности точки и (1) ;(2) 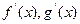определены в той же окрестности, и (3) 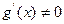;(4)пусть существует 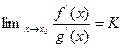.Тогда .

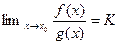Доказательство. Пусть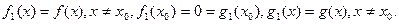

Функции 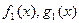удовлетворяют условиям теоремы Коши .Значит,

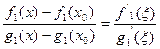для некоторой точк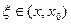и .При 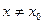функци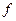и и 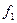совпадают, так что полученное равенство можно переписать как

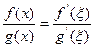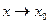. При имеем 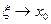, теорема доказана.

Аналогичная теорема верна для неопределённости 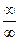, но её мы доказывать не будем. Желающие могут найти её в 1-ом томе «толстого» Фихтенгольца.

Следствие 6.4.3(Формула Тэйлора с остаточным членом в форме Пеано).Пусть функция имеет производные всех порядков до ( 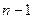)-го включительно в некоторой окрестности 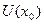и производную 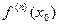в самой точке . Тогда для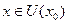

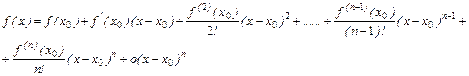
Доказательство. Вычислим предел:

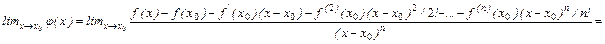(Легко видеть, что к данной дроби применимо правило Лопиталя. Применяя его ( 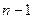) раз, получим)

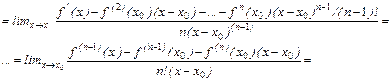
(Функция 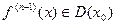,значит 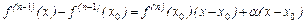,где 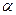- б.м.; )

.

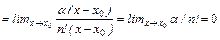Теорема доказана.

Разность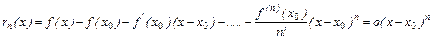

называется остаточным членом формулы Тэйлора в форме Пеано. Ниже, при более жёстких ограничениях на функцию , мы получим форму остаточного члена, более удобную в приложениях.

6.5.Остаточный член в форме Шлёмильха – Роша и его варианты.

Пусть функция определена на отрезке 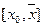и имеет там непрерывные производные порядков до 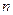включительно, и пусть в интервале 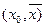у неё есть конечная 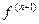. Пусть 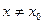- некоторая точка этого интервала Рассмотрим функцию

, .

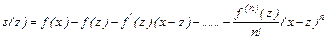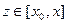Эта функция непрерывна на 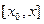и имеет внутри него конечную производную. Кроме того, 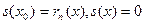.Если вычислить производную в точке 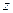, получим

.

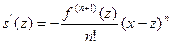Пусть теперь 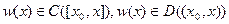- любая функция, для которо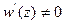й при 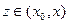.По теореме Коши, для 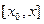имеем

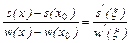,где 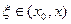или, что то же самое, 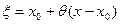, 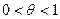.Подставляя в эту формулу 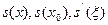, после умножения на 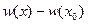, получим

.

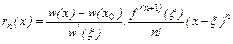Полагая 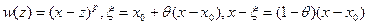, получим

.

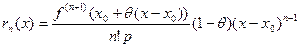Такая форма остаточного члена называется формой Шлёмильха – Роша.

Если известны какие-нибудь ограничения на модуль производных независимо от их порядка, такая форма позволяет оценивать величину остаточного члена для конкретных

Особенно употребительны два частных случая. При 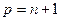получаем остаточный член в форме Лагранжа

.

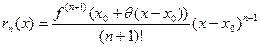При 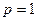получаем остаточный член в форме Коши

.

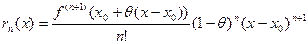Полученные формы остаточного члена позволяют более точно оценивать разность 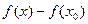, если известно ,например, что модуль производных ограничен какой-либо константой.

Теорема 6.6.Если функция 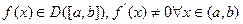, то обратная функция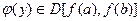

Доказательство. При рассмотрении непрерывных функций было доказано, что если на отрезке задана строго монотонная функция, то на области её значений определена однозначно обратная к ней функция, которая будет строго монотонной и непрерывной. Из условий теоремы 6.6 следует, что строго монотонна. Поэтому существование и непрерывность 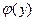доказывать не нужно. Имеем