Приближенное решение дифференциального уравнения по методу Эйлера
Кафедра математики
Методические указанияи задания к выполнению
расчетно-графической работы по теме:
"Приближенные методы решения
дифференциальных уравнений"
для студентов всех специальностей и всех направлений подготовки бакалавров очной формы обучения
Брянск 2015
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное
учреждение высшего образования
«Брянский государственный инженерно-технологический университет»
Кафедра математики
УТВЕРЖДЕНЫ
научно-методическим
советом университета
Протокол № ____
oт “____”___________2015 г.
Методические указанияи задания к выполнению
расчетно-графической работы по теме:
"Приближенные методы решения
дифференциальных уравнений"
для студентов всех специальностей и всех направлений подготовки бакалавров очной формы обучения
Брянск 2015
Составители: доцент Камозина О.В.,
доцент Котова И.А.
Рецензент:
профессор кафедры «Физика», д. ф.-м. н. Евтюхов К.Н.
Рекомендованы редакционно-издательской и методической комиссиями механико-технологического факультета БГИТУ.
Протокол № 1 от 10.09.2015 г.
Приближенные методы решения дифференциальных уравнений
Решение многих дифференциальных уравнений нельзя свести к интегрированию известных функций. Поэтому важное значение приобретают приближенные методы решения.
Существуют два метода численного решения дифференциальных уравнений 1-го порядка: метод Эйлера и метод Рунге-Кутта.
Метод Эйлера
Для данного уравнения 1-го порядка
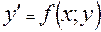 (1)
(1) 
можно составить таблицу приближенных значений частного решения, удовлетворяющего начальному условию
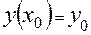 (2)
(2)
или приближенно вычертить интегральную кривую на некотором отрезке[ 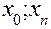 ].
]. 
По методу Эйлера данный отрезок [ 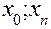 ] разбивается точками
] разбивается точками  на n частичных отрезков.
на n частичных отрезков.
На первом частичном отрезке [ 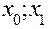 ] искомая интегральная кривая, проходящая через известную точку M0(
] искомая интегральная кривая, проходящая через известную точку M0( 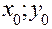 ) заменяется касательной к ней в точке
) заменяется касательной к ней в точке 
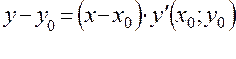 ,
,
Откуда при 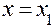 получается приближенное значение
получается приближенное значение  искомого решения уравнения в точке
искомого решения уравнения в точке 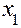
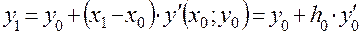 .
.
Далее тем же способом для отрезка [ 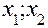 ] находим приближенное значение
] находим приближенное значение  искомого решения в точке
искомого решения в точке 
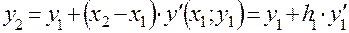 .
.
Продолжая этот процесс, последовательно находим приближенные значения 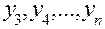 искомого решения в точках
искомого решения в точках 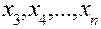 .
.
С увеличением 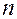 , при достаточно малой длине частичных отрезков, этим методом можно достигнуть заданной точности решения.
, при достаточно малой длине частичных отрезков, этим методом можно достигнуть заданной точности решения.
Данный отрезок [ 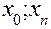 ] удобно разделить на частичные отрезки одинаковой длины
] удобно разделить на частичные отрезки одинаковой длины
 (шаг).
(шаг).
Тогда все последовательные приближенные значения 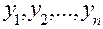 решения уравнения (1),удовлетворяющего начальному условию (2), вычисляются по рекуррентной формуле
решения уравнения (1),удовлетворяющего начальному условию (2), вычисляются по рекуррентной формуле
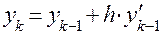 .
.
Таким образом, по методу Эйлера интегральную кривую, проходящую через точку  , заменяют ломаной (ломаной Эйлера), каждый отрезок которой проведен по направлению поля, определенного уравнением (1).Иными словами, от предыдущей вершины ломаной к последующей двигаются по касательной к интегральной кривой, проведенной через начальную точку каждого отрезка.
, заменяют ломаной (ломаной Эйлера), каждый отрезок которой проведен по направлению поля, определенного уравнением (1).Иными словами, от предыдущей вершины ломаной к последующей двигаются по касательной к интегральной кривой, проведенной через начальную точку каждого отрезка.
Недостатки метода Эйлера:
1. Малая точность при значительном шаге 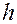 и большой объем работ при малом шаге.
и большой объем работ при малом шаге.
2. Систематическое накопление ошибок.
Поэтому метод Эйлера применяют лишь для грубых приближений.
Расчет ведется по следующей схеме:
 |  |  | 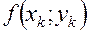 | 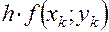 |
 | 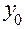 |  | 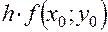 | |
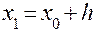 | 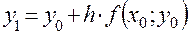 |  | 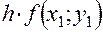 | |
 |  |  | 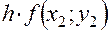 | |
| … | … | … | … | … |
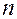 -1 -1 | 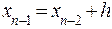 |   | 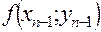 |  |
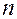 |  | 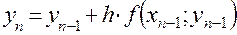 |
Метод Рунге-Кутта
Метод Рунге-Кутта более чаще употребляется,чем метод Эйлера, хотя и требует большего объёма вычислений, однако это окупается повышенной точностью, что даёт возможность проводить счет с большим шагом, т.е. для получения результатов с одинаковой точностью в методе Эйлера потребуется значительно меньший шаг, чем в методе Рунге-Кутта.
Геометрически этот метод для задачи (1),(2) также как и в методе Эйлера состоит в том, что на малом отрезке [ 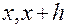 ] интегральная кривая
] интегральная кривая 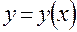 уравнения (1) заменяется прямой, проходящей через точку
уравнения (1) заменяется прямой, проходящей через точку 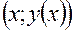 , однако в основу положен более тонкий, чем в методе Эйлера, подход к определению направления этого отрезка прямой.
, однако в основу положен более тонкий, чем в методе Эйлера, подход к определению направления этого отрезка прямой.
Обозначим через 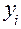 приближенное значение искомого решения в точке
приближенное значение искомого решения в точке  . По методу Рунге-Кутта вычисление приближенного значения
. По методу Рунге-Кутта вычисление приближенного значения 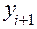 в следующей точке
в следующей точке  производится по формулам:
производится по формулам:

где
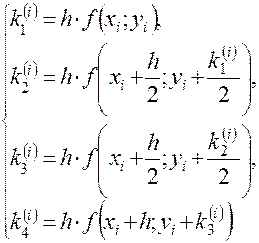 (3)
(3)
Шаг расчета можно поменять при переходе от одной точки к другой. Для контроля правильности выбора шага 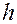 рекомендуем вычислить дробь
рекомендуем вычислить дробь
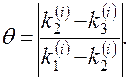
Величина 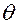 не должна превышать нескольких сотых. В противном случае шаг
не должна превышать нескольких сотых. В противном случае шаг 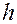 следует уменьшить.
следует уменьшить.
Все вычисления удобно располагать по схеме:
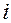 |  | 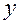 | 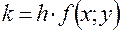 |  |
 | 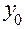 |  |  | |
 | 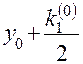 |  | 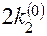 | |
 | 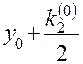 | 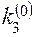 |  | |
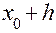 | 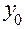 + + 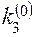 | 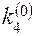 | 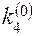 | |
 | ||||
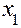 |  | 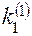 | 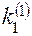 | |
| … | … | … | … | … |
Порядок заполнения таблицы:
1) Записываем в первой строке таблицы данные значения 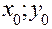 .
.
2) Вычисляем 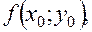 умножаем на
умножаем на 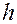 и заносим в таблицу в качестве
и заносим в таблицу в качестве  .
.
3) Записываем во второй строке таблицы  .
.
4) Вычисляем 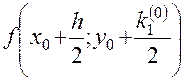 , умножаем на
, умножаем на 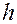 и заносим в таблицу в качестве
и заносим в таблицу в качестве  .
.
5) Записываем в третьей строке таблицы 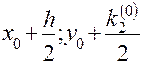 .
.
6) Вычисляем 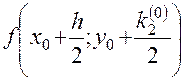 , умножаем на
, умножаем на 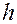 , заносим в таблицу в качестве
, заносим в таблицу в качестве 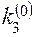 .
.
7) Записываем в четвертой строке таблицы 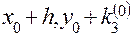 .
.
8) Вычисляем 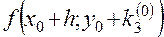 , умножаем на
, умножаем на 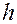 и заносим в таблицу в качестве
и заносим в таблицу в качестве 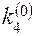 .
.
9) В столбец  записываем
записываем  .
.
10) Суммируем числа, стоящие в столбце  , делим на 6 и заносим в таблицу в качестве
, делим на 6 и заносим в таблицу в качестве  .
.
11) Вычисляем  .
.
Затем все вычисления продолжают в том же порядке, принимая за начальную точку  .
.
Содержание РГР "Приближенные методы решения дифференциальных уравнений"
Студенту предлагается выполнить следующую работу:
1 . Точное решение дифференциального уравнения.
2. Приближенное решение дифференциального уравнения методом Эйлера.
3. Приближенное решение дифференциального уравнения методом Рунге-Кутта.
Варианты и образец выполнения РГР приведены ниже.
Варианты
1) 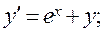


 .
.
2) 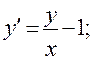

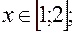
 .
.
3) 

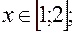
 .
.
4) 
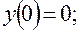

 .
.
5) 
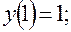
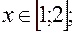
 .
.
6) 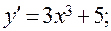
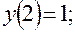

 .
.
7) 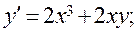
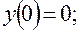

 .
.
8) 

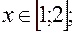
 .
.
9) 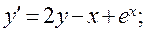
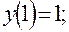
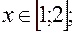
 .
.
10) 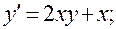


 .
.
11) 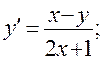
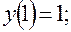
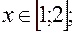
 .
.
12) 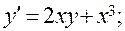


 .
.
13) 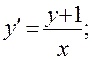

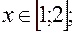
 .
.
14) 
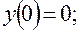

 .
.
15) 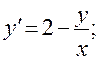


 .
.
16) 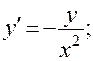
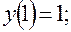
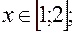
 .
.
17) 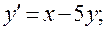
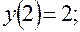

 .
.
18) 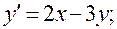
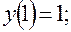
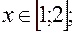
 .
.
19) 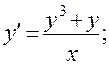
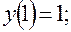
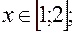
 .
.
20) 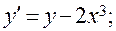
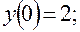

 .
.
21) 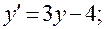


 .
.
22) 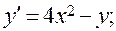
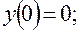

 .
.
23) 
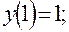
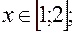
 .
.
24) 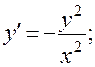
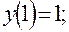
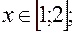
 .
.
25) 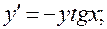


 .
.
26) 
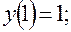
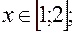
 .
.
27) 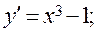


 .
.
28) 


 .
.
29) 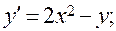
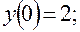

 .
.
30) 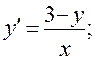
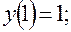
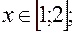
 .
.
Образец выполнения РГР
Задание. Найти решение дифференциального уравнения  с начальным условием
с начальным условием  на отрезке
на отрезке  , приняв за шаг
, приняв за шаг 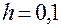 .
.
Точное решение
 -линейное уравнение.
-линейное уравнение.
Подстановка: 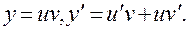


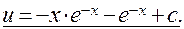

При  найдем
найдем 
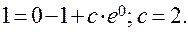
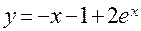 - точное решение дифференциального уравнения.
- точное решение дифференциального уравнения.
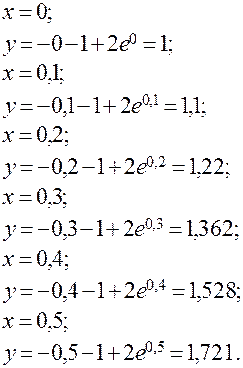
Приближенное решение дифференциального уравнения по методу Эйлера
Т.к. 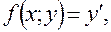 то
то 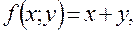

 |  | 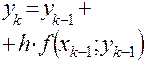 | 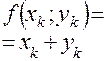 | 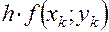 |
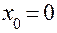 |  |  | 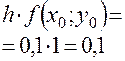 | |
 | 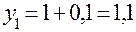 | 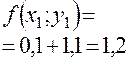 |  | |
 | 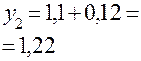 |  | 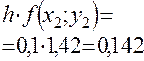 | |
 | 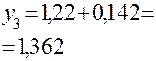 | 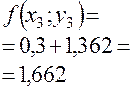 | 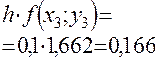 | |
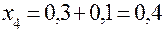 | 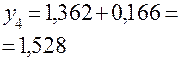 | 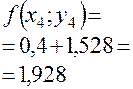 | 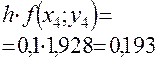 | |
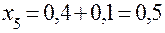 |  |
