Определитель второго порядка

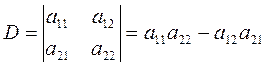
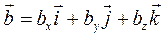2. Скалярным произведением двух векторов и называется число, определяемое равенством

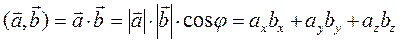(1)

где 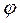- угол между векторами и .

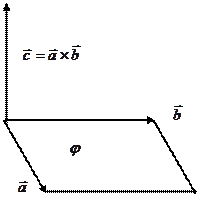Рис. 1

Рис. 2

3. Векторным произведением двух векторов и называется вектор , длина которого равна произведению длин векторов-сомножителей на синус угла между ними и который направлен перпендикулярно векторам и так, что векторы , , образуют правую тройку (рис. 1):

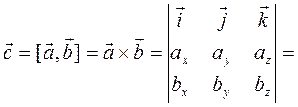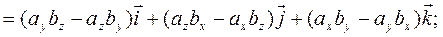(2)

Геометрически равен площади S параллелограмма, построенного на век­торах и :

4. Смешанное произведение трех векторов есть число, равное

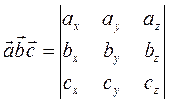(3)

Модуль смешанного произведения равен объему параллелепипеда, построенного

на векторах , , .

5. Общее уравнение плоскости Р имеет вид

Ax + By + Cz + D = 0,

где 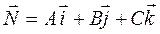-нормальный вектор плоскости (рис. 2).

Уравнение плоскости, проходящей через три заданные точки М₀(x₀,y₀,z₀), М₁(x₁,y₁,z₁), и М₂(x₂,y₂,z₂) имеет вид

(4)

Угол между двумя плоскостями, имеющими нормальные векторы и , определяется как угол между и 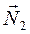; косинус этого угла находится по формуле

(5)

6. Уравнения прямой в пространстве, проходящей через две заданные точкиМ₀(x₀,y₀,z₀) и М₁(x₁,y₁,z₁)имеют вид

(6)

7. Матрицей размера называется прямоугольная таблица чисел, состоящая из т строк и n столбцов:

Произведением матрицы размера на матрицу размера называется матрица размера cэлементами

(7)

(поэлементное умножение i-й строки матрицы Aна k-й столбец матрицы B).

Матрица размера 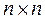называется квадратной матрицей n-го порядка. Эле­менты образуют главную диагональ матрицы. Определитель, составленный из элементов квадратной матрицы, называется определителем мат­рицы н обозначается или .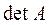

Матрица Е с элементами называется единичной матрицей n-го порядка.

Матрица называется обратной к матрице если

(8)

Элементы обратной матрицы вычисляются по формулам

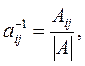(9)

где 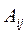- алгебраическое дополнение элемента 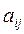, матрицы 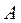, а -ее опреде­литель.

8. Матрица 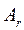называется канонической, если в начале ее главной диагонали стоят единицы, а все остальные элементы равны нулю; например,

Любая матрица А может быть приведена к каноническому виду 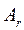путем элементарных преобразований: а) перестановки столбцов (строк); б) умножения столбца (строки) на число, отличное от нуля; в) прибавления к элементам какого-либо столбца (строки) соответствующих элементов другого столбца (стро­ки), умноженных на число.

Матрицы, переходящие друг в друга в результате элементарных преобразова­ний, называются эквивалентными: ~ .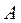

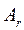Число г единиц, стоящих на главной диагонали канонической матрицы 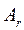не зависит от способа приведения матрицы А к каноническому виду и называется рангом исходной матрицы A: r(A)=r. Эквивалентные матрицы имеют один и тот же ранг.

9. Система трех линейных уравнений с тремя неизвестными х₁, х₂,

х₃ имеет вид

(10)

где 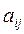- коэффициенты системы; - свободные члены. Определитель третьего порядка 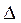, составленный из коэффициентов при неизвестных, называется опреде­лителем системы. Если , то единственное решение системы (10) выражается формулами Крамера:

(11)

где - определители третьего порядка, получаемые из определителя системы 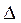заменой 1, 2 или 3-го столбца соответственно свободными членами .

Систему (10) можно записать матричной форме: , где