Характеристическое уравнение СП и ее устойчивость

Характеристическое уравнение СП

Рассмотрим математическую модель одноосной силовой СП (2.18), в которой напряжение, приложенное к обмоткам СД, обозначим как

,

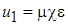где 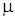– коэффициент усиления, 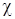– крутизна датчика угла.

Запишем (2.18) в операторной форме. При этом будем считать, что датчик моментов отключен, т. е. 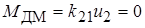. Тогда получим:

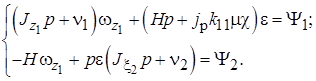(3.1)

Решим уравнение (3.1) относительно 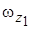и 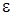. Воспользуемся формулами Крамера:

, .

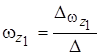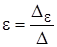После вычисления определителей 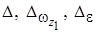будем иметь:

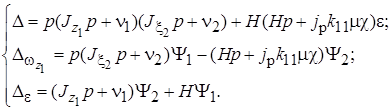(3.2)

Определитель 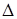из системы (3.2) преобразуем следующим образом:

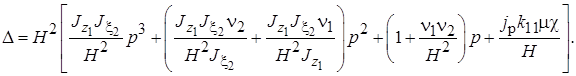
Обозначим:

; ; ; ; .

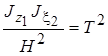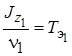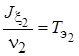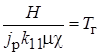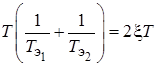Физический смысл величин следующий: 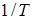– круговая частота нутационных колебани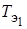й; и 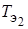– постоянные времени платформы и кожуха гироскопа с невращающимся ротором; 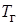– постоянная времени прецессионного движения платформы; 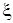– коэффициент демпфирования.

Характеристическое уравнение получим, приравняв 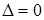. Пренебрегая малой величиной 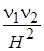, получим систему третьего порядка:

.

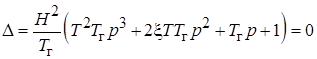Для исследования устойчивости разработана специальная методика – диаграмма Вышнеградского. Необходимо данное уравнение привести к виду

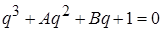. (3.3)

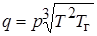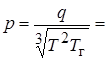
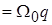Для этого сделаем замену переменной: или , где 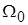– среднегеометрический корень, который является характеристикой скорости (быстроты) протекания переходного процесса в системе. В автоматике заменой 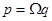можно перейти к новой комплексной переменной.

Коэффициенты 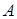и 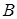в (3.3) будут иметь вид

, , .

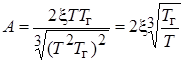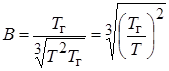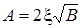Условие устойчивости системы: 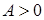, 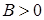и 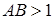. Уравнение границы устойчивости: .

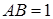Медленное приведение ОСП(Медленное приведение СП; Время медленного приведения

Схема начальной выставки

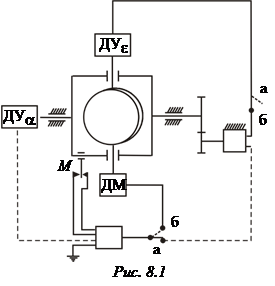Погрешность выставки приводит к погрешностям платформы. Время определяет готовность к работе. Существуют следующие виды выставки: а) быстрое приведение – размыкается цепь обратной связи, маятник управляет двигателем (рис. 8.1); б) медленное (точное) приведение – цепь стабилизации замкнута, управление на ДМ; в) комбинированная.

Источниками информации об угловом положении СП могут быть ДУα, автоколлиматоры, гониометрические схемы; маятники, акселерометры, гироинтеграторы, астрокорректоры и др.

Время приведения определяется выражением:

,

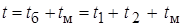где 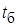– время быстрого приведения; 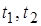– время первого и второго этапов

быстрого приведения соответственно; 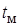– время медленного приведения.

Медленное приведение

На этапе медленного приведения замыкается цепь стабилизации и на ДМ подается управляющий момент 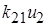. Если характеристика маятника зависит от 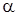(или используется ДУαдля выставки СП в ее нулевое положение), то получим линейную характеристику с насыщением.

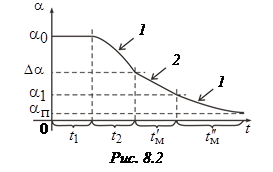
Общий вид 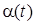представлен на рис. 8.2, где 1 – экспоненциальная зависимость; 2 – линейная зависимость.

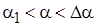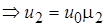На участке имеем , на 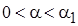получаем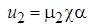 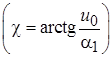. Уравнение движения примет вид

.

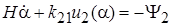Время медленного приведения определяется как

.

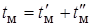На участке 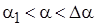получим 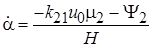. Обычно .

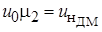Время на данном участке находится по формуле:

,

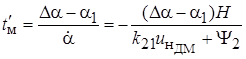где .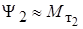

На участке 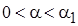получим 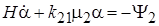. Решение имеет вид

;

,

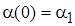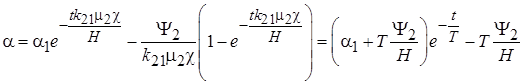где .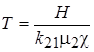

Время приведения платформы в пороговое положение 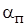, при котором 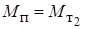, определяется при 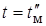. Получим

; .

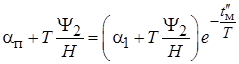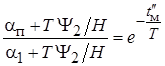Откуда определяется время :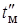

.

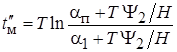Движение возможно пока .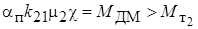

[1]Далее в тексте индекс «с» опускается.