Экономико-математическая модель транспортной задачи
Н.Е. Гучек
Доцент, кандидат технических наук
КОНСПЕКТ ЛЕКЦИЙ
по дисциплине
Методы оптимальных решений
Часть 3
Направление подготовки: 080100 «Экономика»
Профили подготовки: «Финансы и кредит», «Бухгалтерский учет, анализ и
аудит»
Форма обучения: очная и заочная
Тула 2015 г.
Конспект лекций подготовлен доцентом Н.Е. Гучек и обсужден на заседании кафедры «Финансы и менеджмент» факультета ЭиМ,
протокол № 1 от 30 августа 2013 г.
Зав. кафедрой __________________________Е.А. Федорова
Конспект лекций пересмотрен и утвержден на заседании кафедры «Финансы и менеджмент» факультета права и управления
протокол №__1_ от_августа___2015_ г.
Зав. кафедрой __________________________Е.А. Федорова
Содержание
Лекция 1. Транспортная задача. 4
1.1.Экономико-математическая модель транспортной задачи. 4
1.2. Нахождение первоначального базисного распределения поставок. 6
1.3. Решение транспортной задачи методом потенциалов. 7
Лекция 2. Особые случаи транспортной задачи. 13
2.1. Вырожденность в транспортных задачах. 13
2.2. Открытая транспортная задача. 15
Лекция 3. Элементы теории игр. 20
3.1. Основные понятия теории игр. 20
3.2. Примеры игр. 22
3.3. Классификация игр. 27
Лекция 4. Игры двух лиц с нулевой суммой. 29
4.1. Основные предположения для игр двух лиц с нулевой суммой. 29
4.2. Смешанные стратегии. 31
4.3. Аналитическое решение игры 2´2. 34
4.4. Доминирование стратегий. 37
Лекция 5. Графическое решение игр. 39
5.1. Графическое решение игр размерности 2´n. 39
5.2. Графическое решение игр размерности m´2. 42
Лекция 6. Решение матричных игр с помощью линейного программирования. 43
6.1. Связь матричных игр и линейного программирования. 43
6.2. Алгоритм решения матричных игр с помощью линейного программирования. 46
Лекция7. Игры с природой. 48
7.1. Критерии оптимальности в играх с природой. 48
7.2. Пример игры с природой. 50
Лекция 8. Применение теории игр в экономике. 54
8.1. Кооперативные игры.. 54
8.2. Позиционные игры.. 60
9.1. Общая постановка задачи динамического программирования. 60
Лекция 10. Применение динамического программирования в экономике. 63
10.1. Задача об инвестировании предприятий. 63
10.2. Задача о замене оборудования. 72
Библиографический список. 77
Лекция 1. Транспортная задача
План.
1.1.Экономико-математическая модель транспортной задачи.
1.2. Нахождение первоначального базисного распределения поставок.
1.3. Решение транспортной задачи методом потенциалов.
Экономико-математическая модель транспортной задачи
Транспортная задача – одна из распространенных задач линейного программирования. Ее цель – разработка наиболее рациональных путей и способов транспортирования товаров, устранение чрезмерно дальних, встречных, повторных перевозок. Все это сокращает время продвижения товаров, уменьшает затраты предприятий, связанные с осуществлением процессов снабжения сырьем, материалами, топливом, оборудованием и т.д.
В общем виде транспортную задачу можно представить следующим образом: в m пунктах производства А1, А2, ¼, Аm имеется однородный груз в количествах соответственно а1, а2, ¼, аm. Этот груз необходимо доставить в n пунктов назначения В1, В2, ¼, Вn в количествах, соответственно b1, b2, ¼, bn. Стоимость перевозки 1 ед. груза (тариф) из пункта Аi в пункт Bj равна сij ден. ед.
Требуется составить план перевозок, позволяющий вывезти все грузы, полностью удовлетворить потребителей, и имеющий минимальную стоимость.
В зависимости от соотношения между суммарными запасами груза и суммарными потребностями в нем транспортные задачи могут быть закрытыми и открытыми.
Определение 1. Если сумма запасов груза равна суммарной потребности в нем:
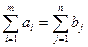 ,
,
то транспортная задача называется закрытой.
Определение 2. Если сумма запасов груза не равна суммарной потребности в нем:
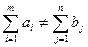 ,
,
то транспортная задача называется открытой.
Рассмотрим закрытую транспортную задачу. Обозначим xij – количество груза, перевозимого из пункта Аi в пункт Bj.
Математическая модель транспортной задачи имеет вид
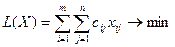
при ограничениях:
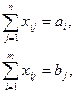
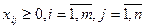 .
.
Оптимальным решением является матрица
 ,
,
удовлетворяющая системе ограничений и обеспечивающая минимум целевой функции.
Транспортная задача как задача линейного программирования, может быть решена симплексным методом, однако наличие большого числа переменных и ограничений делает вычисления громоздкими. Поэтому для решения транспортных задач разработан специальный метод, имеющий те же этапы, что и симплексный метод, а именно:
1) нахождение исходного опорного решения;
2) проверка этого решения на оптимальность;
3) переход от одного опорного решения к другому.
Рассмотри каждый из этапов.
