Производная и дифференциал. Глава 2. Дифференциальное исчисление функций одной переменной
Глава 2. Дифференциальное исчисление функций одной переменной
1.1 Производная функции в точке
Пусть функция f определена в некоторой окрестности  точки х0 , х0
точки х0 , х0 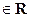 , и пусть х – произвольная точка из этой окрестности, отличная от х0 . Отношение
, и пусть х – произвольная точка из этой окрестности, отличная от х0 . Отношение  называют разностным отношением для функции f в точке х0 . Очевидно, на это отношение можно смотреть как на функцию аргумента х, определенную в проколотой окрестности
называют разностным отношением для функции f в точке х0 . Очевидно, на это отношение можно смотреть как на функцию аргумента х, определенную в проколотой окрестности 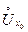 .
.
Определение. Если существует 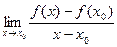 (т.е. если этот предел равен некоторому вещественному числу), то это число называют производной функции f в точке х0 .
(т.е. если этот предел равен некоторому вещественному числу), то это число называют производной функции f в точке х0 .
Производную функции f в точке х0 обозначают символами  и
и 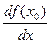 .
.
Итак, по определению

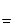
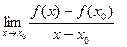 ,
,
если этот предел существует.
Укажем на одну из возможных интерпретаций введенного математического понятия. Рассмотрим движение материальной точки вдоль некоторой прямой. Обозначим через S(t) путь, пройденный точкой с момента начала движения t= 0 до момента t >0. Тогда путь, пройденный точкой за промежуток времени между моментами t0 и t , 0 < <t0 < t, равен S(t) - S(t0). В механике отношение  называют средней скоростью движения за промежуток времени между моментами t0 и t, а
называют средней скоростью движения за промежуток времени между моментами t0 и t, а  - мгновенной скоростью движения в момент t0 . Следовательно, в данном случае производная
- мгновенной скоростью движения в момент t0 . Следовательно, в данном случае производная 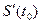 есть мгновенная скорость движения в момент t0 . В более широком плане, если две переменные у и х связаны функциональной зависимостью y = f(x), то число
есть мгновенная скорость движения в момент t0 . В более широком плане, если две переменные у и х связаны функциональной зависимостью y = f(x), то число  характеризует “скорость” изменения переменной у относительно переменной х при х=х0.
характеризует “скорость” изменения переменной у относительно переменной х при х=х0.
Разность х-х0 будем называть приращением аргумента х в точке х0 и обозначать через  , а также через h: х - х0 =
, а также через h: х - х0 =  = h. Разность f(x) – f(x0) будем называть приращением функции f в точке х0 и обозначать через
= h. Разность f(x) – f(x0) будем называть приращением функции f в точке х0 и обозначать через  , а также через
, а также через  ( h). Так как х = =х0 +
( h). Так как х = =х0 +  = х0 + h, можем записать
= х0 + h, можем записать
 =
= 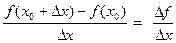 ,.
,.  =
= 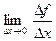 ,
,
или:
 =
=  ,
,  ==
== 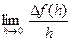 .
.
Таким образом, используя введенные выше термины производную  можно определить как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю.
можно определить как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю.
Приведем примеры вычисления производной.
Пример 1. Пусть функция тождественно в некоторой окрестности точки х0 , х0  , равна константе:
, равна константе:  Для всякого х, принадлещащего
Для всякого х, принадлещащего  и отличного от х0
и отличного от х0  =
=  = 0; поэтому
= 0; поэтому 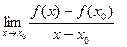 = 0, т.е.
= 0, т.е.  = 0.
= 0.
Пример 2. Пусть f(x) = a 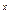 , где a> 0, a ≠ 1. Вычислим
, где a> 0, a ≠ 1. Вычислим  , где х0 - -любое вещественное число. Имеем:
, где х0 - -любое вещественное число. Имеем:  ( h) = f(x0+h) – f(x0) = a
( h) = f(x0+h) – f(x0) = a  - a
- a  = = a
= = a  ( a
( a  - 1) . Значит,
- 1) . Значит,  =
= 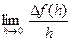 = a
= a 
 = a
= a  lna.
lna.
Пример 3. Пусть f(x) = cosx, a х0 - любое вещественное число. Тогда  ( h) = cos(x0+h) - cosx0 = -2 sin(x0+
( h) = cos(x0+h) - cosx0 = -2 sin(x0+ 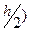 sin
sin 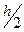 . Отсюда:
. Отсюда:
 =
= 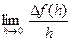 = -
= - 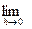 sin(x0+
sin(x0+ 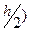
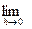
 = - sinx0 .
= - sinx0 .
Пример 4. Пусть f(x) = sinx,a х0 - любое вещественное число. Тогда  ( h) = sin(x0+h) - sinx0 = 2 cos(x0+
( h) = sin(x0+h) - sinx0 = 2 cos(x0+ 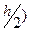 sin
sin 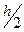 . Отсюда:
. Отсюда:
 =
= 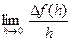 =
= 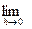 cos(x0+
cos(x0+ 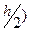
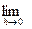
 = cosx0 .
= cosx0 .
Пример 5. Пусть f(x) =х  , где μ – некоторое вещественное число, а х0 > 0. Имеем:
, где μ – некоторое вещественное число, а х0 > 0. Имеем:  ( h) = f(x0+h) – f(x0) = (х0+h)
( h) = f(x0+h) – f(x0) = (х0+h)  - х0
- х0  = х0
= х0 
 . Отсюда:
. Отсюда:
 =
= 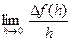 = х0
= х0 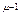
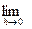
 = μ х0
= μ х0 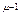 .
.
Замечание. Если показатель μ таков, что функция f(x) =х  определена и при отрицательных x (например, если μ
определена и при отрицательных x (например, если μ  ), то, повторив приведенные выше выкладки, получим для всякого x0 < 0:
), то, повторив приведенные выше выкладки, получим для всякого x0 < 0:  = μ х0
= μ х0 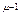 .
.
Производная  существует не всегда.
существует не всегда.
Пример 6. Пусть f(x) = х 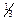 . Эта функция определена на всей числовой оси, и в силу примера 5 и замечания к нему при всяком x0 ≠ 0
. Эта функция определена на всей числовой оси, и в силу примера 5 и замечания к нему при всяком x0 ≠ 0  =
=  х0
х0  . Пусть теперь x0 = 0. Найдем приращение функции в этой точке:
. Пусть теперь x0 = 0. Найдем приращение функции в этой точке:
 ( h) = f(0+h) – f(0) = (0+h)
( h) = f(0+h) – f(0) = (0+h) 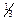 - 0
- 0 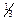 =h
=h 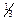 . Cледовательно,
. Cледовательно, 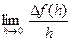 =
=  =
=  . Таким образом, разностное отношение не имеет конечного предела, поэтому
. Таким образом, разностное отношение не имеет конечного предела, поэтому  не существует.
не существует.
Пример 7. Пусть f(x) = |х| =  Найдем приращение функции в точке x0 = 0:
Найдем приращение функции в точке x0 = 0:  ( h) = f(0+h) – f(0) = |0+h| - |0| = |h|. Отсюда:
( h) = f(0+h) – f(0) = |0+h| - |0| = |h|. Отсюда:
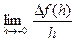 =
=  = 1 ;
= 1 ; 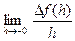 =
=  = -1. Односторонние пределы различны, поэтому
= -1. Односторонние пределы различны, поэтому 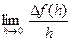 не существует, т.е.
не существует, т.е.  не существует.
не существует.
1.2. Функции, дифференцируемые в точке
Определение. Функцию 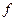 называют дифференцируемой в точке х0 , х0
называют дифференцируемой в точке х0 , х0 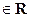 , если
, если
1) 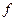 определена в некоторой окрестности
определена в некоторой окрестности  этой точки и
этой точки и
2) существует число А такое, что для приращения  ( h) функции
( h) функции 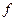 в точке
в точке
х0 справедлива асимптотическия формула:
 ( h) = Аh + o(h). (1)
( h) = Аh + o(h). (1)
Так как  ( h) = f(x0+h) – f(x0), то из (1) следует:
( h) = f(x0+h) – f(x0), то из (1) следует:
f(x0+h) = f(x0) + Аh + o(h) (2) Пусть х – произвольная точка из окрестности  ; положим h = x – x0 . Тогда x = x0 + +h и из (2) имеем:
; положим h = x – x0 . Тогда x = x0 + +h и из (2) имеем:
f(x) = f(x0) + А( x – x0) + o(x – x0) = А x+B+ o(x – x0), где B = f(x0) - А x0. Таким образом, для функции f в окрестности  справедливо асимптотическое представление f(x) = А x+B+ o(x – x0), где А и В – некоторые числа. В общих чертах содержание этой формулы можно передать следующей фразой: в малой окрестности точки x0 функция f(x) “почти не отличается ” от функции l(x) = Ax+B. Это свойство дифференцируемой функции используется для упрощения решений мно- гих задач математического анализа, ибо позволяет заменить функцию f(x), которая может быть весьма сложным обьектом, функцией простейшей структуры l(x) = Ax+B.
справедливо асимптотическое представление f(x) = А x+B+ o(x – x0), где А и В – некоторые числа. В общих чертах содержание этой формулы можно передать следующей фразой: в малой окрестности точки x0 функция f(x) “почти не отличается ” от функции l(x) = Ax+B. Это свойство дифференцируемой функции используется для упрощения решений мно- гих задач математического анализа, ибо позволяет заменить функцию f(x), которая может быть весьма сложным обьектом, функцией простейшей структуры l(x) = Ax+B.
Теорема 1. (Критерий дифференцируемости) Для того, чтобы функция f была дифференцируемой в точке х0 , х0 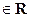 , необходимо и достаточно, чтобы существовала производная
, необходимо и достаточно, чтобы существовала производная  .
.
► Необходимость. Пусть справедливо представление (1) . Тогда
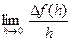 =
=  =
= 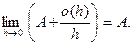
Таким образом,  существует и равна А.
существует и равна А.
Достаточность. Пусть существует 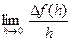 =
=  . Для h, достаточно малых по модулю, т.е. для
. Для h, достаточно малых по модулю, т.е. для  определим функцию α(h ) :
определим функцию α(h ) :

Тогда для всех h 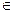
 можем записать равенство
можем записать равенство  ( h) =
( h) =  h + h α (h). Так как
h + h α (h). Так как 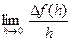 =
=  , то α(h )→ 0 при h→ 0. Отсюда:
, то α(h )→ 0 при h→ 0. Отсюда: 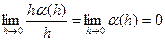 , т.е. h α (h) = o(h). Итак, для
, т.е. h α (h) = o(h). Итак, для  ( h) справедливо представление (1), в котором А =
( h) справедливо представление (1), в котором А =  , поэтому
, поэтому 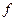 дифференцируема в точке х0 . ◄
дифференцируема в точке х0 . ◄
Следствие 1. Если функция 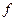 дифференцируема в точке х0 , то константа А в формуле (1) определяется единственным образом, а именно, А =
дифференцируема в точке х0 , то константа А в формуле (1) определяется единственным образом, а именно, А =  .
.
Это равенство получено при доказательстве необходимости.
Следствие 2. Для приращения функции, дифференцируемой в точке х0 , при всех h, достаточно малых по модулю имеет место представление
 ( h) =
( h) =  h + h α (h) , (3) где α (h) – некоторая функция, удовлетворяющая требованиям: α(h )→ 0 при h→ 0 и α(0 )= 0.
h + h α (h) , (3) где α (h) – некоторая функция, удовлетворяющая требованиям: α(h )→ 0 при h→ 0 и α(0 )= 0.
Равенство (3) получено при доказательстве достаточности.
Функции, рассмотренные в примерах 2,3 и 4 имеют производные в каждой точке х0 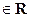 ; в силу теоремы 1 эти функции дифференцируемы во всех точках числовой оси. Степенная функция f(x) =х
; в силу теоремы 1 эти функции дифференцируемы во всех точках числовой оси. Степенная функция f(x) =х  , где μ – некоторое вещественное число, дифференцируема во всех точках х0
, где μ – некоторое вещественное число, дифференцируема во всех точках х0 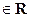 , х0≠0, в кото- рых она определена (см. пример 5 и замечание к нему). Функции f(x) = х
, х0≠0, в кото- рых она определена (см. пример 5 и замечание к нему). Функции f(x) = х 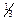 и f(x) = |х| не имеют производных в точке х0 = 0, значит, они не являяются дифференцируемыми в этой точке ( см. примеры 5 и 7).
и f(x) = |х| не имеют производных в точке х0 = 0, значит, они не являяются дифференцируемыми в этой точке ( см. примеры 5 и 7).
Теорема 2.(О непрерывности дифференцируемой функции)
Если функция дифференцируема в точке, то она и непрерывна в ней.
► Пусть функция f дифференцируема в точке х0. Тогда справедливо представление (1), из которого следует:  ( h) → 0 при h→ 0 . В силу теоремы о приращении непрерывной функции (гл. 1, п. 5.1) функция f непрерывна в точке х0 .◄
( h) → 0 при h→ 0 . В силу теоремы о приращении непрерывной функции (гл. 1, п. 5.1) функция f непрерывна в точке х0 .◄
Замечание. Согласно теореме 2 из дифференцируемости функции вытекает ее непрерывность. Обратное утверждение неверно: функция, непрерывная в точке, может оказаться не дифференцируемой в этой точке. Например, f(x) = |х| непрерывна в точке х0 = 0, но не дифференцируема в ней (см. пример 7).
1.3. Теоремы, облегчающие вычисление производных
Теорема 3.(Об арифметических действиях с дифференцируемыми функциями) Пусть функции f и g дифференцируемы в точке х0. Тогда:
1. функция F =f+g дифференцируемa в точке х0 , причем
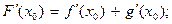
2. функция F =f g дифференцируемa в точке х0 , причем
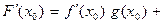
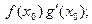
3. если 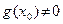 , то функция F =
, то функция F =  дифференцируемa в точке х0 ,
дифференцируемa в точке х0 ,
причем  .
.
► Так как f и g дифференцируемы в точке х0 , то справедливы асимптотические формулы ( см. (2) ):
f(x0+h) = f(x0) +  h + o(h) ;
h + o(h) ;
g(x0+h) = g(x0) + 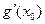 h + o(h). (4)
h + o(h). (4)
1. Пусть F =f+g . Воспользовавшись формулами (4), получим:
 Для приращения
Для приращения 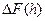 мы получили представление
мы получили представление 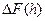 = Аh + o(h), в котором А =
= Аh + o(h), в котором А =  . Значит, F дифференцируема в точке х0 , причем
. Значит, F дифференцируема в точке х0 , причем  =
= 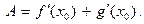
2. Пусть F =f g. Воспользовавшись (4), получим:
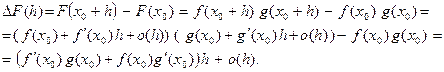 Для приращения
Для приращения 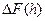 получено представление
получено представление 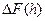 = Аh + o(h), в котором А =
= Аh + o(h), в котором А =  +
+ 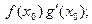 Значит, F дифференцируема в точке х0 , причем
Значит, F дифференцируема в точке х0 , причем 
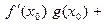
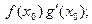
3. Пусть 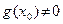 , а F =
, а F =  . Функция g дифференцируема, и потому она непрерывна в точке х0 . В силу теоремы о сохранении знака непрерывной функции ( гл.1. п.5.1) существует окрестность
. Функция g дифференцируема, и потому она непрерывна в точке х0 . В силу теоремы о сохранении знака непрерывной функции ( гл.1. п.5.1) существует окрестность  такая, что для любого х из этой окрестности
такая, что для любого х из этой окрестности  . Следовательно, функция F определена в
. Следовательно, функция F определена в  . Обозначим:
. Обозначим:
А =  , и покажем, что справедливо представление
, и покажем, что справедливо представление 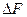 ( h) = Аh + o(h). Имеем:
( h) = Аh + o(h). Имеем:
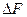 ( h) =
( h) =  Воспользовавшисьформулами (4), в числителе последней дроби получим:
Воспользовавшисьформулами (4), в числителе последней дроби получим:
 Отсюда:
Отсюда:
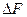 ( h) =
( h) = 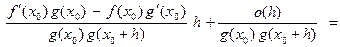
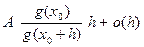 .
.
Обозначим: α(h) = 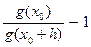 . Очевидно, α(h )→ 0 при h→ 0 и
. Очевидно, α(h )→ 0 при h→ 0 и  α(h). Теперь можем записать:
α(h). Теперь можем записать:
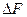 ( h) = А (1 + α(h)) h + o(h) = Ah + Аhα(h) + o(h)). Но Аα(h) h = o(h) и o(h)+ o(h)= o(h) , поэтому
( h) = А (1 + α(h)) h + o(h) = Ah + Аhα(h) + o(h)). Но Аα(h) h = o(h) и o(h)+ o(h)= o(h) , поэтому 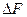 ( h) = Ah +o(h).
( h) = Ah +o(h).
Значит, F дифференцируема и  А =
А =  . ◄
. ◄
Пример 8. Пусть f(x)= sinx, g(x) = cosx, F(x) = 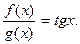 Воспользовавшись утверждением 3) доказанной теоремы, для всякого х0 , х0 ≠
Воспользовавшись утверждением 3) доказанной теоремы, для всякого х0 , х0 ≠  , где n – любое целое число, получим:
, где n – любое целое число, получим:
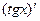 =
= 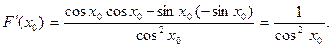 Аналогичные выкладки в случае F(x) =
Аналогичные выкладки в случае F(x) =  и х0 , х0 ≠
и х0 , х0 ≠ 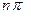 , где n – любое целое число, дадут:
, где n – любое целое число, дадут: 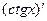 =
= 
Теорема4. ( О производной сложной функции) Пусть функция f дифференцируема в точке х0 , а функция g дифференцируема в точке у0 , где у0 = f(x0). Тогда сложная функция  дифференцируема в точке х0 , причем.
дифференцируема в точке х0 , причем. 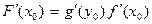 .
.
► Функции f и g дифференцируемы , а потому и непрерывны в точках х0 и у0 . По теореме о непрерывности сложной функции (гл. 1, п.5.2)  определена в некоторой окрестности
определена в некоторой окрестности  и непрерывна в точке х0.
и непрерывна в точке х0.
Пусть h достаточно мало по модулю, так что х0+ h 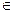
 . Обозначим:
. Обозначим:
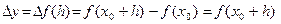
 . Тогда f(x0+h) = y0 +
. Тогда f(x0+h) = y0 + 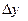 ; поэтому
; поэтому  т.е.
т.е. 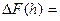
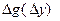 .
.
В силу формулы (3)  , где α(Δу) – некоторая функция такая, что α(Δу) → 0 при Δу → 0 и α(0) = 0. Так как f дифференцируема, то
, где α(Δу) – некоторая функция такая, что α(Δу) → 0 при Δу → 0 и α(0) = 0. Так как f дифференцируема, то 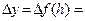
 h + o(h). Подставляя эти выражения для
h + o(h). Подставляя эти выражения для 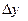 , получим:
, получим:
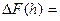
 =
=
= 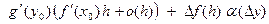 =
= 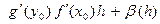 , где
, где  . Покажем, что
. Покажем, что  . Имеем:
. Имеем:
 . Заметим:
. Заметим: 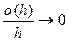 ,
,  при
при  . Кроме того,
. Кроме того, 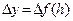 - приращение непрерывной функции, поэтому
- приращение непрерывной функции, поэтому 
 при
при  . Так как α(Δу) → 0 при Δу → 0 (см. выше), а
. Так как α(Δу) → 0 при Δу → 0 (см. выше), а 
 при
при  , то α(Δу) → 0 при
, то α(Δу) → 0 при  . Таким образом, оба слагаемые в правой части написанного выше равенства стремятся к нулю при
. Таким образом, оба слагаемые в правой части написанного выше равенства стремятся к нулю при  ; следовательно,
; следовательно, 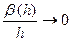 при
при  , т.е.
, т.е.  .
.
Итак, 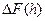 = Аh + o(h), где А =
= Аh + o(h), где А = 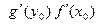 , из чего вытекает и дифференцируемость
, из чего вытекает и дифференцируемость  , и равенство
, и равенство 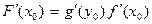 . ◄
. ◄
Теорема 5. (О производной обратной функции)Пусть функция f непрерывна и строго монотонна в окрестности  ,
, 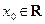 . Если f дифференцируема в точке х0, а
. Если f дифференцируема в точке х0, а 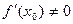 , то обратная функция
, то обратная функция  дифференцируема в точке у0 , у0 = f(х0), причем
дифференцируема в точке у0 , у0 = f(х0), причем  .
.
► По теореме о непрерывности обратной функции (гл. 1, п.5.5) обратная функция  непрерывна на некотором интервале (с, d), содержащем точку у0 = f(х0) и строго монотонна на нем. Пусть
непрерывна на некотором интервале (с, d), содержащем точку у0 = f(х0) и строго монотонна на нем. Пусть  отлично от нуля и достаточно мало по модулю, так что у0 +
отлично от нуля и достаточно мало по модулю, так что у0 + 
 (с, d). Обозначим:
(с, d). Обозначим: 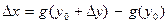 . Так как у0 = f(х0), а
. Так как у0 = f(х0), а  , то g(y0) =
, то g(y0) =  = x0 . Значит, g(y0+
= x0 . Значит, g(y0+  ) = g(y0) +
) = g(y0) +  = x0 +
= x0 +  . Из g(y0+
. Из g(y0+  ) = = x0 +
) = = x0 +  следует: y0+
следует: y0+  =f( x0 +
=f( x0 +  ),
),  = f( x0 +
= f( x0 +  ) – у0 = f( x0 +
) – у0 = f( x0 +  ) -- f(х0). Таким образом,
) -- f(х0). Таким образом, 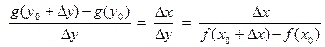 . Так как
. Так как  ≠ 0, а g – строго монотонная функция, то
≠ 0, а g – строго монотонная функция, то 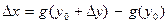 отлично от нуля, поэтому последнюю дробь можно перевернуть:
отлично от нуля, поэтому последнюю дробь можно перевернуть:
 . Перейдем в этом равенстве к пределу при
. Перейдем в этом равенстве к пределу при 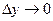 . Заметим,что при
. Заметим,что при 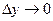 стремится к нулю и
стремится к нулю и  , ибо
, ибо  является приращением непрерывной функции
является приращением непрерывной функции  (см. выше). Заметим еще, что
(см. выше). Заметим еще, что  . Таким образом,
. Таким образом, 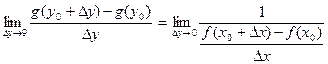 =
=  , т.е.
, т.е.  существует и равна
существует и равна 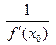 . ◄
. ◄
Пример 9. Пусть f(x) = a 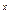 , где a> 0, a ≠ 1. Эта функция непрерывна и строго монотонна на всей числовой оси, причем (см. пример 2) при вся- ком
, где a> 0, a ≠ 1. Эта функция непрерывна и строго монотонна на всей числовой оси, причем (см. пример 2) при вся- ком 

 . В силу доказанной теоремы обратная функ- ция
. В силу доказанной теоремы обратная функ- ция 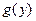
 дифференцируема в точке y0 = a
дифференцируема в точке y0 = a  , а
, а  .
. 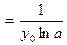 Так как здесь х0 – любое вещественное число, то у0 - любое положительное число.
Так как здесь х0 – любое вещественное число, то у0 - любое положительное число.
Пример 10. Пусть f(x) = sinx. Эта функция непрерывна и строго монотонна на 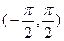 , и при любом
, и при любом  из этого интервала
из этого интервала  cos
cos 
 . Значит, обратная функция g(y) = arcsiny дифференцируема в точке y0 = = sinx0 , a
. Значит, обратная функция g(y) = arcsiny дифференцируема в точке y0 = = sinx0 , a  . Так как
. Так как  - любая точка интервала
- любая точка интервала 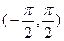 , то y0 - любое число из интервала (-1 ,1).
, то y0 - любое число из интервала (-1 ,1).
Пример 11. Пусть f(x) = tgx. Эта функция непрерывна и строго монотонна на 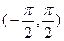 , и при любом
, и при любом  из этого интервала
из этого интервала 

 . Значит, обратная функция g(y) = arctgy дифференцируема в точке y0 = tgx0, a
. Значит, обратная функция g(y) = arctgy дифференцируема в точке y0 = tgx0, a 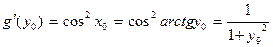 . Так как
. Так как  - любая точка интервала
- любая точка интервала 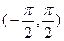 , то y0 - любое вещественное число.
, то y0 - любое вещественное число.
1.4. Дифференциал функции
Пусть функция f (х) определена в окрестности  = (α , β), α <
= (α , β), α <  < β, и дифференцируема в точке
< β, и дифференцируема в точке  . Приращение
. Приращение 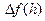 = f(x0 +h) – f(x0) функции в точке
= f(x0 +h) – f(x0) функции в точке  можно рассматривать как функцию от h, которая определена для тех h, при которых точка
можно рассматривать как функцию от h, которая определена для тех h, при которых точка  + h
+ h  (α , β) , т.е. для h
(α , β) , т.е. для h 
 = (α -
= (α -  , β -
, β -  ) ; h называют приращением аргумента х и обычно обозначают через Δх. Из формулы (1) следует, что функция
) ; h называют приращением аргумента х и обычно обозначают через Δх. Из формулы (1) следует, что функция 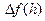 является бесконечно малой при
является бесконечно малой при  , причем, если А
, причем, если А  0, то порядок её равен единице, а произведение А h (напомним: А =
0, то порядок её равен единице, а произведение А h (напомним: А =  )есть её главная часть (гл. 1, п.) . Если же А = 0, то порядок бесконечно малой
)есть её главная часть (гл. 1, п.) . Если же А = 0, то порядок бесконечно малой 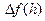 выше единицы.
выше единицы.
Определение. Дифференциалом функции f в точке  назовем произведение
назовем произведение  h, где h – переменная, принимающая значения в окрестности точки 0:
h, где h – переменная, принимающая значения в окрестности точки 0: 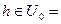
 .
.
Обозначать дифференциал будем символами df и df(h) :
df(h) 
 h. Из (1) следует: при h
h. Из (1) следует: при h 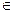
 = (α -
= (α -  , β -
, β -  )
)
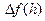 = df(h) + о(h) (5)
= df(h) + о(h) (5)
Если 
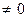 , то дифференциал df(h) представляет собой главную часть при- ращения
, то дифференциал df(h) представляет собой главную часть при- ращения 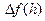 . Если же
. Если же 
 , то при любых h df(h) = 0, т.е. дифференциал в этом случае тождественно равен нулю. При h, малых по модулю дифференциал функции ”почти не отличается ” от её приращения (см. формулу (5)); это обстоятельство позволяет упрощать решения многих задач, заменяя приращение
, то при любых h df(h) = 0, т.е. дифференциал в этом случае тождественно равен нулю. При h, малых по модулю дифференциал функции ”почти не отличается ” от её приращения (см. формулу (5)); это обстоятельство позволяет упрощать решения многих задач, заменяя приращение 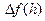 простым и удобным в обращении выражением – дифференциалом df(h). Так поступают, например, если требуется найти приближенное значение функции в заданной точке.
простым и удобным в обращении выражением – дифференциалом df(h). Так поступают, например, если требуется найти приближенное значение функции в заданной точке.
Пример 12. Найдем приближенно значеиие  . Положим f(x)= =
. Положим f(x)= =  , х0 =8, h = 0,12. Тогда
, х0 =8, h = 0,12. Тогда  = f(x0+h), f(x0) =2. Заметим:
= f(x0+h), f(x0) =2. Заметим:  ( h) = f(x0+h) – f(x0); f(x0+h) = = f(x0) +
( h) = f(x0+h) – f(x0); f(x0+h) = = f(x0) +  ( h) ≈
( h) ≈  f(x0) + df(h). Отсюда, положив h = 0,12, получим:
f(x0) + df(h). Отсюда, положив h = 0,12, получим:  ≈ 2 + + df (0,12) . Вычислим значение дифференциала df(h) в точке х0 =8 при h = 0,12. Имеем:
≈ 2 + + df (0,12) . Вычислим значение дифференциала df(h) в точке х0 =8 при h = 0,12. Имеем: 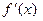 =
=  ,
,  =
= 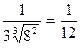 , значит, df(h)=
, значит, df(h)=  h =
h =  h =.
h =.  0,12 Теперь найдем:
0,12 Теперь найдем:  ≈ 2 + df(0,12) = 2 +
≈ 2 + df(0,12) = 2 +  0,12 = 2 + 0,01 = 2,01.
0,12 = 2 + 0,01 = 2,01.
