А. Сложение колебаний одинаковой частоты, происходящих вдоль одной прямой

Колебания и волны

Предисловие

Для лучшего понимания этого материала нужно знать раздел математики «комплексные числа».

План

1. Колебательные процессы. Гармонические колебания. Понятие о спектральном разложении.

2. Дифференциальное уравнение гармонических колебаний.

3. Пружинный, физический и математический маятники.

4. Энергия гармонического осциллятора.

5. Сложение колебаний.

5а. Сложение колебаний одинаковой частоты, происходящих вдоль одной прямой.

5b. Сложение взаимно перпендикулярных колебаний одинаковой частоты.

5с. Сложение взаимно перпендикулярных колебаний кратных частот. Фигуры Лиссажу.

6. Затухающие колебания.

7. Вынужденные колебания.

8. Упругие волны. Основные понятия.

9. Дифференциальное уравнение волны.

10. Стоячие волны.

11. Скорость упругих волн.

12. Энергия волны. Групповая скорость. Вектор плотности потока энергии (вектор Умова). Интенсивность волны.

13. Элементы акустики.

14. Эффект Доплера для звуковых волн.

1. Колебательные процессы. Гармонические колебания. Понятие о спектральном разложении

Любой процесс, повторяющийся во времени, является колебательным. Физическая природа колебаний может быть различна: может изменяться координата (механические колебания), сила тока, напряжённость электрического или магнитного поля (электромагнитные колебания) и т.д., но физически различные процессы описываются одинаковыми уравнениями.

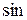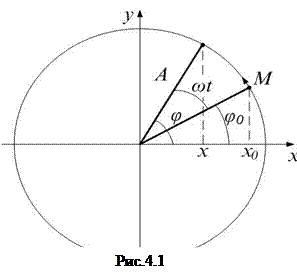
Рассмотрим гармонические колебания, то есть колебания, происходящие по гармоническому закону ( или 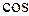). Представим себе материальную точку М, равномерно вращающуюся по окружности радиуса А с угловой скоростью ω (рис.4.1). Тогда проекция точки М на ось х будет совершать периодические колебания вдоль оси OX:

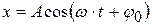, (4.1)

где А – амплитуда колебаний (абсолютное значение максимального смещения), 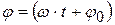– фаза колебаний, которая определяет угловое смещение точки М в любой момент времени, 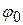– начальная фаза, 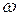– круговая (циклическая) частота, равная

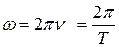; (4.2)

ν – частота колебаний (число полных колебаний в единицу времени, 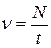, 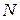– число колебаний за время t), 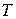– период колебаний (время совершения одного полного колебания). Выражение (4.1) – кинематическое уравнение гармонического колебательного движения.

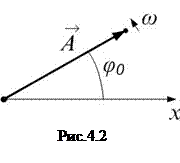Можно представить гармонические колебания графически – это метод векторных диаграмм. Вращение вектора 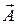на рис.4.2 эквивалентно гармоническому колебанию.

Ещё одно возможное представление гармонических колебаний – представление в виде комплексного числа:

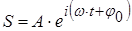. (4.3)

При этом не теряется информация о координате y точки М на рис.4.1, поскольку из (4.3) по формуле Эйлера получим:

,

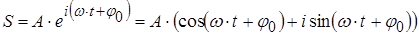или

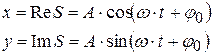
Ещё одно преимущество записи колебания (4.3): физические задачи на колебания сводятся просто к операциям с комплексными числами.

Почему рассматриваем в первую очередь именно гармонические колебания? Ведь реальные процессы чаще описываются негармоническими функциями. По теореме Фурье любую периодическую функцию 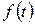с периодом 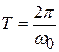( 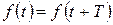) можно представить в виде ряда (ряд Фурье):

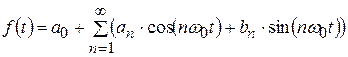, (4.4)

где

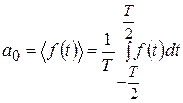– среднее значение функции ;

; .

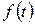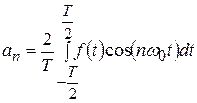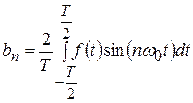Иными словами, любое периодическое колебание можно представить в виде суперпозиции гармонических колебаний кратных частот 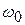, , 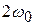, 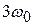…. Частота 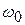называется основной частотой; – первый обертон и т.д.

Определение: совокупность частот и соответствующих им амплитуд называется спектром колебания. Спектр можно представить графически. Пусть – чётная:

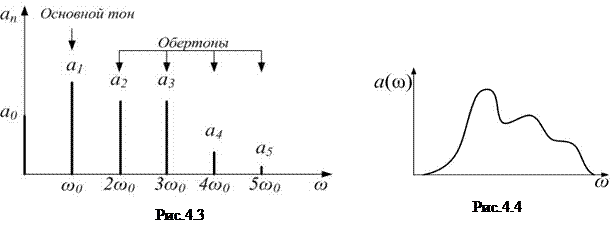
тогда все 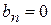: 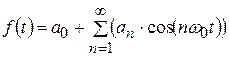, и спектр состоит только из чётных гармоник (рис.4.3).

Реально можно ограничиться первыми несколькими членами ряда, если функция не очень «плохая».

Периодическая функция имеет дискретный спектр. Непериодическую тоже можно разложить по гармоническим составляющим, но это она будет иметь непрерывный спектр 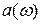(рис.4.4), а ряд Фурье переходит в интеграл Фурье.

2. Дифференциальное уравнение гармонических колебаний.

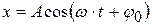, (4.1)

Скорость 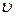колеблющейся материальной точки получим, продифференцировав (4.1) по времени:

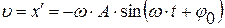. (4.5)

Продифференцировав (4.5), получим ускорение а:

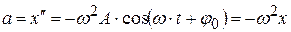. (4.6)

Или:

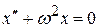. (4.7)

Выражение (4.7) описывает гармонические колебания величины x и называется дифференциальным уравнением гармонического осциллятора. Его решением является гармоническая функция (4.1). Если вторая производная по времени какой-либо физической величины (не обязательно смещения) пропорциональна самой величине с противоположным знаком, то данная физическая величина изменяется со временем по гармоническому закону.

3. Пружинный, физический и математический маятники

По второму закону Ньютона найдём из (4.6) силу, действующую на колеблющееся тело:

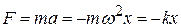, (4.8)

где принято обозначение

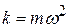. (4.9)

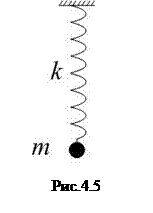Сила пропорциональна смещению из положения равновесия и противоположна ему; её называют возвращающей (направлена к положению равновесия), или квазиупругой (описывается формально так же, как и упругая сила по закону Гука). Для пружинного маятника (рис.4.5) коэффициент пропорциональности 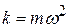имеет смысл жёсткости пружины. Круговая частота и период колебаний такого маятника:

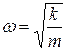; (4.10)

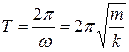. (4.11)

Физическим маятником называется твёрдое тело, способное колебаться в поле силы тяжести относительно оси, не проходящей через центр масс (рис.4.6).

Длина физического маятника 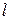– это расстояние между центром масс С и осью вращения (точка О). Плечо силы тяжести равно

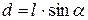, (4.12)

где 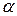– угол отклонения из положения равновесия. Момент силы тяжести относительно оси вращения

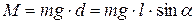; (4.13)

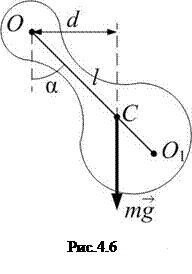для малых углов отклонения

,

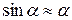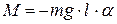. (4.14)

Знак «–» в (4.14) поставили потому, что проекция углового перемещения на ось вращения противоположна по знаку проекции момента силы. По закону динамики для вращательного движения (3.13) 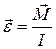, где 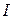– момент инерции маятника относительно оси вращения тогда угловое ускорение

,

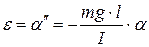или

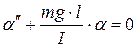. (4.15)

Уравнение (4.15) – это дифференциальное уравнение гармонических колебаний типа (4.7), где роль переменной величины играет угол отклонения маятника:

,

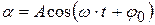а коэффициент при 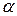– квадрат круговой частоты:

.

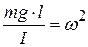Период колебаний физического маятника

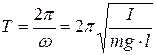. (4.16)

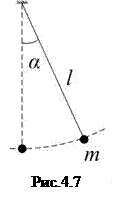Частным случаем физического маятника является маятник математический: материальная точка (тело, размерами которого можно пренебречь), подвешенная на нерастяжимой невесомой нити (рис.4.7). Для материальной точки момент инерции 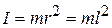; тогда

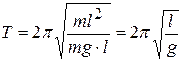. (4.17)

Введём определение для физического маятника: приведённая длина физического маятника – это длина такого математического маятника, который имеет тот же период колебаний. По определению

,

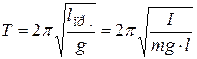откуда

.

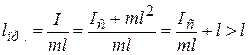Здесь 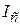– момент инерции тела относительно оси, проходящей через центр масс; 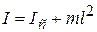– по теореме Штейнера. Приведённая длина физического маятника 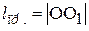(рис.4.6) всегда больше его длины 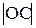; в частном случае математического маятника они совпадают. Точка 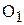называется точкой качаний; она с точкой подвеса О обладает свойством взаимности: если маятник перевернуть и подвесить за 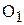, период колебаний будет таким же.

4. Энергия гармонического осциллятора.

Поскольку смещение из положения равновесия и скорость колеблющейся точки равны соответственно

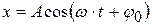, (4.1)

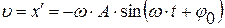, (4.5)

то полная энергия осциллятора, равная сумме кинетической и потенциальной:

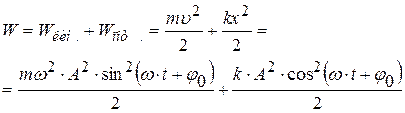
Поскольку

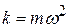, (4.9)

то

.

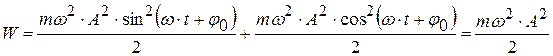Итак, полная энергия гармонического осциллятора не изменяется и равна:

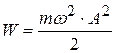. (4.18)

Энергия лишь преобразуется из кинетической в потенциальную и обратно. Максимальные значения кинетической и потенциальной равны

,

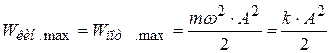а средние

.

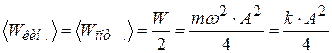а. Сложение колебаний одинаковой частоты, происходящих вдоль одной прямой.

Пусть точка одновременно участвует в двух колебаниях одинаковой частоты:

,

,

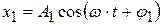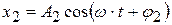тогда результирующее смещение точки из положения равновесия тоже будет гармоническим колебанием с той же частотой:

.

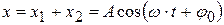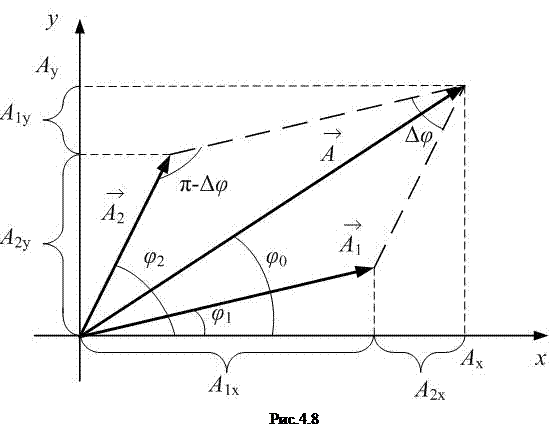Найдём амплитуду и начальную фазу этого колебания по методу векторных диаграмм (рис. 4.8).

;

; ;

;

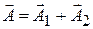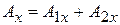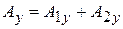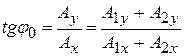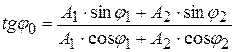; (4.19)

,

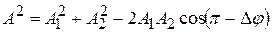где ;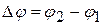

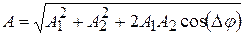. (4.20)

При сложении не двух, а большего числа колебаний одинаковой частоты

,

,

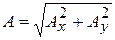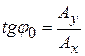где ; .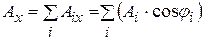

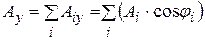Частные случаи: 1) если сдвиг фаз колебаний 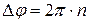, где n – целое число (колебания происходят в одной фазе), то 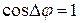, и колебания усиливают друг друга: 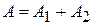(см.4.20);

2) если 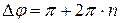, то 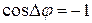, 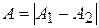- колебания происходят в противофазе и ослабляют друг друга; а в случае 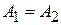получим .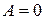