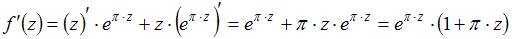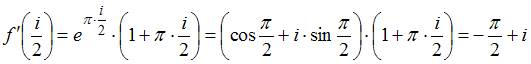Тема: Операции над комплексными числами
Произведение комплексных чисел 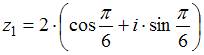 и
и 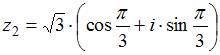 равно
равно 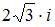
Решение: Произведение двух комплексных чисел, заданных в тригонометрической форме,
находится по формуле: 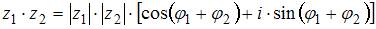 В нашем случае получим
В нашем случае получим 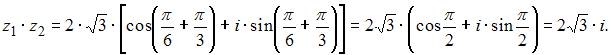
Тема: Дифференцирование функции комплексного переменного
Если 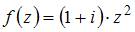 , то
, то 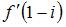 равно 4.
равно 4.
Решение:
Производная функции 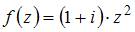 равна
равна 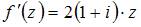 тогда
тогда 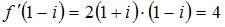
Тема: Особые точки функции комплексного переменного
Для функции 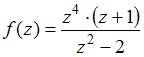 точка
точка 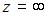 является
является
полюсом третьего порядка
Решение:
Порядок полюса функции вида 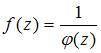 равен порядку нуля
равен порядку нуля 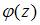 . Т.к.
. Т.к. 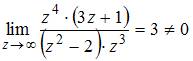 то точка
то точка 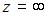 является полюсом третьего порядка.
является полюсом третьего порядка.
Тема: Операции над комплексными числами
Сумма комплексных чисел 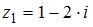 и
и 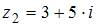 равна
равна 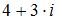
Тема: Области на комплексной плоскости
Все точки 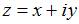 комплексной плоскости, принадлежащие множеству
комплексной плоскости, принадлежащие множеству 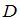 , изображенному на рисунке:
, изображенному на рисунке:
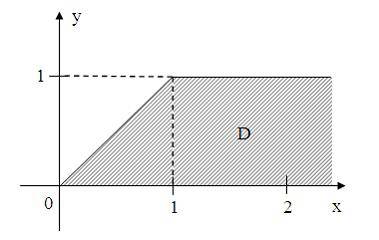
удовлетворяют условию … 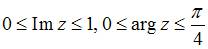
Решение:
Множество 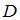 , изображенное на рисунке, ограничено прямыми
, изображенное на рисунке, ограничено прямыми 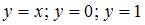 Для комплексного числа
Для комплексного числа 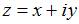 :
: 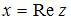 – действительная часть
– действительная часть 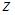 ,
, 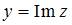 - мнимая часть, угол наклона прямой
- мнимая часть, угол наклона прямой 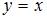 к оси х равен
к оси х равен 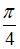 . Следовательно, комплексные числа
. Следовательно, комплексные числа 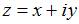 должны удовлетворять условиям
должны удовлетворять условиям 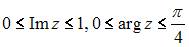 .
.
Тема: Операции над комплексными числами
Частное 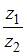 комплексных чисел
комплексных чисел 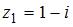 и
и 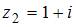 равно …
равно … 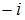
Решение:
Частное двух комплексных чисел находится по формуле 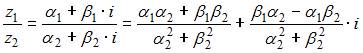 .
.
В нашем случае получим 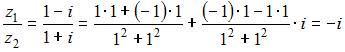
Тема: Особые точки функции комплексного переменного
Для функции 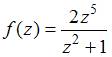 точка
точка 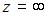 является …
является …
 | полюсом третьего порядка |
Решение:
Порядок полюса функции вида 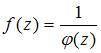 равен порядку нуля
равен порядку нуля 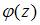 .
.
Так как 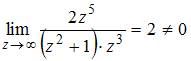 , то точка
, то точка 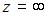 будет полюсом третьего порядка.
будет полюсом третьего порядка.
Тема: Области на комплексной плоскости
Все точки 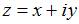 комплексной плоскости, принадлежащие множеству
комплексной плоскости, принадлежащие множеству 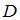 , изображенному на рисунке:
, изображенному на рисунке:
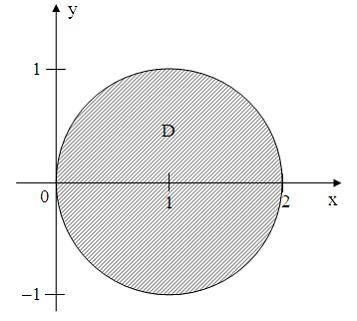
удовлетворяют условию …
 | 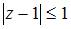 | ||
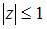 | |||
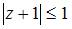 | |||
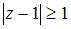 |
Решение:
Множество 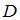 , изображенное на рисунке, представляет собой круг с центром в точке
, изображенное на рисунке, представляет собой круг с центром в точке 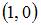 и радиусом
и радиусом 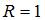 . Уравнение окружности радиуса
. Уравнение окружности радиуса 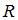 с центром в точке
с центром в точке 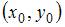 имеет вид:
имеет вид: 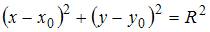 . Следовательно, все точки, принадлежащие множеству
. Следовательно, все точки, принадлежащие множеству 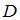 , удовлетворяют неравенству
, удовлетворяют неравенству 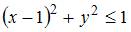 , или
, или 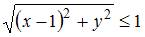 . Модуль комплексного числа
. Модуль комплексного числа 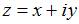 равен
равен 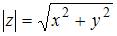 . Тогда модуль комплексного числа
. Тогда модуль комплексного числа 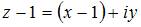 равен
равен 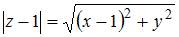 . Следовательно, точки комплексной плоскости, принадлежащие множеству
. Следовательно, точки комплексной плоскости, принадлежащие множеству 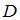 , удовлетворяют условию
, удовлетворяют условию 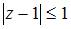 .
.
Тема: Дифференцирование функции комплексного переменного
Если 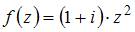 , то
, то 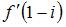 равно …
равно …
 | |||
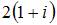 | |||
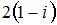 |
Решение:
Производная функции 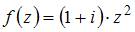 равна
равна 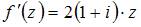 .
.
Тогда 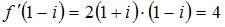
Тема: Дифференцирование функции комплексного переменного
Значение производной функции 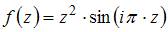 в точке
в точке 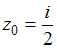 равно …
равно …
 | 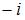 | ||
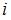 | |||
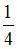 | |||
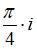 |
Решение:
Производная функции 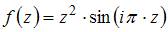 имеет вид
имеет вид 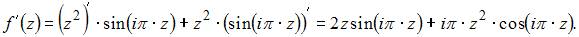 . Тогда
. Тогда 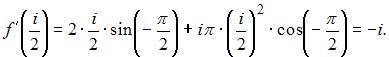
Тема: Операции над комплексными числами
Произведение комплексных чисел
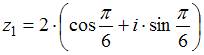 и
и 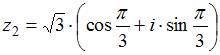 равно
равно 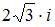
Тема: Области на комплексной плоскости
Все точки 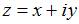 комплексной плоскости, принадлежащие множеству
комплексной плоскости, принадлежащие множеству 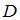 , изображенному на рисунке:
, изображенному на рисунке:
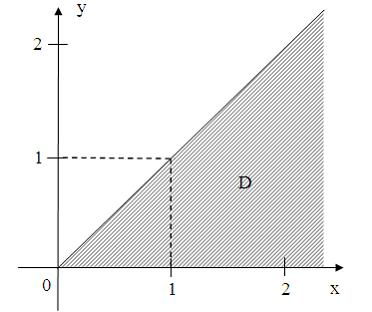
удовлетворяют условию …
 | 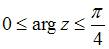 | ||
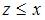 | |||
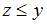 | |||
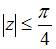 |
Решение:
Множество 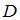 , изображенное на рисунке, ограничено прямыми
, изображенное на рисунке, ограничено прямыми 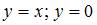 .
.
Для комплексного числа 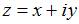 угол наклона прямой
угол наклона прямой 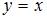 к оси
к оси 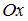 равен
равен 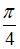 . Следовательно, комплексные числа
. Следовательно, комплексные числа 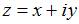 , принадлежащие множеству
, принадлежащие множеству 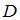 , должны удовлетворять условиям
, должны удовлетворять условиям 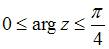
Тема: Дифференцирование функции комплексного переменного
Если 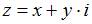 и
и 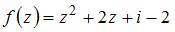 , то мнимая часть производной этой функции
, то мнимая часть производной этой функции 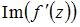 имеет вид …
имеет вид …
 | 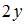 | ||
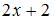 | |||
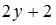 | |||
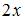 |
Решение:
Производная функции 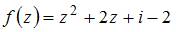 равна
равна 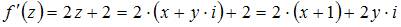 .
.
Тогда 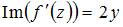
Тема: Операции над комплексными числами
Дано комплексное число 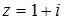 . Тогда
. Тогда 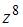 равно 16
равно 16
Тема: Дифференцирование функции комплексного переменного
Значение производной функции 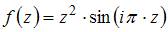 в точке
в точке 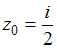 равно …
равно …
 | 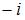 | ||
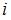 | |||
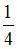 | |||
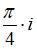 |
Решение:
Производная функции 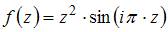 имеет вид
имеет вид 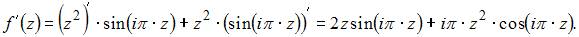
Тогда
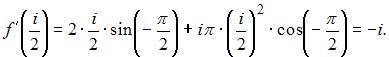
Тема: Области на комплексной плоскости
Все точки 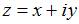 комплексной плоскости, принадлежащие множеству
комплексной плоскости, принадлежащие множеству 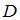 , изображенному на рисунке:
, изображенному на рисунке:
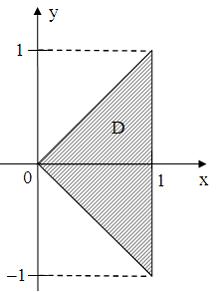
удовлетворяют условию …
 | 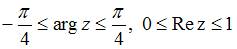 | ||
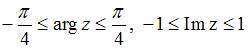 | |||
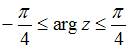 | |||
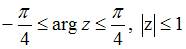 |
Решение:
Множество 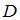 , изображенное на рисунке, ограничено прямыми
, изображенное на рисунке, ограничено прямыми 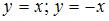 и
и 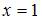 . Для комплексного числа
. Для комплексного числа 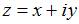 угол наклона прямой
угол наклона прямой 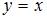 к оси
к оси 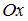 равен
равен 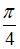 , а прямой
, а прямой 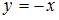 , равен
, равен 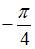 . Следовательно, комплексные числа
. Следовательно, комплексные числа 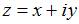 , принадлежащие множеству
, принадлежащие множеству 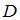 , должны удовлетворять условиям
, должны удовлетворять условиям 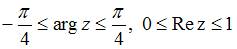 .
.
Тема: Операции над комплексными числами
Сумма комплексных чисел 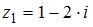 и
и 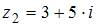 равна …
равна …
 | 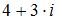 | ||
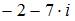 | |||
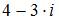 |
Решение:
Чтобы сложить два комплексных числа 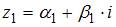 и
и 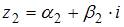 , надо сложить их вещественные и мнимые части, то есть
, надо сложить их вещественные и мнимые части, то есть 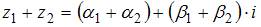 .
.
В нашем случае получим 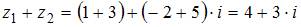 .
.
Тема: Особые точки функции комплексного переменного
Для функции 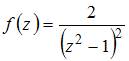 точка
точка 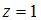 является …
является …
 | полюсом второго порядка | ||
| полюсом третьего порядка | |||
| полюсом первого порядка | |||
| существенно особой точкой |
Решение:
Порядок полюса функции вида 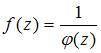 равен порядку нуля
равен порядку нуля 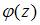 .
.
Имеем 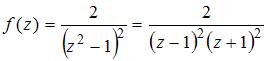 ,
,
поэтому точка 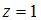 будет полюсом второго порядка.
будет полюсом второго порядка.
Тема: Области на комплексной плоскости
Все точки 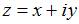 комплексной плоскости, принадлежащие множеству
комплексной плоскости, принадлежащие множеству 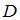 , изображенному на рисунке,
, изображенному на рисунке,
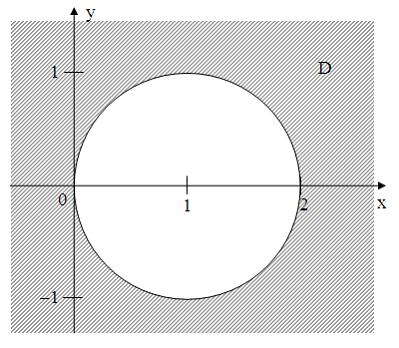
удовлетворяют условию …
 | 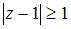 | ||
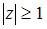 | |||
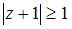 | |||
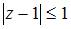 |
Тема: Особые точки функции комплексного переменного
Для функции 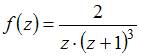 точка
точка 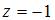 является …
является …
 | полюсом третьего порядка | ||
| полюсом второго порядка | |||
| полюсом первого порядка | |||
| существенно особой точкой |
Решение:
Порядок полюса функции вида 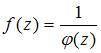 равен порядку нуля
равен порядку нуля 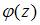 .
.
Имеем 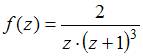 ,
,
поэтому точка 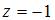 будет полюсом третьего порядка.
будет полюсом третьего порядка.
Тема: Операции над комплексными числами
Произведение комплексных чисел 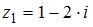 и
и 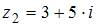 равно …
равно … 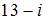
Тема: Дифференцирование функции комплексного переменного
Если 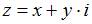 и
и 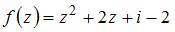 , то мнимая часть производной этой функции
, то мнимая часть производной этой функции 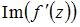 имеет вид …
имеет вид …
 | 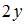 | ||
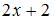 | |||
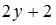 | |||
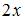 |
Тема: Операции над комплексными числами
Значение выражения 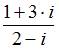 равно …
равно …
 | 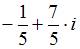 | ||
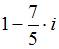 | |||
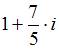 | |||
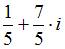 |
Тема: Области на комплексной плоскости
Все точки 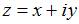 комплексной плоскости, принадлежащие множеству
комплексной плоскости, принадлежащие множеству 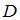 , изображенному на рисунке:
, изображенному на рисунке:

удовлетворяют условию …
 | 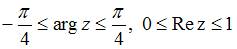 | ||
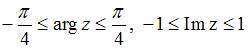 | |||
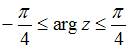 | |||
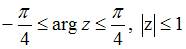 |
Решение:
Множество 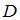 , изображенное на рисунке, ограничено прямыми
, изображенное на рисунке, ограничено прямыми 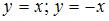 и
и 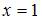 . Для комплексного числа
. Для комплексного числа 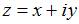 угол наклона прямой
угол наклона прямой 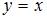 к оси
к оси 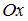 равен
равен 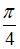 , а прямой
, а прямой 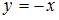 , равен
, равен 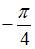 . Следовательно, комплексные числа
. Следовательно, комплексные числа 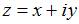 , принадлежащие множеству
, принадлежащие множеству 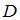 , должны удовлетворять условиям
, должны удовлетворять условиям 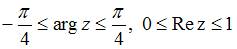 .
.
Тема: Особые точки функции комплексного переменного
Для функции 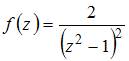 точка
точка 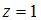 является …
является …
 | полюсом второго порядка | ||
| полюсом третьего порядка | |||
| полюсом первого порядка | |||
| существенно особой точкой |
Решение:
Порядок полюса функции вида 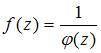 равен порядку нуля
равен порядку нуля 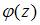 .
.
Имеем 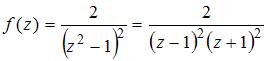 ,
,
поэтому точка 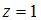 будет полюсом второго порядка.
будет полюсом второго порядка.
Тема: Дифференцирование функции комплексного переменного
Если 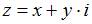 и
и 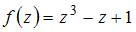 , то действительная часть производной этой функции
, то действительная часть производной этой функции 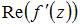 имеет вид …
имеет вид …
 | 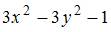 |
Тема: Особые точки функции комплексного переменного
Для функции 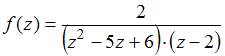 точка
точка 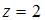 является …
является …
 | полюсом второго порядка | ||
| полюсом третьего порядка | |||
| полюсом первого порядка | |||
| существенно особой точкой |
Решение:
Порядок полюса функции вида 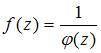 равен порядку нуля
равен порядку нуля 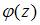 .
.
Так как 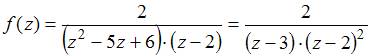 , то точка
, то точка 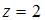 будет полюсом второго порядка.
будет полюсом второго порядка.
Тема: Области на комплексной плоскости
Все точки 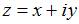 комплексной плоскости, принадлежащие множеству
комплексной плоскости, принадлежащие множеству 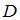 , изображенному на рисунке,
, изображенному на рисунке,
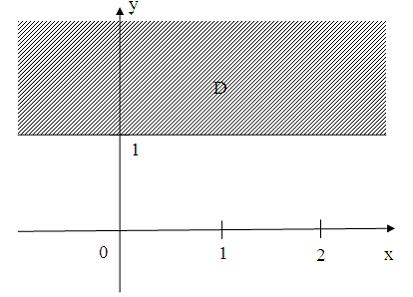
удовлетворяют условию …
 | 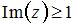 |
Тема: Дифференцирование функции комплексного переменного
Значение производной функции 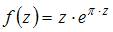 в точке
в точке 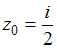 равно …
равно …
 | 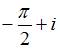 | ||
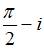 | |||
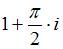 | |||
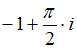 |
Решение:
Производная функции 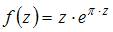 имеет вид
имеет вид