Модель простой линейной регрессии
Если функция регрессии линейная, то говорят о линейной регрессии. Линейная регрессия находит весьма широкое применение в эконометрике в связи с четкой экономической интерпретации ее параметров. Кроме того, построенное линейное уравнение может служить начальной точкой эконометрического анализа.
Простая линейная регрессия представляет собой линейную функцию между условным математическим ожиданием зависимой переменной  и одной зависимой переменной X (xi – значения зависимой переменной в i-ом наблюдении):
и одной зависимой переменной X (xi – значения зависимой переменной в i-ом наблюдении):
 . (5.5)
. (5.5)
Для отражения того факта, что каждое индивидуальное значение yi отклоняется от соответствующего условного математического ожидания, необходимо ввести в соотношение (5.5) случайное слагаемое ei:
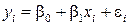 . (5.6)
. (5.6)
Это соотношение называется теоретической линейной регрессионной моделью; b0 и b1 – теоретическими коэффициентами регрессии. Таким образом, индивидуальные значения yi представляют в виде двух компонент – систематической ( 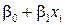 ) и случайной (ei). В общем виде теоретическую линейную регрессионную модель будем представлять в виде
) и случайной (ei). В общем виде теоретическую линейную регрессионную модель будем представлять в виде
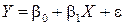 . (5.7)
. (5.7)
Основная задача линейного регрессионного анализа состоит в том, чтобы по имеющимся статистическим данным для переменных X и Y получить наилучшие оценки неизвестных параметров b0 и b1. По выборке ограниченного объема можно построить эмпирическое линейное уравнение регрессии:
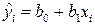 , (5.8)
, (5.8)
где 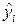 – оценка условного математического ожидания
– оценка условного математического ожидания 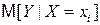 , b0 и b1 – оценки неизвестных параметров b0 и b1, называемые эмпирическими коэффициентами регрессии. Следовательно, в конкретном случае
, b0 и b1 – оценки неизвестных параметров b0 и b1, называемые эмпирическими коэффициентами регрессии. Следовательно, в конкретном случае
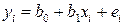 , (5.9)
, (5.9)
где отклонение ei – оценка теоретического случайного отклонения ei.
Задача линейного регрессионного анализа состоит в том, чтобы по конкретной выборке (xi,yi) найти оценки b0 и b1 неизвестных параметров b0 и b1 так, чтобы построенная линия регрессии была бы наилучшей в определенном смысле среди всех других прямых. Другими словами, построенная прямая 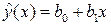 должна быть «ближайшей» к точкам наблюдений по их совокупности. Мерами качества найденных оценок могут служить определенные композиции отклонений ei. Например, коэффициенты b0 и b1 эмпирического уравнения регрессии могут быть оценены исходя из условия минимизации функции потерь (loss function):
должна быть «ближайшей» к точкам наблюдений по их совокупности. Мерами качества найденных оценок могут служить определенные композиции отклонений ei. Например, коэффициенты b0 и b1 эмпирического уравнения регрессии могут быть оценены исходя из условия минимизации функции потерь (loss function): 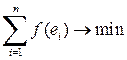 . Например, функции потерь могут быть выбраны в следующем виде:
. Например, функции потерь могут быть выбраны в следующем виде:
1) 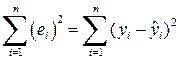 ; ; | 2) 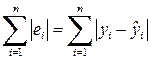 ; ; | 3) 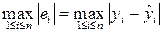 . . |
Самым распространенным и теоретически обоснованным является метод нахождения коэффициентов, при котором минимизируется первая сумма. Он получил название метод наименьших квадратов (МНК)[1]. Этот метод оценки является наиболее простым с вычислительной точки зрения. Кроме того, оценки коэффициентов регрессии, найденные МНК при определенных предпосылках, обладают рядом оптимальных свойств. Хорошие статистические свойства метода, простота математических выводов делают возможным построить развитую теорию, позволяющую провести тщательную проверку различных статистических гипотез. Минусы метода – чувствительность в «выбросам».
Метод определения оценок коэффициентов из условия минимизации второй суммы называется методом наименьших модулей. Этот метод обладает определенными достоинствами, например, по сравнению с методом наименьших квадратов он нечувствителен к выбросам (обладает робастностью). Однако у него имеются существенные недостатки. В первую очередь это связано со сложностью вычислительных процедур. Во-вторых, с неоднозначностью метода, т.е. разным значениям коэффициентов регрессии могут соответствовать одинаковые суммы модулей отклонений.
Метод минимизации максимума модуля отклонения наблюдаемого значения результативного показателя yi от модельного значения 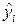 называется методом минимакса, а получаемая при этом регрессия минимаксной.
называется методом минимакса, а получаемая при этом регрессия минимаксной.
Среди других методов оценивания коэффициентов регрессии отметим метод максимального правдоподобия (ММП).
