Загруженных клеток, но не менее двух, считая и потенциальную; линии контура должны замкнуться в отрицательной клетке, из которой контур
взял свое начало; вершины перегиба линий контура должны лежать только в загруженных клетках и угол перегиба должен быть прямым, т.е. составлять 90°. Вершины перегибов линий контура обозначаются попеременно знаками плюс и минус, причем первый минус ставится в потенциальной клетке.
В каждой матрице из данной потенциальной клетки можно провести только один контур.
| Потребитель | Вспомога- тельные | Поставщик | ||||||
| Строка Столбец | А1 | А2 | А3 | Потребность в грузе, т | ||||
| Б1 | ||||||||
 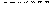 434 + 434 + |  _ (22) _ (22) | |||||||
| Б2 | -11 |  |  _ _ | |||||
| + 434 | ||||||||
| Б3 | -4 | _ | ||||||
 0 0 | (9) | + 210 | ||||||
| Б4 | -13 | |||||||
| Наличие груза, т |
Рисунок 6.-Матрица №6 с нанесённым контуром.
Следующим этапом решения задачи является отыскание минимального числового значения загрузки в клетках, где вершины контура имеют знак плюс. Наименьшая числовая загрузка в 210 единиц будет находиться в клетке
А3Б3. Минимальную загрузку в 210 единиц переносим из клетки со знаком плюс в клетку со знаком минус и добавляем к тому числу, которое там уже
имелось. Затем из следующей клетки со знаком плюс отнимаем это число и переносим далее по линии контура в клетку со знаком минус и так далее до потенциальной клетки.
Перенесем число 210 из клетки А3Б3 (+) в клетку А3Б2 (-) и добавим ее к той величине, которая в ней имелась. Тогда цифра загрузки в клетке А3Б3 будет равна нулю, а в клетке А3Б3 - 210 единицам. Из клетки А2Б2 (+) отнимаем число 210 и переносим ее в клетку А2Б1 (-), тогда в ней окажется загрузка, равная 210, а в А2Б2 останется 224. Из клетки А1Б1 (+) переносим число 210 в клетку А1Б3 (-).
Новый план закрепления получателей за поставщиками показан на матрице №7 (рисунок 7).
| Потребитель | Вспомога- тельные | Поставщик | ||||||
| Строка Столбец | А1 | А2 | А3 | Потребность в грузе, т | ||||
| Б1 | ||||||||
| Б2 | ||||||||
| Б3 | ||||||||
| Б4 | ||||||||
| Наличие груза, т |
Рисунок 7.-Матрица №7-улучшенный план закрепления получателей за поставщиками.
В результате проведенных действий произошло следующее; при переносе 210 единиц из клетки А3Б3 в клетку А3Б2 расстояние перевозки уменьшилось на 7 км (12-5=7); при переносе числа 210 из клетки А2Б2 в клетку А2Б1 расстояние перевозки уменьшилось на 11 км (17-6 = 11). Из клетки А1Б1 в А1Б3 уменьшилось на 4км (12-8=4).Таким образом, общее уменьшение расстояния перевозки 210 единиц груза составило 7+11+4=22
км, т.е. оно численно равно величине потенциала потенциальной клетки, из которой контур взял свое начало.
В связи с тем, что уменьшение расстояния перевозок численно равно потенциалу, контур следует начинать из клетки с наибольшим значением потенциала.
Продолжаем исследование матрицы №7. Проверяем ее на число загруженных клеток. Оно равно 6, т.е. соответствует правилу, при котором число загруженных клеток должно быть равно 4+3-1=6.
Пользуясь предыдущими правилами, отыскиваем вспомогательные коэффициенты строки и столбца и подставляем их в матрицу. Такими коэффициентами будут :для Б1- 0; Б2-11; БЗ- (-4); Б4-9; А1-12; А2-6; А3-(-6).
Проверяем матрицу на потенциальность и устанавливаем, что в ней имеется две потенциальные клетки: А1Б2; А1Б4; (матрица №8, рисунок 8). Строим контур, который выйдет из клетки А1Б2, т.к. это клетка с наибольшим потенциалом, пойдет в клетки А2Б2, А2Б1, А1Б1 и замкнется в клетке А2Б2. На вершинах контура проставляем знаки минус и плюс, причем первый минус ставится в потенциальной.
| Потребитель | Вспомога- Тельные | Поставщик | ||||||
| Строка Столбец | А1 | А2 | А3 | Потребность в грузе, т | ||||
| -6 | ||||||||
| Б1 | _ | |||||||
 224+ 224+ | ||||||||
| Б2 | -11 | |||||||
| (10) _ | + 224 | |||||||
| Б3 | -4 | |||||||
| Б4 | ||||||||
| (9) | ||||||||
| Наличие груза, т |
Рисунок 8.-Матрица №8- с нанесенным контуром
В результате проведенных действий произошло следующее; при переносе 224 единиц из клетки А2Б2 в клетку А2Б1 расстояние перевозки уменьшилось на 11 км (17-6=11); при переносе числа 224 из клетки А1Б1 в клетку А1Б2 расстояние перевозки увеличилось на 1 км (12-13=-1). Таким образом, общее уменьшение расстояния перевозки 224 единиц груза составило 11-1=10 км, т.е. оно численно равно величине потенциала потенциальной клетки, из которой контур взял свое начало.
В связи с тем, что уменьшение расстояния перевозок численно равно потенциалу, контур следует начинать из клетки с наибольшим значением потенциала.
Продолжаем исследование матрицы №8. Проверяем ее на число загруженных клеток. Оно равно 5, т.е. не соответствует правилу, при котором число загруженных клеток должно быть равно 4+3-1=6. Вводим нулевую загрузку в А1Б4.
Пользуясь предыдущими правилами, отыскиваем вспомогательные коэффициенты строки и столбца и подставляем их в матрицу. Такими коэффициентами будут для Б1- 0; Б2-10; БЗ-5; Б4-9; А1-3; А2-6; А3-(-5).
Новый план закрепления получателей за поставщиками показан на матрице №9 (рисунок 9).
| Потребитель | Вспомога- тельные | Поставщик | ||||||
| Строка Столбец | А1 | А2 | А3 | Потребность в грузе, т | ||||
| -5 | ||||||||
| Б1 | ||||||||
| Б2 | ||||||||
| Б3 | ||||||||
| Б4 | ||||||||
| Наличие груза, т |
Рисунок 9.-Матрица №9-оптимальный план закрепления получателей за поставщиками.
Проверяем матрицу на потенциальность. В матрице №9 нет потенциальных клеток, что свидетельствует о получении оптимального плана закрепления получателей за поставщиками.
1. Поставщик А1 будет поставлять продукцию потребителю Б3 в количестве 210 единиц на расстояние 8 км и потребителю Б2 в количестве 224 единицы на расстояние13 км;
2. Поставщик А2 будет поставлять продукцию потребителю Б1 в количестве 434 единицы на расстояние 6 км и потребителю Б4 в количестве 196 единицы на расстояние15 км;
3. Поставщик А3 будет поставлять продукцию потребителю Б2 в количестве 210 единиц на расстояние 5 км
Расшифрованный оптимальный план перевозок передают в диспетчерскую для определения дневных заданий шоферам и выписки путевых листов.
Рассмотрим итоги решения задачи на закрепление получателей за поставщиками.
Среднее расстояние перевозки груза определяется:
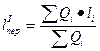 , (9)
, (9)
где Q – количество перевозимого груза, указанного в клетке рассматриваемой матрицы, т;
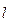 - расстояние между поставщиком и получателем, соответствующие грузу Q, км.
- расстояние между поставщиком и получателем, соответствующие грузу Q, км.
Уменьшение среднего расстояния перевозки в процентах определяется:
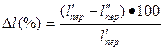 , (10)
, (10)
где 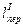 и
и 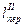 - среднее расстояние перевозки, соответственно, при первичном и улучшенном плане закрепления получателем за поставщиками, км
- среднее расстояние перевозки, соответственно, при первичном и улучшенном плане закрепления получателем за поставщиками, км
При первичном плане закрепления получателей за поставщиками среднее расстояние перевозки
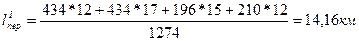 ;
;
при вторичном плане
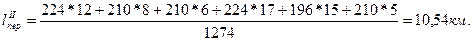
уменьшение среднего расстояния перевозки при вторичном плане закрепления составило
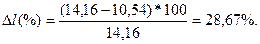
Каждый последующий вариант закрепления получателей за поставщиками дает все меньшие значения уменьшения среднего расстояния перевозки и поэтому при решении сложных и громоздких задач можно не добиваться оптимального варианта, а ограничиться двумя-тремя вариантами улучшении плана.
В практике решения задач матрицу наносят на плотный лист бумаги, цифры в нее проставляют карандашом, при переносе цифр ненужные стирают, а вместо них записывают новые. Таким образом, вся задача решается на одной матрице в описанной ранее последовательности.
При оптимальном плане закрепления среднее расстояние перевозки составит:
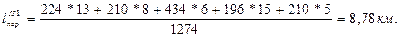
уменьшение среднего расстояния перевозки при оптимальном плане закрепления составило