Первой ступени высшего образования
1. Основные операции над множествами.
2. Отображения.
3. Элементы комбинаторики. Бином Ньютона.
4. Комплексные числа. Операции над комплексными числами.
5. Формула Муавра. Извлечение корня из комплексного числа.
6. Векторы. Линейные операции над векторами. Проекция вектора на ось.
7. Линейная зависимость векторов. Базис. Координаты вектора в базисе.
8. Декартовы прямоугольные координаты в пространстве. Координаты точек. Координаты векторов.
9. Направляющие косинусы. Скалярное произведение.
10. Векторное произведение. Смешанное произведение.
11. Прямая. Уравнения прямой.
12. Взаимное расположение прямых.
13. Плоскость. Нормальное уравнение плоскости.
14. Плоскость. Взаимное расположение плоскостей.
15. Кривые второго порядка. Эллипс. Гипербола. Парабола.
16. Исследование на плоскости уравнения второй степени.
17. Понятие евклидова пространства. Размерность и базис векторного пространства.
18. Матрицы. Основные понятия. Операции над матрицами.
19. Матрицы. Определитель матрицы. Обратная матрица. Ранг матрицы.
20. Понятие линейного оператора. Переход к новому базису. Линейное преобразование переменных.
21. Собственные значения и собственные вектора матриц.
22. Многочлены. Теорема о делении с остатком. Теорема Безу.
23. Квадратичные формы.
24. Канонический базис квадратичной формы. Канонический базис из собственных векторов матрицы квадратичной формы. Канонический базис Якоби.
25. Знакоопределенные квадратичные формы.
26. Применение квадратичных форм к исследованию кривых второго прядка.
27. Системы линейных уравнений. Критерий совместности системы линейных уравнений.
28. Системы линейных уравнений. Правило Крамера решения систем линейных уравнений. Метод Гаусса. Однородные системы уравнений. Разрешенные системы линейных уравнений.
29. Функции. Основные понятия.
30. Понятие числовой последовательности. Сходящиеся последовательности
31. Бесконечный предел. Замечательные пределы. Принцип сходимости.
32. Предел функции. Теорема Гейне.
33. Односторонние пределы. Пределы на бесконечности Бесконечные пределы.
34. Непрерывность функции. Непрерывность композиции. Точки разрыва.
35. Определение и смысл производной. Построение касательной к графику функции.
36. Экономический смысл производной. Эластичность функции.
37. Дифференцируемость функции. Правила дифференцирования. Таблица производных
38. Производная сложной функции. Производная обратной функции.
39. Дифференциал. Приближенные вычисления.
40. Свойства дифференцируемых функций. Правила Лопиталя.
41. Производные высших порядков.
42. Исследование функций. Основные понятия.
43. Монотонность функции. Локальный экстремум. Исследование стационарных точек.
44. Глобальный экстремум. Выпуклость и перегибы графика функции.
45. Исследование функции и построение графика
46. Интерполяция функций. Интерполяционный полином Лагранжа.
47. Аппроксимация функций. Формула Тейлора. Основные разложения.
48. Пространство 
. Точки, расстояние. Множества в .
49. Последовательности в 
. Сходимость.
50. Функции в . Предел. Теорема Гейне.
51. Непрерывность функции в . Непрерывность на множестве. Теоремы о непрерывности.
52. Дифференцируемость функций в . Частные производные.
53. Дифференциал функции нескольких переменных. Необходимые условия дифференцируемости. Достаточные условия.
54. Дифференцирование функции, заданной неявно и композиции функций.
55. Полные дифференциалы и частные производные высших порядков. Признак полного дифференциала. Формула Тейлора.
56. Локальный экстремум функции нескольких переменных. Необходимое и достаточное условия. Исследование стационарных точек.
57. Условный экстремум функций нескольких переменных. Глобальный экстремум.
58. Понятие неопределенного интеграла. Свойства неопределенного интеграла.
59. Замена переменных. Интегрирование по частям.
60. Интегрирование рациональных функций. Метод рационализации.
61. Вычисление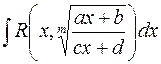 
. Вычисление 
.
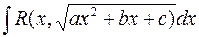62. Вычисление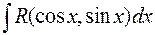 
. Вычисление 
.
63. Определенные интегралы. Интегральные суммы. Необходимое и достаточное условие интегрируемости.
64. Равномерно непрерывные функции. Интегрируемость непрерывных, разрывных и монотонных функций.
65. Основные свойства определенного интеграла. Формулы среднего значения. Основные правила интегрирования. Приложения определенного интеграла (площадь плоской фигуры, объемы тел вращения).
66. Несобственные интегралы. Интегрирование неограниченных функций. Интегрирование по бесконечному промежутку.
67. Понятие кратного интеграла. Интегрирование функций многих переменных
68. Ряды. Положительные ряды. Знакочередующиеся ряды. Абсолютная сходимость.
69. Функциональные ряды. Степенной ряд.
70. Дифференциальные уравнения. Основные понятия
71. Дифференциальные уравнения первого порядка.
72. Дифференциальные уравнения семейства кривых. Геометрическое истолкование дифференциального уравнения. Задача Коши
73. Дифференциальные уравнения с разделяющимися переменными.
74. Однородные дифференциальные уравнения. Линейные дифференциальные уравнения
75. Дифференциальные уравнения второго порядка. Задача Коши
76. Интегрируемые типы дифференциальных уравнений второго порядка. Случаи понижения порядка.
77. Общие свойства решений линейных однородных дифференциальных уравнений второго порядка
78. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
79. Линейные неоднородные уравнения второго порядка с постоянными коэффициентами.
80. Линейные дифференциальные уравнения n–го порядка. Понятие случайного эксперимента.
81. Пространство элементарных событий. Достоверное и невозможное событие.
82. Операции над событиями (сумма, разность, произведение). Совместные и несовместные события. Противоположное событие.
83. Свойства операций над событиями.
84. Алгебра и s - алгебра событий.
85. Классическое определение вероятности события.
86. Статистическое определение вероятности события.
87. Геометрические вероятности.
88. Понятие о полной группе событий.
89. Формулы сложения вероятностей для несовместных и совместных событий.
90. Условная вероятность. Формула умножения вероятностей. Независимость событий.
91. Формула полной вероятности.
92. Формула Байеса.
93. Основные понятия комбинаторики. Правила суммы и произведения. Перестановки, размещения, сочетания и формулы для их вычисления.
94. Схема независимых испытаний Бернулли. Наивероятнейшее число наступления событий в схеме Бернулли.
95. Теорема Пуассона.
96. Локальная теорема Муавра – Лапласа.
97. Интегральная теорема Муавра – Лапласа.
98. Случайная величина и ее функция распределения. Свойства функции распределения.
99. Непрерывные и дискретные случайные величины.
100. Математическое ожидание случайной величины и его свойства.
101. Дисперсия случайной величины и ее свойства. Среднеквадратическое отклонение.
102. Примеры распределений случайной величины: биномиальное, Пуассона, равномерное, показательное.
103. Биномиальное распределение, его математическое ожидание и дисперсия.
104. Распределение Пуассона, его математическое ожидание и дисперсия.
105. Равномерное распределение, его математическое ожидание и дисперсия.
106. Показательное распределение, его математическое ожидание и дисперсия.
107. Нормальное распределение. Свойства функции Гаусса.
108. Функция Лапласа и ее свойства. Вероятность попадания нормальной случайной величины в заданный интервал.
109. Отклонение нормальной случайной величины от ее математического ожидания. Правило ”трех сигм”
110. Совместная функция распределения двух случайных величин. Независимые случайные величины. Математическое ожидание и дисперсия независимых случайных величин.
111. Плотность совместного распределения вероятностей непрерывной двумерной случайной величины. Свойства двумерной плотности вероятности.
112. Корреляционный момент и коэффициент корреляции.
113. Выборочный метод и его основные понятия. Случайная выборка, объем выборки.
114. Вариационный ряд для дискретных и непрерывных случайных величин. Полигон и гистограмма.
115. Эмпирическая функция распределения и ее свойства.
116. Статистические оценки параметров распределения. Состоятельность и несмещенность статистических оценок.
117. Выборочные среднее и дисперсия и их свойства.
118. Надежность и доверительный интервал.
119. Доверительный интервал для математического ожидания нормального распределения при известной дисперсии.
120. Доверительный интервал для математического ожидания нормального распределения при неизвестной дисперсии
121. Доверительный интервал для оценки среднего квадратического отклонения s нормального распределения
122. Проверка статистических гипотез. Нулевая и альтернативная гипотезы, статистический критерий. Ошибки первого и второго рода.
123. Этапы проверки статистической гипотезы.
124. Критерий согласия Пирсона о виде распределения.
125. Понятие о регрессионной зависимости случайных величин. Парная и множественная регрессии.
126. Выборочные уравнения регрессии.
127. Линейная регрессия. Нахождение коэффициентов линейной регрессии методом наименьших квадратов.
128. Понятие о множественной линейной регрессии.
129. Корреляционная матрица.
130. Понятие о парной линейной корреляции.
131. Понятие о парной нелинейной корреляции. Индекс корреляции.
132. Оценка значимости параметров парной линейной регрессии.
133. Понятие о множественной корреляции.
134. Нелинейная регрессия. Логарифмическая, обратная, степенная, и показательные модели нелинейной регрессии.
135. Понятие о цепях Маркова. Однородные цепи Маркова. Переходные вероятности. Матрица перехода.
136. Равенство Маркова. Расчет вероятностей состояния системы с использованием матрицы перехода.
137. Понятие о цепях Маркова с непрерывным временем.
138. Уравнения Колмогорова. Финальные вероятности цепей Маркова с непрерывным временем
139. Понятие о схеме гибели и размножения. Расчет вероятностей состояний.
140. Понятие о системах массового обслуживания.
141. Одноканальная система массового обслуживания с отказами.
142. Одноканальная система массового обслуживания с ожиданием.
143. Понятие о многоканальных системах массового обслуживания. Многоканальная модель с отказами.