Лінійна залежність системи векторів.

Базис і розмірність векторного простору

Лінійна залежність системи векторів визначається так само, як лінійна залежність системи рядків матриці, які є числовими векторами.

Означення. Лінійною комбінацією векторів векторного простору називається вектор вигляду

. (1)

де 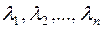– деякі дійсні числа (коефіцієнти лінійної комбінації).

Означення. Система векторів 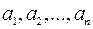векторного простору 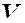називається лінійно залежною, якщо існують числа 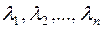, які не всі водночас дорівнюють нулю ( ), такі що

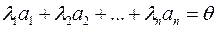(2)

Система векторів 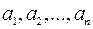називається лінійно незалежною, якщо остання рівність виконується тільки в одному випадку , коли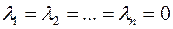

Теорема. (про лінійну залежність векторів)

Вектори 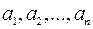лінійно залежні тоді і тільки тоді, коли один з векторів цієї системи є лінійною комбінацією інших.

Означення. Впорядкована система векторів 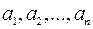називається базисом векторного простору 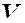, якщо

1) вона лінійно незалежна;

2) кожен вектор 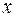простору 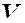лінійно виражається через вектори цієї системи, тобто .

Означення. Векторний простір 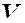називається 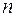-вимірним, якщо в ньому існує базис з 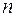елементів. Число 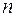називається розмірністю простору і позначається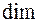 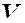. Простір скінченної розмірності називається скінченновимірним. Простір, в якому можна знайти будь-яке число лінійно незалежних векторів називається нескінченновимірним. (Лінійна алгебра вивчає тільки скінченновимірні простори.)

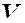Теорема (про зв'язок між базисом і розмірністю). Система векторів утворює в просторі розмірності 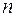базис тоді і тільки тоді, коли вона лінійно незалежна, а число векторів в ній дорівнює розмірності простору .

Координати вектора у векторному просторі.

Розкладання вектора за базисом .

Нехай 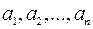– деякий базис векторного простору 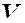. Тоді будь-який вектор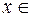 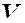можна подати у вигляді (1)

де 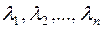– деякі дійсні числа, причому єдиним чином. В цьому випадку вираз (1) називається розкладом вектора 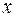за базисом .

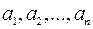Означення. Коефіцієнти розкладу (1) називаються координатами вектора в даному базисі. Упорядкований набір координат вектора називається його координатним рядком і позначається :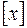

.

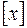
Приклад.Довести, що вектори утворюють базис у просторі 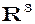та знайти координати вектора 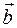в цьому базисі.

, , ,

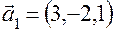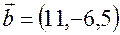
Розв’язання. 1) Перевіримо необхідну і достатню умову компланарності векторів :

.

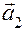
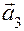
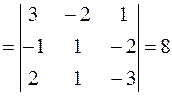Оскільки 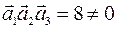, то вектори некомпланарні, тому вони лінійно незалежні і утворюють базис.

2) Розкладемо вектор за базисом :

або в координатному вигляді:

.

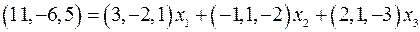Вектори рівні, коли їх відповідні координати рівні. Тому одержимо систему:

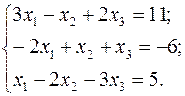
Розв’язуючи цю систему будь-яким способом, знайдемо

, , .

3) Отже, .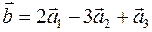

.

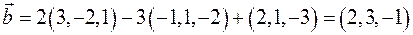Відповідь: