Классы интегрируемых функций 3 страница

Все эти утверждения доказываются либо непосредственно из определения предела функции, либо ссылкой на то, что аналогичные утверждения верны для последовательностей и Теорему 3.1.

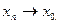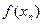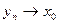
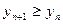
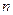Докажем, например,3.1.8.Пусть выполнены условия 3.1.8,и пусть монотонно возрастая. Тогда монотонно возрастает и ограничена сверху, и, значит, имеет предел А. Пусть , для всех ,тоже монотонно возрастая. Тогда последовательность 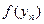тоже будет монотонно возрастающей и ограниченной и, значит, будет иметь предел В. Но 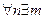такое, что 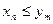,и ,значит, 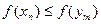,откуда 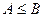.По аналогичной причине, 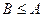.Следовательно, 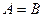, и всё доказано.(Почему? Что будет, если 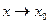, не монотонно?)

3.3. Нечто об эквивалентности и 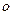- малых.

Пусть при 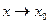(где может быть и бесконечностью, 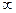) 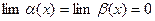или оба этих предела равны .

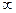Определение 3.3.Пишут 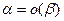, если 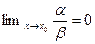,( и говорят, что (при 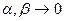) 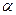убывает быстрее, чем 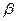, или что (при 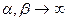) 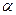растёт медленнее, чем ).

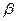Это определение можно использовать и при условии, что 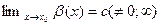.В этом случае равенство 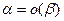означает, что 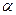- б.м. при 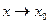.(Почему?).Тот же факт можно записать как 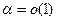.Вообще, выражение 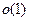может (при нашем определении символа 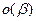) означать только б.м.

Лемма 3.3.1.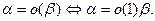

Доказательство. Оба равенства означают, .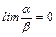

Лемма 3.3.2. (1) 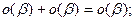(2) 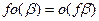;(3) при 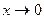имеет место включение 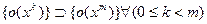; при 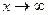включение обратное.

Определение 3.4.При 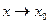пишут, что 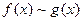,если и только если 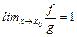.Говорят, что в этом случае 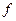и 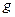эквивалентны.

Лемма 3.3.3. .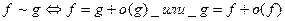

Проверяется по определению.

Лемма 3.3.4. При вычислении пределов произведений и частных функции можно заменять на эквивалентные.

Доказательство. Пусть 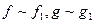,и 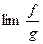существует. Тогда 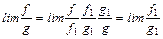(по 3.1.1);для произведения – аналогично

4.Непрерывность.

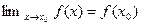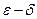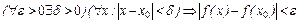Определение 4.1.Функция называется непрерывной в точке ,если она определена в некоторой окрестности этой точки и . 1.Определение непрерывности по :функция называется непрерывной в точке ,если она определена в некоторой окрестности точки и для точек из этой окрестности . 2.Определение непрерывности с помощью окрестностей: называется непрерывной в точке ,если для всякой .

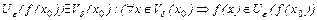Понятно, что все эти определения эквивалентны. Они означают, что по любой окрестности точки 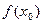можно найти окрестность точки ,которая при отображении с помощью функции 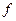целиком попадает в выбранную заранее окрестность точки 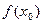.Иными словами, при малом изменении мало меняется

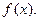
Свойства 3.1.5 – 3.1.7 имеют место для непрерывных функций при естественных переформулировках. Один факт отметим специально.

Теорема 4.1. Если функции и 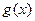определены в некоторой окрестности точки и непрерывны в точке , то в этой точке будут непрерывны и функции 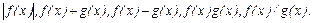(последняя – при естественном ограничении ).

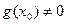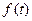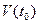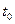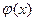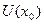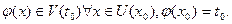Определение 4.2.Пусть функция определена в некоторой окрестности точки , а функция - в некоторой окрестности точки , и пусть Функция 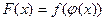, определённая в окрестности 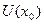, называется сложной функцией от

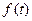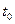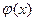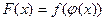Теорема 4.2.Если непрерывна в точке , а - в точке , то непрерывна в точке .

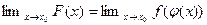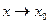
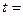
Доказательство. Нам нужно вычислить .При 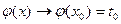(по непрерывности 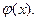). Для функции 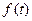это значит(по непрерывности 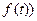, что она стремится к 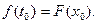Теорема доказана.

Примечание. (Точки разрыва).Если не является непрерывной в точке ,хотя и определена в некоторой окрестности этой точки(включая саму эту точку или нет), говорят, что функция разрывна в точке .Если при этом существуют односторонние (конечные!) пределы 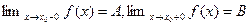, говорят, что функция имеет в разрыв первого рода (скачок); при 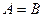разрыв называется устранимым. Если хотя бы один из этих пределов не существует (в частности, равен 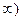, разрыв называется разрывом второго рода.

Примеры:(1) 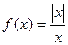- в 0 разрыв первого рода;(2) 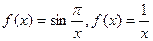- разрывы в 0 второго рода.

4.3.Свойства функций, непрерывных на отрезке

Определение 4.3.Функция называется непрерывной на множестве 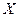(открытом), если она непрерывна в каждой точке этого множества. Функция называется непрерывной на замкнутом множестве 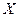,если она непрерывна на внутренности этого множества и если 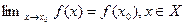.Для отрезка 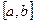это означает, что 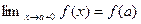и 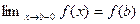.То, что непрерывна на множестве 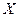, обозначается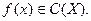

Далее следуют утверждения, которые, с одной стороны, помогут в дальнейшем доказывать разные теоремы о более сложных объектах, а с другой стороны показывают, что естественное понятие непрерывности не противоречит математическому.

Теорема 4.3(1-ая Вейерштрасса).

Если 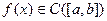, то она ограничена на 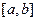(т.е., найдутся такие числа 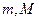, что

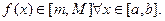
Доказательство. Докажем, что существует 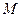.Если это не так, то 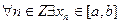,такой что 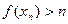. Последовательность 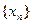ограничена, следовательно у неё есть предельная точка .Пусть 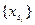- подпоследовательность, сходящаяся к .В силу непрерывности функции , последовательность 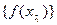будет сходиться к 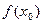.В силу выбора последовательности 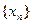,подпоследовательность 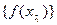бесконечнобольшая. Противоречие доказывает существование 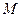. Аналогично доказывается существование 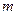. Теорема доказана.

Теорема 4.4(2-ая Вейерштрасса). Если 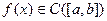, то она достигает на 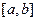максимума и минимума.

Доказательство. Докажем про максимум. Пусть 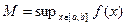. 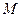существует по Теореме 4.3.Докажем, что найдётся точка 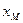, для которой 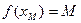. Если это не так, то функция 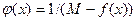непрерывна на 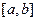. По теореме 4.3, 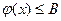для некоторого 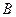. Тогда 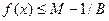, что противоречит выбору 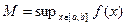.Противоречие доказывает теорему.

Теорема 4.5(1-ая Коши) Если 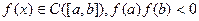,то существует точка 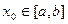, для которой .

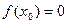Доказательство. Пусть ,для определённости, 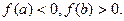Построим последовательность стягивающихся отрезков. Пусть 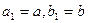; поделим 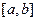пополам, получим точку 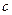. Может быть два случая: либо 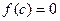,и мы нашли точку 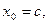,в которой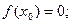 либо на концах одной из половин первоначального отрезка принимает значения разных знаков, обозначим левый конец этой половины 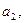правый - 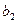. В первом случае теорема для доказана, во втором будем делить пополам отрезок 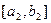.Продолжая этот процесс, мы либо найдём точку , в которой 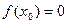, и в этом случае теорема будет доказана, либо получим последовательность 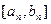стягивающихся отрезков, по длине стремящихся к нулю, и таких, что 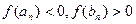.Пусть - общая точка этих отрезков. Она принадлежит всем этим отрезкам, и , в частности, отрезку 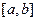; значит, она в точке непрерывна( если это внутренняя точка отрезка 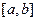, то просто непрерывна; если это 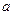,то непрерывна справа; если 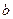, то непрерывна слева). Рассмотрим 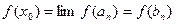.Согласно первому из этих равенств, 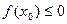, согласно второму - 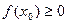. Значит, 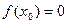, и теорема доказана.

Теорема 4.6(2-ая Коши). Если 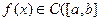, то

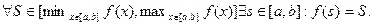
Доказательство. Рассмотрим 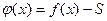. Очевидно, 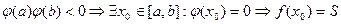. Положим 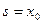.Теорема доказана.

Теорема 4.7(о существовании обратной функции). Пусть функция 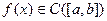и строго монотонна. Тогда на 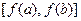однозначно определена функция 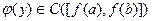, такая, что .

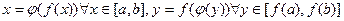Доказательство.1.Определение 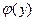.Пусть 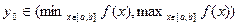.Согласно 2-ой теореме Коши, 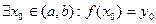.Такой только один. Равенство 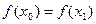при 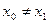противоречит строгой монотонности . Положим .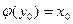

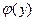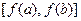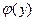Этим уравнением функция определена однозначно на всём отрезке (Почему на всём?). 2. Непрерывность . Пусть, по-прежнему, 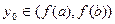и пусть 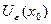целиком принадлежит 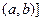.Такое заведомо существует, потому что - внутренняя точка отрезка 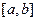.Пусть 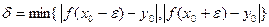.Тогда 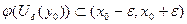.Мы по 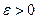нашли 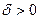,такое, что при отображении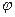 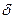-окрестность точки 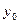целиком отображается в -окрестность точки 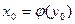.Непрерывность на 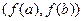доказана .Непрерывность слева и справа в 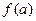и 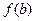(с одной стороны!) доказывается аналогично. Теорема доказана(позже мы докажем её ещё раз как следствие теоремы о неявной функции).

Определение 4.4.Функция называется равномерно-непрерывной на множестве 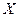, если 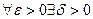,такое, что, как только 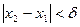, будет выполняться неравенство .

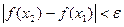Теорема 4.8(Кантора).Если 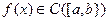,то на 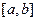равномерно-непрерывна.

Доказательство. Предположим, что это не так. Тогда существует некоторое 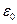, для которого при любой последовательности 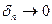всегда найдётся пара точек 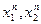, для которых 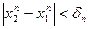и 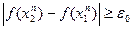.Пусть - предельная точка последовательности 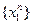.Чтобы не вводить дополнительные индексы,предположим,что 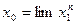.Тогда и 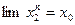(в силу условия 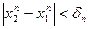) Но в этом случае 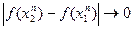,что противоречит предположению 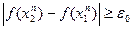.Теорема доказана

5.Дифференцируемые функции

Определение 5.1.Функция называется дифференцируемой в точке , если она определена в некоторой окрестности этой точки, и если её приращение в этой точке может быть записано в виде

,

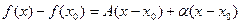где 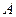- константа, не зависящая от точки , а 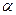- бесконечномалая при .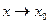