Понятие предела функции
А.С. Березина, Л.Н. Гавришина, А.Г. Седых
МАТЕМАТИЧЕСКИЙ АНАЛИЗ:
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Учебное пособие
Кемерово 2012
УДК 510.2(076)
ББК 74.262
Б48
Рецензенты:
Н.К. Смоленцев, доктор физ.-мат. наук,
профессор кафедры математического анализа
Кемеровского государственного университета;
П.Н. Подкур,канд. физ.-мат. наук, доцент
кафедры высшей и прикладной математики
Кемеровского института (филиал) РГТЭУ
Б48 Березина А.С. Математический анализ: дифференциальное исчисление [Текст] : учебное пособие / А.С. Березина, Л.Н. Гавришина, А.Г. Седых ; Кемеровский институт (филиал) РГТЭУ. − Кемерово : Кемеровский институт (филиал) РГТЭУ, 2012. – 68 с.
Содержит теоретический материал, необходимый для решения практических заданий, примеры решения типовых задач, варианты контрольной работы, задачи для практических занятий; предложен контрольный тест для самопроверки и список контрольных вопросов.
Предназначено для студентов экономического факультета всех форм обучения.
УДК 510.2(076)
ББК 74.262
© Кемеровский институт (филиал) РГТЭУ, 2012
Оглавление
Введение. 4
1 Понятие функции. 6
2 Предел функции. 8
2.1 Понятие предела функции. 8
2.2 Правила вычисления пределов. 11
2.3 Непрерывность функции. 16
3 Производная функции. 18
3.1 Понятие производной и дифференциала. 18
3.2 Правила дифференцирования. 20
4 Использование производных для исследования функций. 23
4.1 Возрастание, убывание функции. Точки экстремума. 23
4.2 Выпуклость, вогнутость функции. Точки перегиба. 24
4.3 Асимптоты графика функции. 25
4.4 Общая схема исследования функции. 26
5 Применение производной в экономических задачах. 29
5.1 Предельные показатели в экономике. 29
5.2 Понятие эластичности. 30
5.3 Оптимальное значение экономических функций. 32
6 Функция двух переменных. 33
6.1 Частные производные. Градиент. 33
6.2 Экстремум функции двух переменных. 35
6.3 Условный экстремум функции двух переменных. 36
7 Варианты контрольной работы.. 38
8 Методические указания для выполнения контрольной работы.. 43
9 Контрольные вопросы для зачета. 51
10 Контрольный тест для самопроверки. 53
11 Задачи для самостоятельного решения. 58
11.1 Понятие функции. 58
11.2 Предел функции. 60
11.3 Непрерывность функции. 61
11.4 Производная функции. 61
11.5 Приложение производной. 63
11.6 Применение производной в экономике. 64
11.7 Функция многих переменных. 66
Список литературы.. 67
Ведение
По государственному образовательному стандарту дисциплина «Математический анализ» относится к обязательным базовым дисциплинам.
Цель изучения дисциплины состоит, во-первых, в изучении основ математического анализа, формировании предусмотренных учебной программой компетенций. Во-вторых, в результате изучения математики студенты должны развить, в частности такие навыки и умения, как логическое мышление, поиск рационального решения любой проблемы.
Процесс изучения дисциплины направлен на формирование следующих компетенций:
· Владение культурой мышления, способность к обобщению, анализу, восприятию информации, постановки цели и выбору пути ее достижения.
· Способность к саморазвитию, повышению квалификации и мастерства.
· Способность собрать и проанализировать исходные данные, необходимые для расчета экономических и социально-экономических показателей, характеризующих деятельность хозяйствующих субъектов.
· Способность осуществлять сбор, анализ и обработку данных, необходимых для решения поставленных экономических задач.
· Способность выбрать инструментальные средства для обработки экономических данных в соответствии с поставленной задачей, проанализировать результаты расчетов и обосновать полученные выводы.
· Способность использовать для решения аналитических и исследовательских задач современные технические средства и информационные технологии.
Говоря словами М.В. Ломоносова, «Математику уже затем учить следует, что она ум в порядок приводит».
Освоение курса предполагает, помимо посещения лекций и практических занятий, самостоятельную работу студентов с изучаемым материалом, половина часов отведенных на изучение предмета приходится на самостоятельную работу. Это следует иметь в виду студентам, приступающим к изучению предмета.
В результате изучения дисциплины студент должен:
- Знать:Основные понятия методы математического анализа, дифференциальных уравнений.
- Уметь: использоватьосновные методы математического анализа и дифференциальные уравнения в практической деятельности.
- Владеть:Навыками математического анализадля исследования и решения экономических задач.
Для того чтобы успешно освоить учебную программу рекомендуем процесс обучения реализовывать в следующей последовательности:
1) хорошо ознакомиться с теоретическим материалом, запомнить формулы и правила, необходимые для решения задач. На этом этапе можно воспользоваться опорным конспектом в данном пособии и учебником. Для запоминания рекомендуем несколько раз написать формулы на бумаге и произнести правила вслух. При этом работает зрительная, моторная и слуховая память;
2) решение примеров по теме рекомендуем начинать с наиболее простых задач и поэтапно переходить к более сложным задачам.
При подготовке к коллоквиуму по теме или экзамену для самоконтроля усвоения учебного материала рекомендуем воспользоваться контрольным тестом.
Для студентов заочного обучения в пособии приведены варианты контрольной работы, номер варианта совпадает с последней цифрой зачетной книжки.
Понятие функции
Математика - это наука о пространственных формах и количественных отношениях действительного мира. К основным понятиям математики относится понятие - величина. Под величиной понимается все, что может быть измерено в окружающем нас мире. В математике безразлична физическая сущность величины. Поэтому выводы математики применимы ко всем величинам вообще. Величины бывают постоянные и переменные. Между переменными величинами может существовать функциональная зависимость.
Переменная величина y называется функцией от переменной величины x ,если каждому значению величины x по некоторому правилу ставится в соответствие определенное значение величины y.
Это обозначается, как 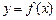 , при этом величина x называется независимой переменной (аргументом), а y - зависимой переменной, или функцией от
, при этом величина x называется независимой переменной (аргументом), а y - зависимой переменной, или функцией от 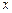 .
.
Каждая функция имеет свою область определения, под которой понимается множество всех возможных значений аргумента.
Пример 1.1. Найти область определения функции
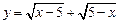 .
.
Решение. Так как функция представляет собой сумму функций, то область определения функции будет состоять из всех тех значений 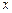 , которые принадлежат одновременно области определения функций
, которые принадлежат одновременно области определения функций 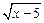 и
и 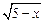 . Поэтому область определения данной функции определяется как совокупность значений
. Поэтому область определения данной функции определяется как совокупность значений 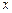 , при которых одновременно выполняются неравенства
, при которых одновременно выполняются неравенства 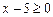 и
и 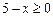 . Это будет значение
. Это будет значение 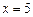 .
.
Существует три способа задания функций.
1.Аналитический способ задания функции состоит в том, что соответствие между переменными задается с помощью формулы, например,
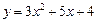 ,
, 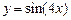 .
.
В общем виде это записывается как 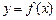 или
или 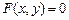 . Во втором случае говорят, что функция задана неявно.
. Во втором случае говорят, что функция задана неявно.
Функция называется сложной, если ее аргумент сам является функцией: 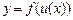 .
.
В этом случае 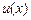 называется промежуточным аргументом.
называется промежуточным аргументом.
Пример 1.2. Представить сложную функцию 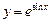 в виде цепочки элементарных функций.
в виде цепочки элементарных функций.
Решение. Пусть 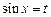 , тогда получим элементарную функцию
, тогда получим элементарную функцию 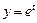 .
.
Пусть на некотором множестве Х задана функция у = f(x) и Y - область значения данной функции.
Возьмем некоторое число 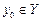 . Тогда найдется такое число
. Тогда найдется такое число  (возможно не единственное), что
(возможно не единственное), что 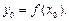 Таким образом, каждому значению
Таким образом, каждому значению 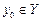 поставлено в соответствие число
поставлено в соответствие число  (возможно не единственное). Если такое число
(возможно не единственное). Если такое число  - единственное, то говорят, что задана функция х = g(y), которая называется функцией обратной к данной. Например, функция
- единственное, то говорят, что задана функция х = g(y), которая называется функцией обратной к данной. Например, функция 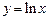 имеет обратную функцию
имеет обратную функцию 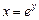 .
.
2.Табличный способ задания функции состоит в том, что соответствие между переменными задается в виде таблицы.
Например,
| x | ||||||||
| y |
Эту же функцию можно записать формулой y=x2.
3.Графический способ задания функции состоит в том, что соответствие между переменными задается в виде графика (рисунок 1.1).
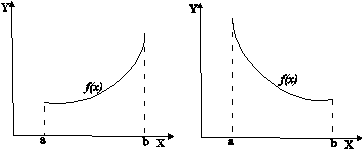 а) б) Рисунок 1.1 – График функции а) б) Рисунок 1.1 – График функции 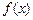 : а) : а) 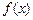 - возрастающая функция, б) - возрастающая функция, б) 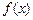 - убывающая функция - убывающая функция |
График функции может быть симметричен относительно оси Y, если она четная, т.е. f(-x)=f(x). График функции может быть симметричен относительно начала координат, если она нечетная т.е. f(-x)=-f(x).
Предел функции
Понятие предела функции
Во многих практических задачах требуется определить скорость изменения функции при изменении аргумента. В этом случае используется понятие производной функции. Это понятие в свою очередь вводится с помощью понятия предела функции. Поясним смысл понятия предела на примере.
Функция 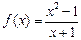 не определена при значении
не определена при значении 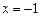 , так как при нем знаменатель обращается в нуль. Таким образом, при
, так как при нем знаменатель обращается в нуль. Таким образом, при 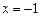 функция имеет разрыв (рисунок 2.1).
функция имеет разрыв (рисунок 2.1).
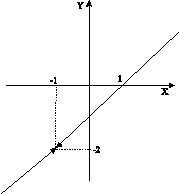 Рисунок 2.1 – Функция Рисунок 2.1 – Функция 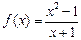 |
Однако если положить значение функции в точке 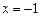 равным
равным 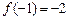 , то получим функцию непрерывную на всей числовой оси. Математически это записывается как
, то получим функцию непрерывную на всей числовой оси. Математически это записывается как
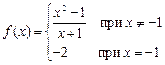
В общем случае, если  - точка разрыва функции
- точка разрыва функции 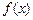 , но возможно найти для нее в точке
, но возможно найти для нее в точке  такое значение А, при котором измененная функция
такое значение А, при котором измененная функция 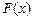 станет непрерывной, то это число А называется пределом функции
станет непрерывной, то это число А называется пределом функции 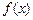 в точке
в точке  , а точка
, а точка  - точкой устранимого разрыва.
- точкой устранимого разрыва.
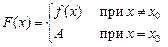
Математически это записывается формулой:
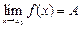
Существование предела функции 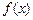 в точке
в точке  означает, что функция
означает, что функция 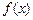 приближенно равна
приближенно равна 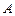 для всех значений
для всех значений 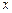 , близких к
, близких к  .
.
Определение. Постоянное число А называется пределом функции f(x) при 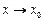 , если, задав произвольное как угодно малое положительное число e, можно найти такое d >0 (зависящее от e), что для всех x, лежащих в d - окрестности числа
, если, задав произвольное как угодно малое положительное число e, можно найти такое d >0 (зависящее от e), что для всех x, лежащих в d - окрестности числа  , т.е. для x, удовлетворяющих неравенству
, т.е. для x, удовлетворяющих неравенству 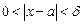 , значения функции f(x) будут лежать в e - окрестности числа А, т.е.
, значения функции f(x) будут лежать в e - окрестности числа А, т.е. 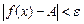 .
.
Это определение называют определением предела функции по Коши, или “на языке e - d“.
На рисунке 2.2. проиллюстрировано определение предела функции 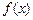 при
при 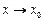 . Для построения этого рисунка необходимо выполнить следующие действия:
. Для построения этого рисунка необходимо выполнить следующие действия:
1. построить график функции 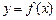 и отметить точки
и отметить точки  и А;
и А;
2. построить окрестность точки А, выбрав произвольное число 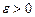 ;
;
3. по точкам 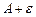 ,
, 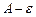 и графику функции построить
и графику функции построить 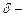 окрестность точки
окрестность точки  . Расстояния от точки
. Расстояния от точки  до точек
до точек 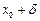 и
и 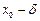 должны быть равными, поэтому из двух полученных отрезков следует взять меньший и отложить его в обе стороны от точки
должны быть равными, поэтому из двух полученных отрезков следует взять меньший и отложить его в обе стороны от точки  ;
;
4. взять произвольную точку 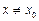 , принадлежащую окрестности точки
, принадлежащую окрестности точки  , и по графику функции найти значение
, и по графику функции найти значение 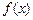 , которое должно попасть в построенную окрестность точки А.
, которое должно попасть в построенную окрестность точки А.
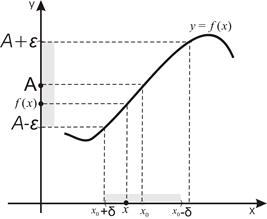 Рисунок 2.2 – Определение предела функции Рисунок 2.2 – Определение предела функции |
Если 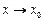 и при этом
и при этом 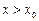 , то пишут
, то пишут 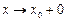 . Если, в частности,
. Если, в частности, 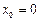 , то вместо символа 0+0 пишут +0.
, то вместо символа 0+0 пишут +0.
Аналогично если 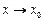 и при этом
и при этом 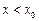 , то пишут
, то пишут 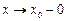 .
.
Числа 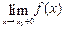 и
и 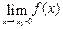 называются соответственно пределом справа и пределом слева функции f(x) в точке
называются соответственно пределом справа и пределом слева функции f(x) в точке  .
.
Для существования предела функции f(x) при 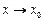 необходимо и достаточно, чтобы
необходимо и достаточно, чтобы 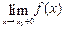 =
= 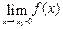 .
.
Определение. Переменная величина (т.е. последовательность или функция), имеющая своим пределом ноль, называется бесконечно малой величиной.
Определение. Переменная величина, имеющая бесконечный предел, называется бесконечно большой величиной.
