Практическое занятие. решение задач динамического программирования

Оптимизация решения о капиталовложениях в несколько объектов единовременно

Допустим, имеется возможность вложения средств С в группу из n предприятий на реконструкцию и модернизацию оборудования. Известен возможный прирост продукции на каждом предприятии в зависимости от выделенных ему средств r_i(x); .

Необходимо таким образом распределить инвестиции С между предприятиями, чтобы общий прирост выпуска продукции на всех n предприятиях в сумме был максимальным.

Составим основное функциональное уравнение. Обозначим через f₁ – максимально возможный прирост выпуска продукции на одном предприятии при различных значениях вкладываемых средств х. Каждому значению х отвечает определённый результат r₁(x):

где y_n-1 – допустимая сумма средств, которая может быть вложена в одно предприятие – это допустимое состояние процесса на начало первого шага вычислений.

На следующем шаге - оптимальный эффект от вложения средств в два предприятия получаем максимизируя объём прироста продукции на втором предприятии r₂(x) плюс оптимальный результат, полученный на предыдущем шаге:

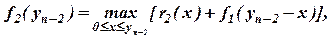
где y_n-2 – средства, вкладываемые в два предприятия;

х – средства, выделяемые второму предприятию;

(y_n-2 – x) – средства, вкладываемые в первое предприятие.

В общем случае функциональное уравнение задачи, позволяющее максимизировать эффект, получаемый на i-м шаге, плюс оптимальное решение, полученное на предыдущем шаге, имеет вид:

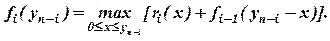
Задача. Составить оптимальный план распределения капиталовложений между четырьмя предприятиями (проектами) в размере С = 100 млн. ден. ед.

Объём капиталовложений млн. ден. ед.	Прирост выпуска продукции ri(xi) в зависимости от объёма капиталовложений, млн. ден. ед.
Проект 1	Проект 2	Проект 3	Проект 4

На первом этапе решения задачи динамического программирования, рассмотрим программу вложения средств в предприятие по шагам. На первом шаге максимизируем отдачу f₁(C) от вложения средств x₁ в одно (первое) предприятие:

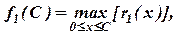
Отдача от средств, вкладываемых в 1-ое предприятие

С \ х							f1(C)	x1
			–	–	–	–
				–	–	–
					–	–
						–

На втором шаге максимизируем отдачу f₂(C) от вложения средств в два предприятия, из которых x₂ вкладывается во второе предприятие, с учётом результата, полученного на предыдущем шаге:

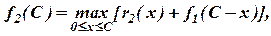
Отдача от средств, вкладываемых во 2-ое предприятие и их остатков, вкладываемых в 1-ое предприятие

С \ х							f2(C)	x2
	0+12	14+0	–	–	–	–
	0+33	14+12	28+0	–	–	–
	0+44	14+33	28+12	38+0	–	–
	0+64	14+44	28+33	38+12	56+0	–
	0+78	14+64	28+44	38+33	56+12	80+0

На третьем шаге максимизируем отдачу f₃(C) от вложения средств в три предприятия, из которых x₃ вкладывается в третье предприятие, с учётом результата, полученного на предыдущем шаге:

Отдача от средств, вкладываемых в 3-е предприятие и их остатков, вкладываемых в 1-ое и 2-ое предприятия

С \ х							f3(C)	x3
	0+14	13+0	–	–	–	–
	0+33	13+14	38+0	–	–	–
	0+47	13+33	38+14	47+0	–	–
	0+64	13+48	38+33	47+14	64+0	–
	0+80	13+64	38+47	47+33	64+14	79+0

На четвёртом шаге максимизируем отдачу f₄(C) от вложения средств в четыре предприятия, из которых x₄ вкладывается в четвёртое предприятие, с учётом результата, полученного на предыдущем шаге:

Отдача от средств, вкладываемых в 4-ое предприятие и их остатков, вкладываемых в 1-ое, 2-ое и 3-е предприятия

С \ х							f4(C)	x4
	0+14	18+0	–	–	–	–
	0+38	18+14	39+0	–	–	–
	0+52	18+38	39+14	48+0	–	–
	0+71	18+52	39+38	48+14	65+0	–
	0+85	18+71	39+52	48+38	65+14	82+0

На втором этапе решения задачи динамического программирования, проанализируем таблицы в обратном порядке. Максимальный прирост отдачи от вложения средств в размере 100 млн. ден. ед. на четырёх предприятиях составит 91 млн. ден. ед. (табл. 5). При этом в 4-ое предприятие следует вложить х₄ = 40 млн. ден. ед. Остаток средств 100 – 40 = 60 млн. ден. ед. вкладывают в развитие 1-го, 2-го и 3-го предприятий. Из табл. 4 видно, что из этой суммы в 3-е предприятие следует вложить х₃ = 40 млн. ден. ед. Остаток средств - 60 – 40 = 20 млн. ден. ед. вкладывают в развитие 1-го и 2-го предприятий. Из табл. 3 видно, что из этой суммы во 2-е предприятие следует вложить всю оставшуюся сумму х₂ = 20 млн. ден. ед. Вложение средств в 1-ое предприятие нерентабельно.

f = 91, x₁ = 0, x₂ = 20, x₃ = 40, x₄ = 40.

Решение задач динамического программирования

Оптимизация решения о капиталовложениях в течение нескольких временных периодов

Задача 1. Допустим, имеется возможность финансирования двух проектов в объеме 100 ден. ед. (Z₁=100 ден. ед). Если в 1-й проект вложить Х ден.ед., то доход от этого проекта будет определяться функцией f(X)=4X. Если во 2-й проект вложить Y ден.ед., то доход от этого проекта будет определяться функцией g(Y)=3Y. Уменьшение остатка средств после вложения в 1-й и 2-й проекты происходит в соответствии с законами: φ(X)=0,2Х (для первого проекта) и Ψ(Y)=0,6Y (для второго проекта).

Нужно распределить данные средства в течение 3 лет таким образом, чтобы общий доход за 3 года был максимальным.

Решение. Решаем задачу с конца.

1 шаг. Планируем распределение средств на 3-й год. Предположим, что общий остаток средств после второго года – к началу 3-го года равна Z₃. Распределим их между проектами.

Если в 1-й проект вложить Х₃ ден. ед., тогда во 2-й проект останется вложить Y₃=Z₃ – X₃. Тогда доход за 3-й год от 1-го проекта составит f(X₃)=4·X₃, а от 2-го проекта g(Y₃)=3(Z₃ – X₃).

Z3	1 проект	2 проект
вложения	Х3	Y3=Z3 – X3
доход	f(X3)=4 X3	g(Y3)=3(Z3 – X3).

Тогда суммарный доход за 3-й год составит

F₃=4 X₃ +3Z₃ – 3X₃ = X₃ +3Z₃

Необходимо найти максимум этой функции дохода при условии, что 0≤X₃≤Z₃. Уравнение F₃= X₃ +3Z₃ линейно относительно X₃. Значит, максимальное значение лежит на границах интервала.

Максимум достигается в точке X₃ = Z₃, т.е. для максимизации дохода необходимо в 3-м (последнем) году направить все оставшиеся средства на 1-й проект.

мах. доход F₃^*=4 Z₃

2 шаг. Начало 2-го года планирования к началу 2-го года функционирования системы в нашем распоряжении средства в количестве Z₂. (Остаток после 1-го года).

Если в 1-й проект вложить Х₂ ден. ед., тогда во 2-й проект останется вложить Y₂=Z₂ – X₂.

Z2	1 проект	2 проект
вложения	Х2	Y2=Z2 – X2
доход	f(X2)= 4 X2	g(Y2)=3Y2=3(Z2 – X2).

Тогда суммарный доход за 2 последние года составит

F_2,3=4 X₂ +3Z₂ – 3X₂ + 4Z₃,

но Z₃ – это остаток средств после 2-го года, который можно выразить через φ(X₂)=0,2Х₂ и Ψ(Y₂)=0,6 Y₂

Z₃ = 0,2X₂ + 0,6Y₂ = 0,2 X₂ + 0,6 (Z₂ – X₂) = 0,6 Z₂ - 0,4 X₂

F_2,3=4 X₂ +3Z₂ – 3X₂ + 4 (0,6 Z₂ - 0,4 X₂) = 5,4 Z₂ - 0,6 X₂

Найти максимум этой функции дохода при условии, что 0≤X₂≤Z₂.

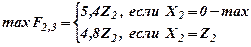
Значит, в начале 2-го года все средства надо вложить в 1 проект, в результате максимальный доход F_2,3^*= 5,4 Z₂

3 шаг. Начало 1-го года. К началу 1-го года в нашем распоряжении средства в количестве Z₁.

1-й проект получает Х₁ ден. ед., 2-й - Y₁=Z₁ – X₁.

Z1	1 проект	2 проект
вложения	Х1	Y1=Z1 – X1
доход	f(X2)= 4 X1	g(Y1)=3Y1=3(Z1 – X1).

Cуммарный доход за 3 года составит

F_1,2,3=4 X₁ +3(Z₁ – X₁) + 5,4Z₂,

но Z₂ – это остаток средств после 1-го года

Z₂ = 0,2X₁ + 0,6Y₁ = 0,2 X₁ + 0,6 (Z₁ – X₁) = 0,6 Z₁ - 0,4 X₁

F_1,2,3= X₁ +3Z₁ + 5,4 (0,6 Z₁ - 0,4 X₁) = 6,24 Z₁ - 1,16 X₁

Найти максимум этой функции дохода при условии, что 0≤X₁≤Z₁.

Все средства вкладываем во 2 проект, в результате максимальный доход F_1,2,3^*= 6,24 Z₁ = 6,24 * 100 = 624 ден. ед.

Оптимальное управление состоит в том, что в первые два года все средства нужно вложить во 2-й проект и только в 3-м году все средства нужно отдать 1-му проекту. Тогда доход будет максимальным.

2 этап.

Вложения в проекты
	I	II	Доход	Остаток
1 год	Х1*=0	Y1*=100	F1=g(Y1)=100*3=300	Z2=Ψ(Y2)=0,6*Y=60
2 год	Х2*=0	Y2*=60	F2=g(Y2)=60*3=180	Z3=Ψ(Y3)=0,6*Y=36
3 год	Х3*=36	Y3*=0	F3=f(X3)=36*4=144	F1+F2+F3=624

Задачи об использовании и замене оборудования

Общая постановка

Для осуществления своей деятельности предприятия время от времени должно производить замену своего оборудования. При замене оборудования учитывается:

1) производительность используемого оборудования;

2) затраты на ремонт и содержание оборудования;

3) стоимость приобретенного и заменяемого оборудования.

Предположим, что к началу планируемого периода на предприятии установлено новое оборудование, позволяющее за каждый τ-й год выпустить готовой продукции на сумму R(τ) рублей, а ежегодные затраты, связанные с ремонтом и содержанием оборудования равны Z(τ) рублей.

В τ-й год оборудование может быть продано за S(τ) рублей, а новое куплено за С рублей. С учетом всех этих факторов найти план замены оборудования, обеспечивающий максимальную прибыль за N лет.

3адача. На предприятии установлено новое оборудование. Зависимость производительности его от времени использования, а также зависимость затрат на содержание и ремонт при различном времени использования приведены в табл. 1.

Таблица 1

	Время, в течении которого используется оборудование (τ)
Годовой выпуск продукции R(τ), т.руб.
Ежегодные затраты на ремонт и содержание оборудования Z(τ), т.руб.

Зная затраты, связанные с приобретением и установкой нового оборудования (идентичного старому оборудованию), которые составляют 40 тыс.р. и то, что заменяемое оборудование списывается, составить такой план замены оборудования в течении 5 лет, при котором общая прибыль (полезный эффект) за весь период была бы максимальной

Решение

Обозначим через u₁ – решение сохранить (оставить) старое оборудование, а через u₂ – решение о замене оборудования.

1-й этап. Начинаем от начала 5-го года. Для того, чтобы найти условно-оптимальное управление составим уравнение Беллмана.

Мы предполагаем, что к концу k-го года (k=1..5) может применяться одно из 2 решений: либо сохранить, либо заменить оборудование. Исходя из этого прибыль предприятия за k-й год можем записать следующим образом:

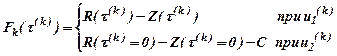
где τ^(k) – возраст оборудования к началу k-го года,

u^(k) – управление, реализуемое к началу k-го года,

С – стоимость нового оборудования.

Уравнение Беллмана выглядит следующим образом:

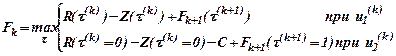(12)

это прибыль за k лет.

Используя уравнение (1) начнем с определения условно-оптимального управления для последнего 5-го года.

Для этого находим множество допустимых состояний оборудования к началу данного года.

Т.к. к началу первого года пятилетки имеется новое оборудование, а это означает что τ⁽¹⁾ =0, то возраст оборудования к началу 5-го года может быть 1,2,3,4 года.

Поэтому допустимые состояния на данный период таковы: к началу 5 года:

τ₁⁽⁵⁾ =1; τ₂⁽⁵⁾ =2; τ₃⁽⁵⁾ =3; τ₄⁽⁵⁾ =4.

Для каждого из этих состояний найдем условно-оптимальное управление, и соответствующие значения прибыли (полезного эффекта) F₅(τ⁽⁵⁾).

Используя уравнение (12) и соотношение F₆(τ⁽⁶⁾)=0, получим следующее значение прибыли:

(13)

Подставляя в (13) все значения τ⁽⁵⁾ и учитывая данные табл. 1, получим:

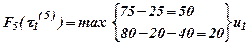, т.к. max достигается при управлении u₁.

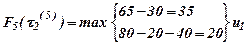
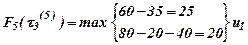
. Запишем данные в табл. 2.

Таблица 2

τ(5) -год	F5(τ(5)) – функция цели	u*- решение
		u1
		u1
		u1
		u2

Подходим к началу 4-го года τ₁⁽⁴⁾ =1; τ₂⁽⁴⁾ =2; τ₃⁽⁴⁾ =3.

Подставляя в (13) все значения τ⁽⁵⁾ и учитывая данные табл. 1, получим:

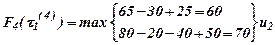
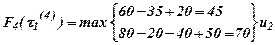
Таблица 3

τ(4) -год	F4(τ(4)) – функция цели	u*- решение
		u1
		u2
		u2

Подходим к началу 3-го года τ₁⁽³⁾ =1; τ₂⁽³⁾ =2.

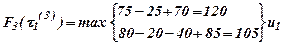
Таблица 4

τ(3) -год	F3(τ(3)) – функция цели	u*- решение
		u1
		u2

Подходим к началу 2-го года τ₁⁽²⁾ =1.

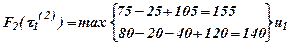
Таблица 5

τ(3) -год	F3(τ(3)) – функция цели	u*- решение
		u1

Согласно условию к началу 1-го года состояние оборудования τ⁽¹⁾ =0, поэтому проблемы выбора нет и оборудование сохраняют.

F₁(τ⁽¹⁾)=80-20-40+155=175 - условно-оптимальное решение.

Это максимальная прибыль соответствует оптимальному плану замены оборудования, которая получается на основе данных всех таблиц и в результате реализации 2-го этапа.

1-й год – решение единственное – оборудование сохранить. К началу 2-го оборудованию будет 1 год. Тогда в соответствии с данными табл. 5 оптимальным решением 2-го года будет решение тоже сохранить оборудование. Реализация такого решения приводит к тому, что возраст оборудования к началу 3-го года будет 2 года. Тогда в 3-м году оптимальное решение поменять оборудование (табл. 4). После замены оборудования его возраст к началу 4-го года равен 1 году. Из табл. 3 видно, что оборудование менять не следует. Поэтому к началу 5 года возраст оборудования будет 2 года и менять его не надо (табл. 2).

Таким образом, оптимальный план замены оборудования:

1 год –сохранять, 2- сохранять, 3 – заменить, 4 – сохранять,

5 – сохранять.