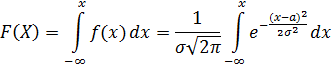Непрерывная случайная величина. функция распределения. плотность вероятности. вероятность попадания в заданный интервал

Непрерывной случайной величиной называют случайную величину, значения которой сплошь заполняют некоторый интервал.

Например, рост человека ‒ непрерывная случайная величина.

Функцией распределения случайной величины называют вероятность того, что случайная величина Х принимает значения, меньшие х.

F (x) = P ( X

Геометрически, формула F(x) = P (X означает, что все значения Х будут находиться, левее х. Функция F(x) называется интегральной функцией.

Плотностью вероятности непрерывной случайной величины f (x) называется производная от функции распределения этой случайной величины:

Следовательно, F(x) первообразная для f (x).

Теорема. Вероятность попадания непрерывной случайной величины X в интервал от a до b находится по формуле:

Доказательство.

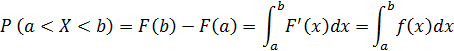
Следствие. Если все возможные значения случайной величины

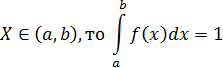
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ И ДИСПЕРСИЯ НЕПРЕРЫВНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ

1. Математическое ожидание:

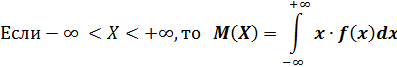
2. Дисперсия:

Преобразуем эту формулу:

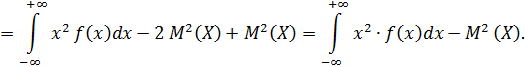
‒ формула дисперсии для непрерывных случайных величин.

Тогда среднее квадратическое отклонение:

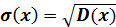
ОСНОВНЫЕ ЗАКОНЫ РАСПРЕДЕЛЕНИЯ НЕПРЕРЫВНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН.

Нормальный закон распределения.

Из всех законов распределения для непрерывных случайных величин на практике чаще всего встречается нормальный закон распределения. Этот закон распределения является предельным, то есть все остальные распределения стремятся к нормальному.

Теорема 1.Непрерывная случайная величина распределена по нормальному закону с параметрами а и ,если плотность вероятности имеет вид:

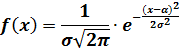
Математическое ожидание случайной величины, распределённой по нормальному закону распределения, равно а, то есть 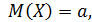дисперсия .

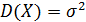Теорема 2.Вероятность попадания непрерывной случайной величины, распределенной по нормальному закону распределения в интервал от α до β, находится по формуле:

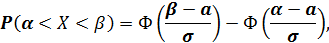
Пример.

Полагая, что рост мужчин определенной возрастной группы есть нормально распределенная случайная величина X, c параметрами а = 173 и = 36.

Найти:
а) выражение плотности вероятностей и функции распределения случайной величины X;

б) долю костюмов 4-го роста (176 – 182 см) в общем объеме производства.

Решение:

Плотность вероятности нормально распределенной случайной величины:

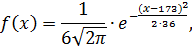
Доля костюмов 4-го роста (176 – 182 см.) в общем объеме производства определяется по формуле как вероятность

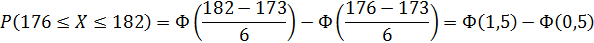
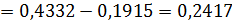
0,2417 100% 24,2% ‒ доля костюмов 4-го роста в общем объеме производства.

Итак, функция плотности вероятностей нормального закона распределения имеет вид:

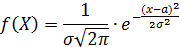
Тогда функция распределения: