Производная частного функций
В потолке открылся люк, не пугайся, это глюк.
А вот это вот суровая действительность:
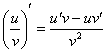
Пример 8
Найти производную функции 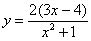
Чего здесь только нет – сумма, разность, произведение, дробь…. С чего бы начать?! Есть сомнения, нет сомнений, но, В ЛЮБОМ СЛУЧАЕ для начала рисуем скобочки и справа вверху ставим штрих:
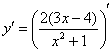
Теперь смотрим на выражение в скобках, как бы его упростить? В данном случае замечаем множитель, который согласно первому правилу целесообразно вынести за знак производной:
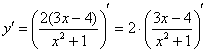
Заодно избавляемся от скобок в числителе, которые теперь не нужны.
Вообще говоря, постоянные множители при нахождении производной можно и не выносить, но в этом случае они будут «путаться под ногами», что загромождает и затрудняет решение.
Смотрим на наше выражение в скобках. У нас есть сложение, вычитание и деление. Со школы мы помним, что деление выполняется в первую очередь. И здесь – сначала применяем правило дифференцирования частного:

Таким образом, наша страшная производная свелась к производным двух простых выражений. Применяем первое и второе правило, здесь это сделаем устно, надеюсь, Вы уже немного освоились в производных:
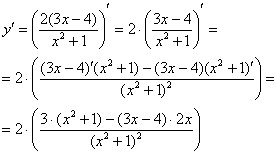
Штрихов больше нет, задание выполнено.
На практике обычно (но не всегда) ответ упрощают «школьными» методами:

Пример 9
Найти производную функции 
Это пример для самостоятельного решения (ответ в конце урока).
Время от времени встречаются хитрые задачки:
Пример 10
Найти производную функции 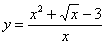
Смотрим на данную функцию. Здесь снова дробь. Однако перед тем как использовать правило дифференцирования частного (а его можно использовать), всегда имеет смысл посмотреть, а нельзя ли упростить саму дробь, или вообще избавиться от нее?
Дело в том, что формула 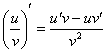 достаточно громоздка, и применять ее совсем не хочется.
достаточно громоздка, и применять ее совсем не хочется.
В данном случае можно почленно поделить числитель на знаменатель.
Преобразуем функцию:

Ну вот, совсем другое дело, теперь дифференцировать просто и приятно:

Готово.
Пример 11
Найти производную функции 
Здесь ситуация похожа, превратим нашу дробь в произведение, для этого поднимем экспоненту в числитель, сменив у показателя знак:

Произведение все-таки дифференцировать проще:
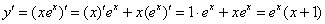
Пример 12
Найти производную функции 
Это пример для самостоятельного решения (ответ в конце урока).
Решения и ответы:
Пример 4: 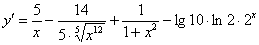 . В ходе решения данного примера следует обратить внимание, на тот факт, что
. В ходе решения данного примера следует обратить внимание, на тот факт, что  и
и 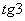 – постоянные числа, не важно чему они равны, важно, что это - константы. Поэтому
– постоянные числа, не важно чему они равны, важно, что это - константы. Поэтому  выносится за знак производной, а
выносится за знак производной, а 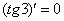 .
.
Пример 7: 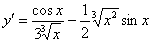
Пример 9: 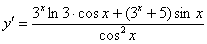
Пример 12: 
