Аксиома непрерывности Кантора
16. Пусть элементы x 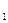 ,x
,x 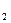 ,…,x
,…,x 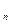 ,…,y
,…,y 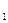 ,y
,y 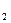 ,…,y
,…,y 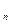 ,… удовлетворяют условию x
,… удовлетворяют условию x 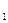 <x
<x 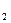 <…<x
<…<x 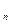 <…<y
<…<y 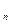 <…y
<…y 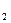 <y
<y 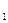 и пусть для любого положительного элемента e>0, начиная с некоторого номера n, выполняются условия y
и пусть для любого положительного элемента e>0, начиная с некоторого номера n, выполняются условия y 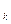 -x
-x 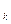 < e, k = n, n+1, … . Тогда существует элемент Z такой, что при всех значениях n выполняется x
< e, k = n, n+1, … . Тогда существует элемент Z такой, что при всех значениях n выполняется x 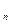 < Z < y
< Z < y 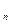 .
.
То, что элемент Z, о котором говорится в этой аксиоме, является единственным, несложно доказать от противного.
Определение 2.
Множество R называется множеством действительных чисел, а его элементы действительными числами, если они удовлетворяют всем тем же аксиомам 1-15, что и рациональные числа и, дополнительно, аксиом непрерывности Кантора.
О представлении действительных чисел.
Мы видели, что формирование аксиоматик множеств натуральных рациональных и действительных чисел связано с выполнением определенных операций над числами. Система записи или представления чисел связана и с другими задачами.
Задача 1.
Построить символьную запись числа, в которой эффективно реализуются алгоритмы арифметических и алгебраических операций. Мы уже отмечали, что наиболее подходящей для этой цели является систематическая запись числа (десятичная, двоичная и др.)
Задача 2.
Построить представление чисел, в котором иррациональные числа приближаются рациональными числами наилучшим образом. Рациональная дробь p/q приближает иррациональное число a наилучшим образом, если для любого рационального числа m/n с n£q выполняется равенство |a-p/q| < |a-m/n|.
Рассмотрим десятичные приближения. Пусть m = a 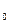 , a
, a 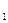 , …,a
, …,a 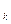 - десятичное приближение с “k” знаками после запятой числа a = a
- десятичное приближение с “k” знаками после запятой числа a = a 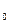 , a
, a 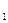 , …,a
, …,a 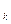 ,a
,a 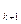 ,… . Тогда погрешность этого измерения определяется разностью:
,… . Тогда погрешность этого измерения определяется разностью:
|a-m/n| = a 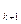 /10
/10 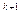 +a
+a 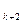 /10
/10 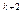 +…<9/10
+…<9/10 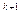 (1+1/10+…) = 9/10
(1+1/10+…) = 9/10 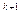 ´
´
1/(1-1/10) = 1/10 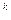 ~1/n.
~1/n.
Для более лучших приближений используется представление иррационального числа цепной дробью, [6]. Если p/q - конечная цепная дробь, приближающая число a, то [6], стр. 46, |a-p/q| < 1/q 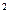 .
.
Таким образом, представление числа цепной дробью «более экономично», чем представление десятичной дробью.
Напомним, что до сих пор не найдены эффективные алгоритмы арифметических операций для представлений чисел в виде цепных дробей, [6], стр. 29-30.
Аксиоматическое обоснование евклидовой геометрии.
О “Началах” Евклида.
Александрийский ученый Евклид, живший в третьем веке до нашей эры, впервые в истории предпринял попытку глобальной систематизации математических фактов. Его “Начала” состояли из 13 книг, которые представляли собой, по существу, главы, посвященные отдельным вопросам математики. В них дано безупречное для того времени построение геометрии. Евклид начинал изложения с определений, постулатов и аксиом. Затем идут теоремы, которые представляют собой умозаключения, основанные на постулатах, аксиомах, определениях и ранее доказанных теоремах.
Математические построения начинаются с 23 определений. Приведем некоторые из них:
· Точка есть то, что не имеет частей;
· Линия же - длина без ширины;
· Концы линии - точки;
· Прямая линия есть та, которая равно расположена по отношению к точкам на ней;
· Параллельные прямые - это прямые которые находятся в одной плоскости и при неограниченном продолжении ни с той, ни с другой стороны не пересекаются и т.д.
Далее Евклид излагает постулаты и аксиомы, формулировки которых представляют для нас лишь исторический интерес.
Постулаты.
1. От всякой точки до всякой точки можно провести прямую линию.
2. Каждую прямую можно непрерывно продолжать по прямой.
3. Из любого центра можно описать окружность любым радиусом.
4. Все прямые углы равны между собой.
Если прямая, падающая на две прямые, образует внутренние по одну сторону углы, меньшие в сумме двух прямых, то продолженные эти прямые неограниченно встретятся с той стороны, где углы в сумме меньше двух прямых.
Аксиомы.
1. Равные одному и тому же равны между собой.
2. Если к равным прибавляются равные, то целые будут равны.
3. Если от равных отнимаются равные, то остатки будут равны.
4. Если к неравным прибавляются неравные, то целые будут не равны.
5. Удвоенные одного и того же равны между собой.
6. Половины одного и того же равны между собой.
7. Совмещающиеся друг с другом равны между собой.
8. Целое больше части.
9. Две прямые не содержат пространства.
Построения оснований геометрии были проделаны Евклидом с большим мастерством. “Начала” Евклида затмили сочинения его предшественников и на протяжении более чем двух тысяч лет “Начала” представляли образец математической строгости.
С точки зрения современной математики дедуктивные построения Евклида не отражают все отношения между геометрическими элементами, часть определений логически не задействована, а сами доказательства опираются на ряд неопределяемых понятий.
Существуют различные объяснения роли аксиом и постулатов в “Началах”. Постулаты играют роль модельной аксиоматики, а аксиомы “Начал” являются прообразом аксиоматики действительных чисел. На интуитивном уровне “Начала” предвосхищают многие математические построения.
