Основные теоремы и формулы
Введем обозначения:  - оригинал;
- оригинал; 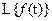 ,
,  - изображение.
- изображение.
1). Свойство линейности:
 , где
, где
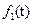 ,
,  - оригиналы,
- оригиналы,  ,
, 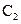 - константы
- константы
2). Теорема смещения:

3). Теорема интегрирования изображения:

4). Теорема дифференцированного изображения:
5). Теорема о дифференцировании оригинала:
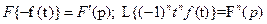
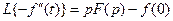 ;
; 
6).Основные формулы:
| № | Оригинал | Изображение |
 | ||
 | 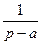 | |
 | 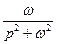 | |
 | 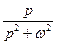 | |
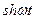 | 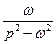 | |
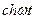 | 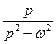 | |
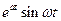 | 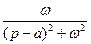 | |
 | 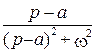 | |
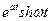 | 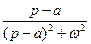 | |
 |  | |
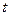 |  | |
 | 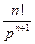 | |
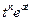 | 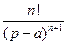 | |
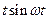 |  | |
 | 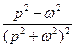 | |
 | 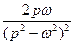 | |
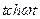 | 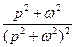 |
2. Определение изображения
2.1 Задачи
1)  | 2) 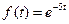 | 3) 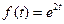 |
4) 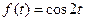 | 5)  | 6)  |
7) 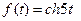 | 8)  | 9)  |
10) 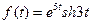 | 11) 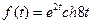 | 12) 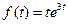 |
13) 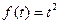 | 14) 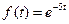 | 15) 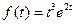 |
16)  | 17)  | 18) 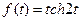 |
19) 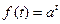 | 20) 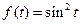 | 21) 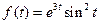 |
22)  | 23) 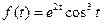 | 24)  |
25)  | 26) 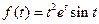 | 27) 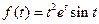 |
28) 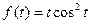 | 29)  | 30)  |
31) 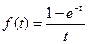 | 32)  |
2.2 Ответы
1) 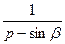 | 2) 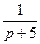 | 3)  |
4) 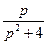 | 5)  | 6) 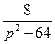 |
7)  | 8) 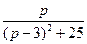 | 9) 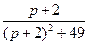 |
10) 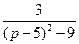 | 11)  | 12)  |
13)  | 14)  | 15)  |
16)  | 17) 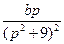 | 18)  |
19) 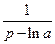 | 20)  | 21)  |
22) 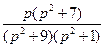 | 23) 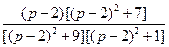 | 24) 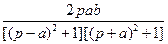 |
25) 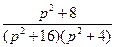 | 26)  | 27) 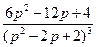 |
28)  | 29) 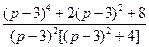 | 30)  |
31)  | 32)  |
2.3. Указания
1) См. ф2 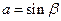 | 2) См. ф2 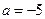 | 3) См. ф2 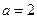 |
4) См. ф4 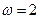 | 5) См. ф2 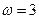 | 6) См. ф5  |
7) См. ф6  | 8) См. ф7 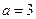 , ,  | 9) См. ф8 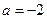 , ,  |
10) См. ф9 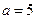 , , 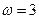 | 11) См. ф10 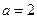 , ,  | 12) См. ф13  , , 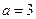 |
13) См. ф12  | 14) См. ф12 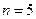 | 15) См. ф13 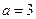 , , 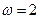 |
16) См. ф13  , , 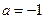 | 17) См. ф14 | 18) См. ф17 |
19) Представить  , ф. 2.
, ф. 2.
20) См. ф22 21) См. решение задачи 20+т.2(смещение)
22) Воспользоваться представлением cost в виде (19), возвести в куб, затем – таблица, ф-ла 2.
23) См. решение задачи 22+т.2(смещение)
24)Воспользоваться представлением  в виде (20), затем таблица, ф-ла 7
в виде (20), затем таблица, ф-ла 7
25)Представить 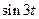 в виде (18),
в виде (18),  в виде (19)
в виде (19)
26)Первый способ: представить  в виде (18), затем - формула (13); второй способ: использовать т.4
в виде (18), затем - формула (13); второй способ: использовать т.4
27) См. решение задачи 26+т.2(смещения)
28) Использовать ф.23
29)см. решение задачи 28+т.2(смещения)
30)-32). Воспользоваться т.3 об интегрировании изображений.
2.4.Решения
20)  ,
, 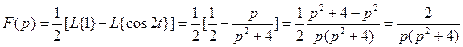
21) В ответ задачи 20 вместо p подставляем  , получаем
, получаем

22) 
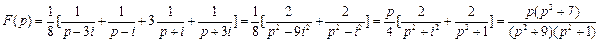
23) В ответ задачи 22 вместо p подставляем 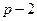 , получаем
, получаем
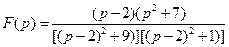
24) 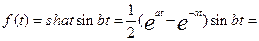
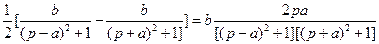
25) 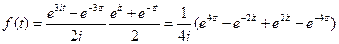

26) 
27) В ответе задачи 22 вместо p подставляем  , получим
, получим
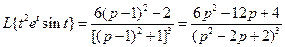
28) 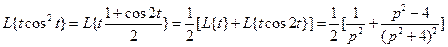
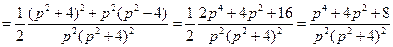
29) В ответе задачи 28 вместо p подставляем 

30) 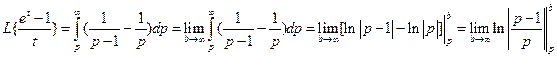
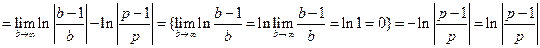
31) 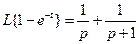

32) 
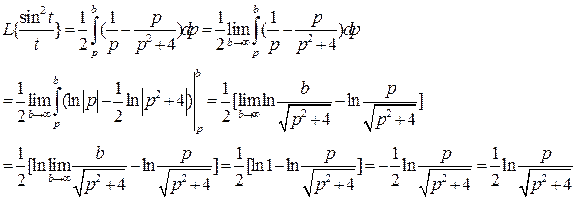
3. Определение оригинала
3.1. Задачи
33) 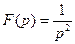 | 34) 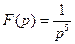 | 35)  |
36)  | 37) 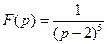 | 38) 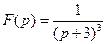 |
39) 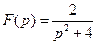 | 40) 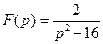 | 41)  |
42)  | 43)  | 44)  |
45) 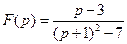 | 46) 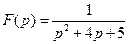 | 47)  |
48)  | 49)  | 50) 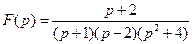 |
51) 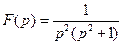 | 52)  | 53) 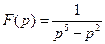 |
54) 
3.2.Ответы
33) 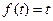 | 34)  |
35) 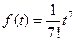 | 36) 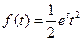 |
37) 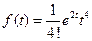 | 38)  |
39) 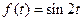 | 40)  |
41) 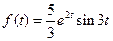 | 42)  |
43)  | 44) 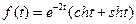 |
45)  | 46) 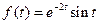 |
47)  | 48)  |
49)  | 50) 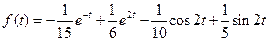 |
51)  | 52) 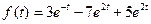 |
54) 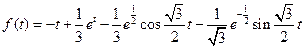 | 54)  |
3.3. Указания
| 33) См. ф.11 | 34) См. ф.12 | 35) См. ф.12 |
| 36) См. ф.13 | 37) См. ф.13 | 38) См. ф.13 |
| 39) См. ф.3 | 40) См. ф.5 | 41) См. ф.7 |
| 42) См. ф.4 | 43) См. ф.10 |
44)Представить числитель в виде 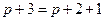 , разделить почленно числитель на знаменатель, затем использовать формулы 9,10
, разделить почленно числитель на знаменатель, затем использовать формулы 9,10
45) Представить числитель в виде 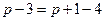 ,см. указание 44
,см. указание 44
46)-49) Выделить полный квадрат в знаменателе и свести к использованию формул 7, 9 или 8,10.
50)-53) Необходимо разложить данные в условии рациональные дроби вычисляется как сумма оригиналов соответствующих простейших дробей
50) 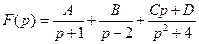
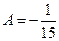
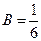
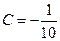
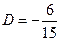
51) 
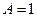 ,
,  ,
, 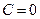 ,
, 
52) 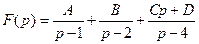
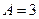 ,
,  ,
, 
53) 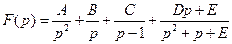
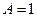 ,
,  ,
,  ,
,  ,
, 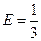
54) Разложить на множители знаменатель и преобразовать дробь
3.4. Решение
33) 
34) 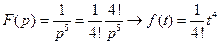
35) 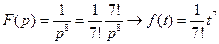
36) 
37) 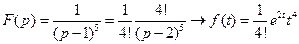
38) 
39) См.указание 39
40) 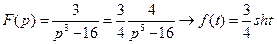
41) 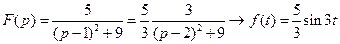
42) См.указание 42
43) См.указание 42
44) 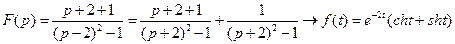
45) 

46) 
47) 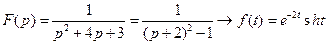
48) 
См.ф.8,7; 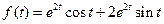
49) 
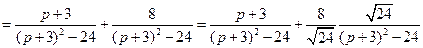
См.ф.9,10; 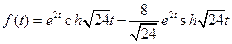
50) 
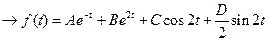
Найдем коэффициенты 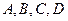

При 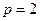

При 

При 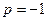
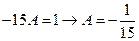
Сравнивая коэффициенты при 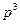 , получаем
, получаем

51) 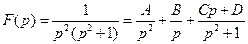
Найдем коэффициенты А,В,C,D
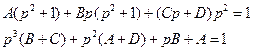
Сравнивая коэффициенты при 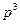 ,
, 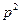 , p,
, p, 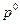 , получаем
, получаем
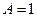

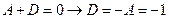
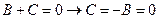
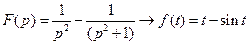
52)

При 
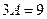
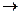
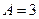
При 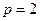

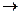

При 
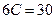
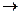

53) 

При 
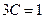
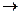 С=
С= 
При 
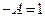
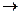
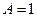
Перепишем предыдущее равенство в виде
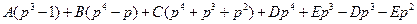
Сравнивая коэффициенты при 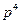 ,
, 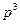 ,
, 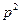 , получаем систему
, получаем систему
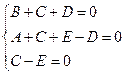
из которой найдем  ,
,  ,
, 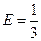
Итак, 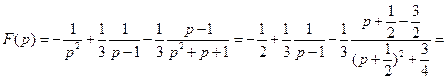
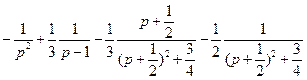
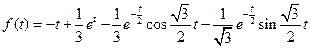
54) 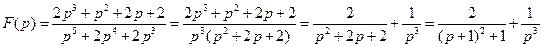

4. Решение дифференциальных уравнений
4.1 Задачи
Найти частное решение дифференциальных уравнений и систем, соответствующее заданным начальным условиям
55. 
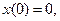

56. 

56. 
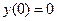 .
. 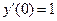
57. 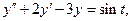
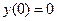 ,
, 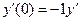
58. 

59. 
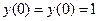
60. 
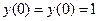
61. 
 62.
62. 
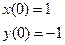
63. 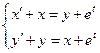
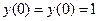
4.1. Ответы
55.  56.
56. 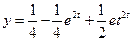
57. 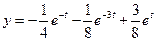 58.
58. 
59.  60.
60. 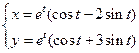
61.  62.
62. 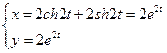
63. 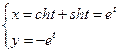 64.
64. 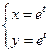
4.3. Указания
Введем обозначения: 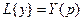 ,
,  Из теоремы 5 о дифференцировании оригинала следует:
Из теоремы 5 о дифференцировании оригинала следует:
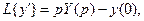



55) - 59). Применим к обеим частям уравнения теорему о дифференцировании оригинала (формулы (24)) и свойство линейности преобразования Лапласа. Вместо исходного дифференциального уравнения с начальными условиями получаем так называемое -изображающее уравнение. Последнее всегда является линейным алгебраическим уравнением относительно изображения неизвестной функции
60) -64). Решение системы линейных дифференциальных уравнений с постоянными коэффициентами операционным методом проводится по той же схеме, что и решение одного дифференциального уравнения. Применяя преобразование Лапласа к обеим частям каждого уравнения, используя формулы (24) и свойство линейности преобразования Лапласа, получаем так называемую изображающую систему, которая является линейной алгебраической системой относительно X и Y. Для определения X и Y здесь можно использовать правило Крамера:
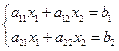

Если 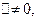 то
то  ,
, 
4.4. Решения
5.5. 

Учитывая заданные начальные условия, получаем
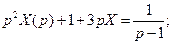

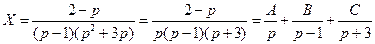
Следовательно, 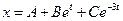
Найдем постоянные 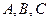 . Приравнивая числители после приведения к общему знаменателю в выражении для
. Приравнивая числители после приведения к общему знаменателю в выражении для 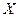 , получим
, получим

Полагая  , получим
, получим 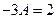
 . Аналогично при
. Аналогично при  имеем
имеем 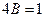
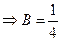 ; и при
; и при  получаем С=
получаем С=  . Таким образом,
. Таким образом, 
2). 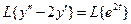 ;
; 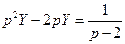

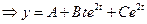
Найдем постоянные 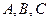 :
:  Отсюда, если p=0, то
Отсюда, если p=0, то 
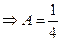 . p=2
. p=2  . Приравниваем коэффициенты при
. Приравниваем коэффициенты при 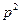 в правой и левой частях равенства, получим
в правой и левой частях равенства, получим
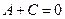
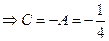 . Тогда
. Тогда 
3.) 
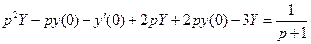
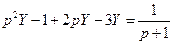 ,
, 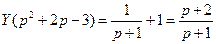
Отсюда
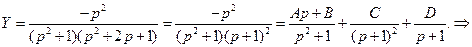
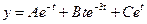
Найдем постоянные 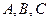 . Имеем
. Имеем
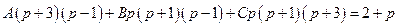 . Отсюда
. Отсюда
при  :
: 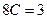

при  :
: 
при 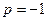 :
: 
4.) 
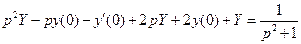
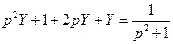
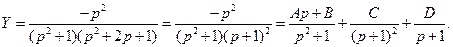
 ,
,
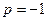
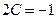
 ,
, 

Приравниваем коэффициенты при 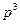 и
и 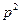 в обеих частях равенства, получим еще два уравнения
в обеих частях равенства, получим еще два уравнения
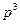 :
: 
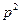 :
: 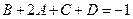 .
.
В итоге 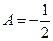 ,
,  ,
, 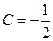 ,
, 
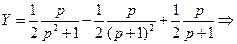
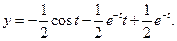
5). 

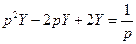
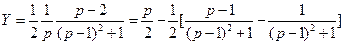 .
.

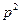 :
: 
 :
: 
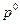 :
: 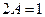 . Итак,
. Итак, 
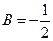 ,
, 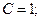


6). 
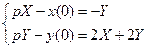
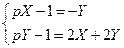

Получили линейную систему с постоянными коэффициентами относительно неизвестных 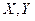 :
:
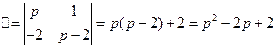


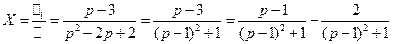
Отсюда x= 
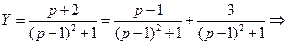
y= 
7). 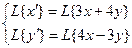

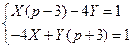

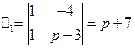
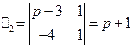
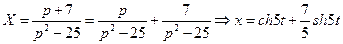
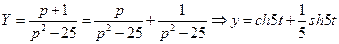
8). 
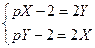

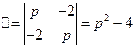
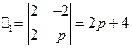

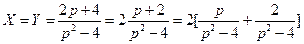
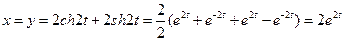
9). 
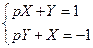

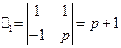



10). 





Итак, 

