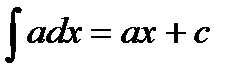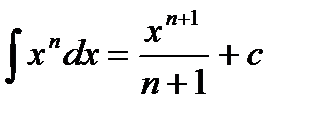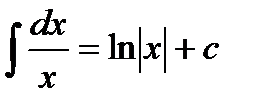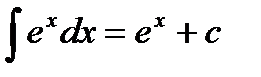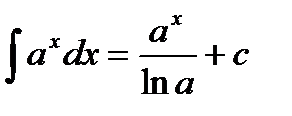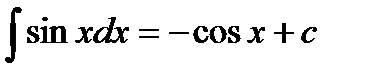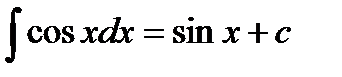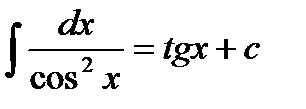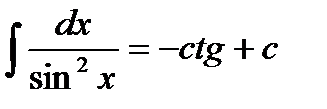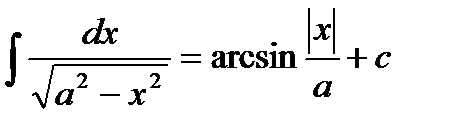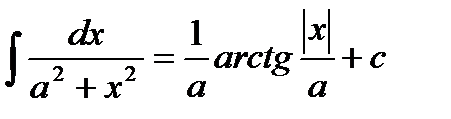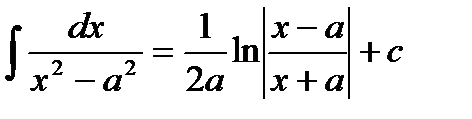Специальности 2 - 27 01 01

ЗАДАНИЯ ДЛЯ КОНТРОЛЬНОЙ РАБОТЫ

ДЛЯ УЧАЩИХСЯ ЗАОЧНОЙ ФОРМЫ ОБУЧЕНИЯ

СПЕЦИАЛЬНОСТИ 2 - 27 01 01

«ЭКОНОМИКА И ОРГАНИЗАЦИЯ ПРОИЗВОДСТВА»

М и н с к 2015

Автор: Толок Елена Ивановна, преподаватель УО «Минский государственный торговый колледж»

Рецензент(ы)

(Ф.И.О., должность, наименование организации, учреждения образования)

Разработано на основании индивидуальной учебной программы дисциплины

«Математика»,

утвержденной ______________________________________________________

(кем,когда)

Обсуждено и одобрено на заседании предметной (цикловой) комиссии

___________________________________________________________________

(наименование предметной (цикловой) комиссии)

Протокол№__________ от «____»________________2015г. _________________

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА.

Научно-технический прогресс невозможен без развития фундаментальных наук, среди которых математика занимает особое место. Математическое моделирование явлений природы и процессов, происходящих в обществе, сегодня широко используется в различных областях трудовой и творческой деятельности человека. Применение ЭВМ существенно расширяет класс теоретических и практических задач, посторонние и детальный анализ их математических моделей.

В последнее время значительно возросло примечание математических методов при решении проблемы экономики. Абстрактные понятия математики позволяют создавать и изучать математические модели вполне определенных процессов и различных сферах экономической деятельности. Большинство важнейших понятий экономики – бюджетные линии, спрос, предложение, цена равновесия, эластичность, предельная полезность и т.д. – являются, по существу, конкретными примерами понятий математического анализа: функция, предел функции, производная, логарифмическая производная т.п.

Компьютеризация общества, внедрение современных информационных технологий требуют математической грамотности специалиста буквально на каждом рабочем месте. Это предполагает и конкретные математические знания, и определенный стиль мышления, вырабатываемые в процессе изучения математики. Специальности экономического профиля требуют высокого уровня обязанности и связаны с непосредственным применением математики. В связи с этим повышается роль математики в подготовке кадров со средним специальным образованием в области экономики, бизнеса, маркетинга и управления.

Программой предусматривается изучение разделов высшей математики, которые находят широкое применение, как в теории специальных предметов, так и в практической работе специалистов в сфере экономики. Такими разделами являются: «Линейная алгебра», «Пределы функции»,«Дифференциальное исчисление», «Интегральное исчисление», «Дифференциальные уравнения» «Элементы теории вероятностей и математической статистики», «Понятие о линейном программировании».

В результате изучения данного курса учащиеся должны знать:

-основные математические понятия, необходимые для успешного усвоения изучаемого курса;

-методы решения математических задач, входящих в курс высшей математики.

Также учащиеся должны уметь:

-применять экономико-математические методы и модели для решения экономических задач;

-использовать математический аппарат для сознательного усвоения общепрофессиональных и специальных дисциплин.

Таким образом, преподавание предмета «Основы высшей математики» должно иметь не только общеобразовательную, но и профессиональную направленность. В результате изучения курса учащиеся должны усвоить, что математические понятия, являясь абстракцией свойств и отношений реального мира, обладают большой общностью и имеют широкую сферу применения. Эффективность преподавания курса во многом зависит от того, насколько удаётся преподавателю показать учащимся связь между изучаемой темой и их будущей специальностью. Качество усвоения того или иного вопроса программы заметно повышается, если в теоретический курс органически включены примеры, показывающие действенность математических методов в том роде деятельности, которую избрал себе учащийся.

ПРИМЕРНЫЙ ТЕМАТИЧЕСКИЙ ПЛАН

ПО ДИСЦИПЛИНЕ «ОСНОВЫ ВЫСШЕЙ МАТЕМАТИКИ»

Раздел, тема	Количество учебных часов	Время на самостоя- тельную работу учащихся (часов)
Всего	В том числе
Для дневной формы	Для заочной формы	На ус-тано-вочные занятия	На об-зорные занятия	На лабо-раторные, практи- ческие занятия
Раздел 1. Линейная алгебра 1.1.Определение матрицы. Действия над матрицами 1.2.Определитель матрицы. Свойства и вычисления 1.3.Обратная матрица Практическое занятие № 1 1.4 Системы линейных уравнений. Матрицы в экономических приложениях
Раздел 2. Пределы функций. Дифференциальное ис- числение 2.1. Предел функции в точке 2.2. Непрерывность функции Практическое занятие№ 2 2.3. Производная. Основные правила дифференци- рования 2.4. Применение производной к исследованию фун-кций 2.5 Применение понятий производной в экономике Практическое занятие№ 3 2.6. Функции нескольких переменных
Раздел 3. Интегральное исчисление 3.1. Неопределённый интеграл. Методы интегриро- вания 3.2. Определённый интеграл. Методы вычисления определённого интеграла 3.3. Приложения интеграла Практическое занятие№ 4
Раздел 4. Дифференциальные уравнения 4.1. Задачи, приводящие к понятию дифференциаль-ных уравнений. Основные определения 4.2. Дифференциальные уравнения 1-ого порядка Практическая работа № 5 4.3. Дифференциальные уравнения 2-ого порядка 4.2. Дифференциальные уравнения в экономике Практическое занятие№ 6
Раздел 5. Элементы теории вероятности 5.1. Случайные события. Вероятность события Основные теоремы теории вероятности 5.2. Случайная величина и её характеристики 5.3. Предмет математической статистики
Раздел 6. Понятие о линейном программировании 6.1. Решение систем линейных неравенств 6.2. Задачи линейного программирования. Этапы решения задач. 6.3. Транспортная задача		-
ИТОГО

СОДЕРЖАНИЕ

Пояснительная записка ........................................................................................................................

Примерный тематический план..........................................................................................................

Программное содержание курса..........................................................................................................

Краткое содержание курса...................................................................................................................

Методические указания к выполнению

домашней контрольной работе............................................................................................................

Теоретические вопросы к домашней

контрольной работе...............................................................................................................................

Задачи к домашней контрольной работе..……………………….……………………………….

Пример выполнения практической части

домашней контрольной работы……………………………………………..…………………………...……………………

Вопросы к ОКР по дисциплине

«Математика»………………..…………………………………………...………………………..

Список использованной литературы……………………………..………………….……………….……………………….

ПРОГРАММНОЕ СОДЕРЖАНИЕ КУРСА

Тема 1. Линейная алгебра.

1. Понятие о системе линейных уравнений с n-неизвестными.

2. Определители второго порядка.

3. Определители n-порядка, их свойства, вычисление.

4. Правило Крамера и метод Гаусса для систем n-линейных уравнений с n-неизвестными.

5. Матрица и её ранг. Вычисление ранга матрицы.

6. Операции над матрицами.

7. Матричный способ решения систем n-линейных уравнений с n-неизвестными.

Тема 2. Предел функции.

1. Свойства и графики элементарных функций.

2. Определение предела функции. Односторонние пределы. Два замечательных предела.

3. Основные теоремы о пределах.

4. Непрерывность элементарных функций.

5. Классификация точек разрыва функции.

Тема 3. Дифференциальное исчисление.

1. Определение производной. Геометрический и механический смысл производной.

2. Правила и таблица производных.

3. Определение дифференциала функции, его геометрический смысл.

4. Признаки возрастания. Убывания, постоянства функции.

5. Экстремум функции.

6. Выпуклость, вогнутость графика функции. Точки перегиба. Асимптоты графика функции.

7. Функция нескольких переменных. Частные производные. Полный дифференциал функции.

Тема 4. Интегральное исчисление.

1. Первообразная функция, неопределённый интеграл. Свойства неопределённого интеграла.

2. Способы интегрирования.

3. Определённый интеграл. Свойства определённого интеграла.

4. Площадь плоской фигуры.

5. Объёмы тел вращения

Тема 5. Дифференциальные уравнения.

1. Общее понятие дифференциального уравнения.

2. Уравнение 1-ого порядка. Геометрический смыл решений дифференциального уравнения 1-ого порядка.

3. Линейные однородные дифференциальные уравнения 2-ого порядка с постоянными коэффициентами.

4. Линейные неоднородные дифференциальные уравнения 2-ого порядка с постоянными коэффициентами.

КРАТКОЕ СОДЕРЖАНИЕ КУРСА

Тема 1. Линейная алгебра

Матрицей называют прямоугольную таблицу чисел, записанных в виде строк и столбцов.

А=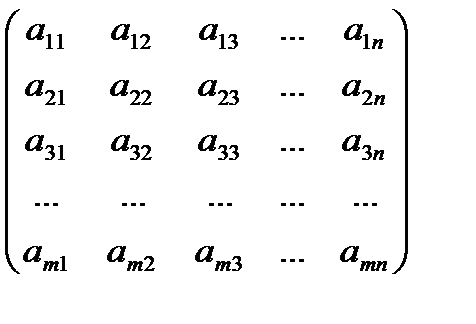

Каждой квадратной матрице можно поставить в соответствие число, вычисляемое определённым способом. Это число будем называть определителем. Обозначается Δ.

Для запоминания правила вычисления определителя третьего порядка используют модель Саррюса (Элементы определителя изображены точками.Перемножают элементы, соединенные линиями)

+ -

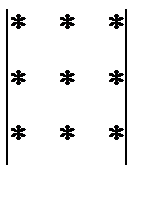
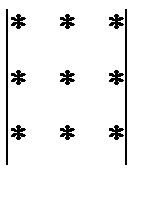
Минором элемента 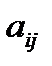определителя n-го порядка называется определитель (n-1)-го порядка, который состоит из элементов оставшихся после вычеркивания i-той строки, j-того столбца. Обозначается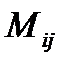

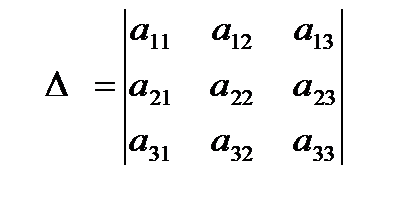
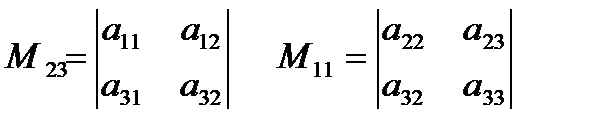
Алгебраическим дополнением элемента 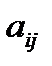называется произведение минора этого элемента на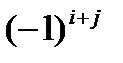

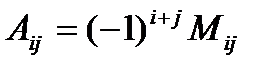
Матрица 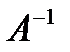называется обратной для матрицы А, если А 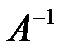= 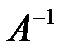А=Е (1)

Теорема

Если матрица А невырожденная, то существует обратная матрица 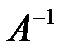, и притом только единственная, для которой выполняется равенство (1).

Вычисление обратной матрицы 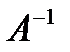для заданной матрицы А можно осуществить, руководствуясь следующим алгоритмом:

1.Проверяют, существует ли для матрицы А обратная матрица, т.е. является ли матрица А невырожденной. Для этого вычисляют определитель Δ (если Δ=0, то 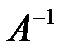не существует).

2.Для каждого элемента 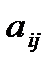исходной матрицы вычисляют алгебраические дополнения .

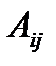3.Составляют присоединенную матрицу 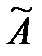, записав алгебраические дополнения элементов строк в столбцы.

4.Умножают элементы присоединенной матрицы на число 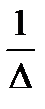, тем самым находят матрицу 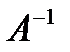, т.е. = .

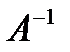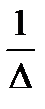
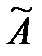5.Выполняют проверку справедливости равенства (1).

Системой m линейных уравнений с n неизвестными называется система вида:

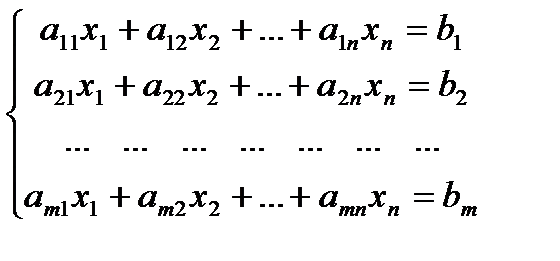(2)

где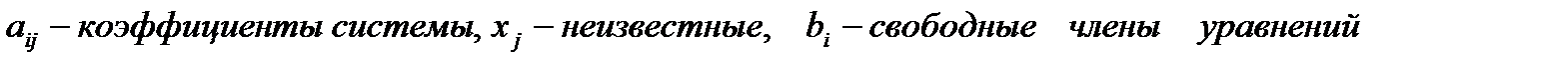

Для решения линейных систем используются следующие методы:

· использование обратной матрицы

Из коэффициентов системы составим матрицу А= 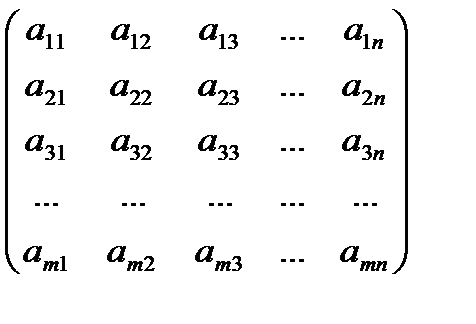,также введем в

рассмотрение матрицы-столбцы, состоящие соответственно из неизвестных и свободных членов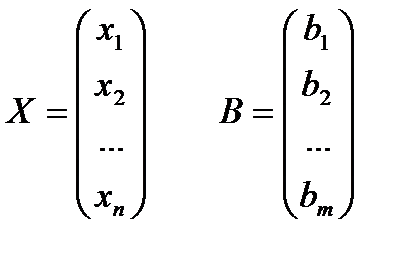

Тогда система (2) может быть записана в виде матричного уравнения АХ=В, для решения которого умножим его на 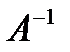слева. Получим, 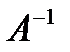АХ= В

ЕХ= В

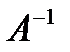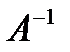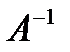Х= В

Итак, для нахождения решения необходимо найти матрицу 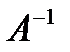, обратную для матрицы А, затем выполнить умножение матриц 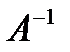и В.

· использование теоремы Крамера

Если определитель матрицы системы n линейных уравнений с n неизвестными отличен от нуля, то система имеет единственное решение, выражающееся формулами: 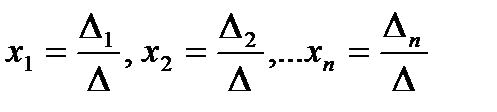, где Δ - определитель матрицы системы, 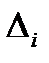- определители, полученные из Δ заменой в нём i-того столбца столбцом свободных членов.

· Метод Гаусса

Рассмотренные методы применимы только для решения систем n линейных уравнений с n неизвестными, имеющих невырожденную матрицу коэффициентов. Универсальным методом решения систем является метод Гаусса, который основан на приведении расширенной матрицы системы с помощью элементарных преобразований к трапецевидной форме.

Тема 2. Предел функции

Число А называется пределом функции у = f(x) в точке 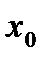, если для любой последовательности ( 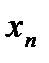), все члены которой принадлежат области определения функции, стремятся к 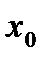, но не совпадают с ним соответствующая последовательность значений функции 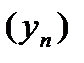стремится к точке А.

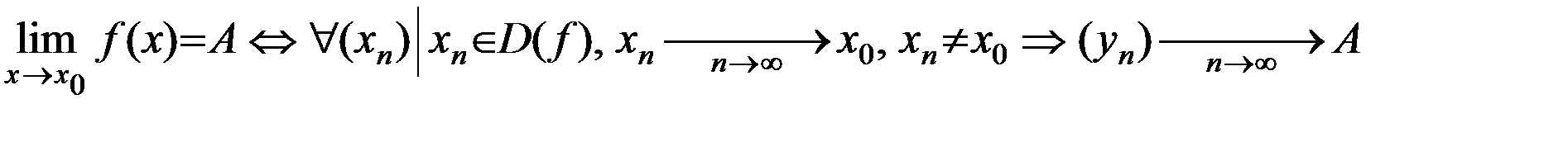
Теоремы о пределах функции в точке

1° Функция в точке может иметь только один предел.

2° Если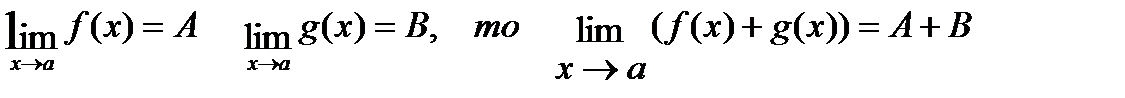

3°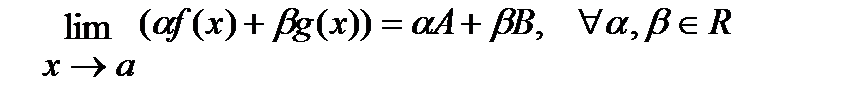

4°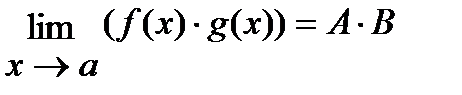

5° Если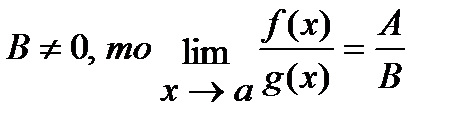

Если 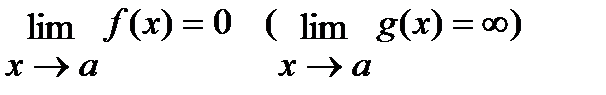в точке а, то функция f(x) называется бесконечно малой(БМФ) в точке а (функция g(x) называется бесконечно большой (ББФ) в точке а)

Теорема

Если f(x) – БМФ, то 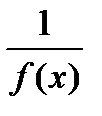- ББФ. Если g(x) – ББФ, то 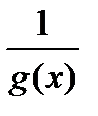- БМФ.

Первый замечательный предел

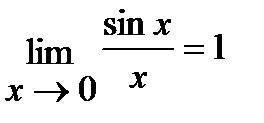
Второй замечательный предел

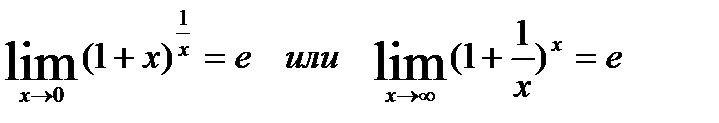
Определение

Функция у=f(x) называется непрерывной в точке 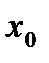, если:

1)функция определена в этой точке;

2)в некоторой окрестности точки 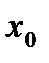существует предел функции в точке 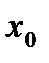, который совпадает со значением функции в этой точке.

Т.е.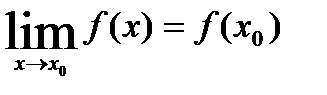

При невыполнении одного из этих условий функция терпит разрыв в точке .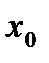

Рассмотрим классификацию точек разрыва.

Точка 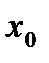называется точкой разрыва I рода функции f(x) , если в этой точке существуют конечные пределы справа и слева в точке 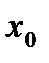, не равные друг другу.

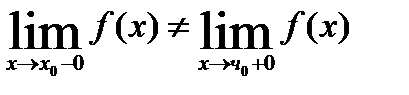
Точка 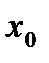называется точкой разрыва II рода функции f(x) , если в этой точке правый или левый пределы не существуют или являются бесконечными.

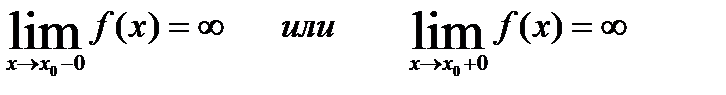
Асимптоты графика функции

ПрямаяL называется асимптотой кривой, заданной уравнением y = f(x), если расстояние между точками кривой и прямой стремится к нулю с удалением точки на кривой от начала координат.

Существуют вертикальные, наклонные или горизонтальные асимптоты.

х = а – вертикальная асимптота, если 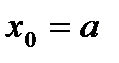- точка разрыва II рода

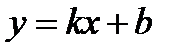- наклонная асимптота, если существуют конечныеk и b, которые вычисляются по формулам: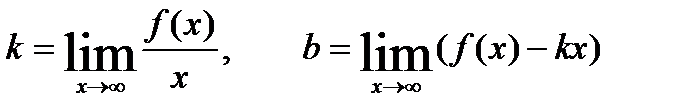

Если 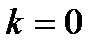, то 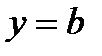- горизонтальная асимптота.

Тема 3. Дифференциальное исчисление

Правила дифференцирования

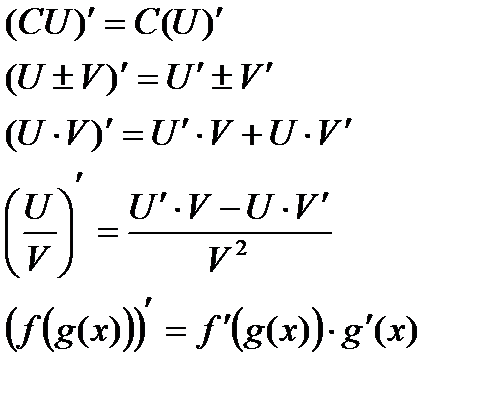
Таблица производных основных функций

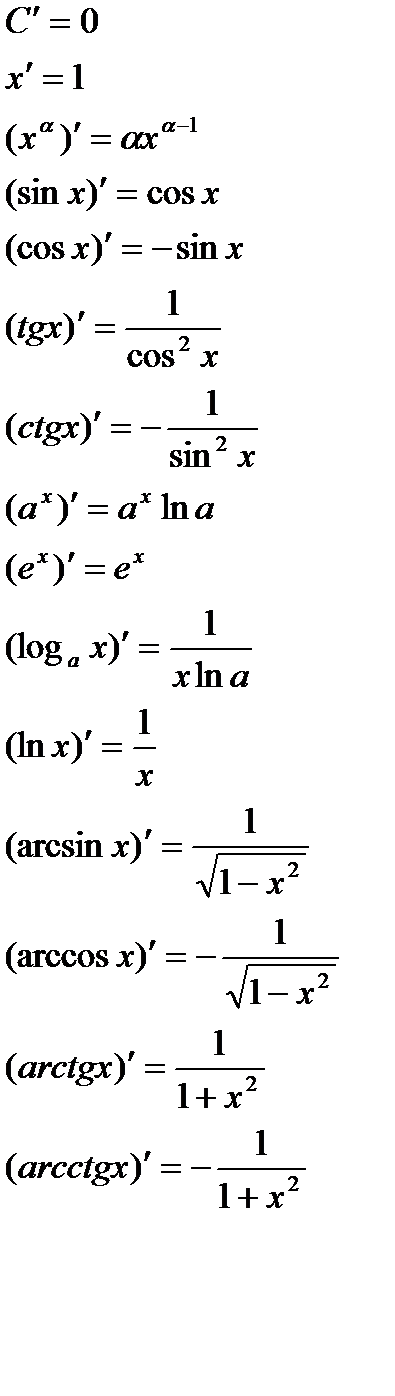
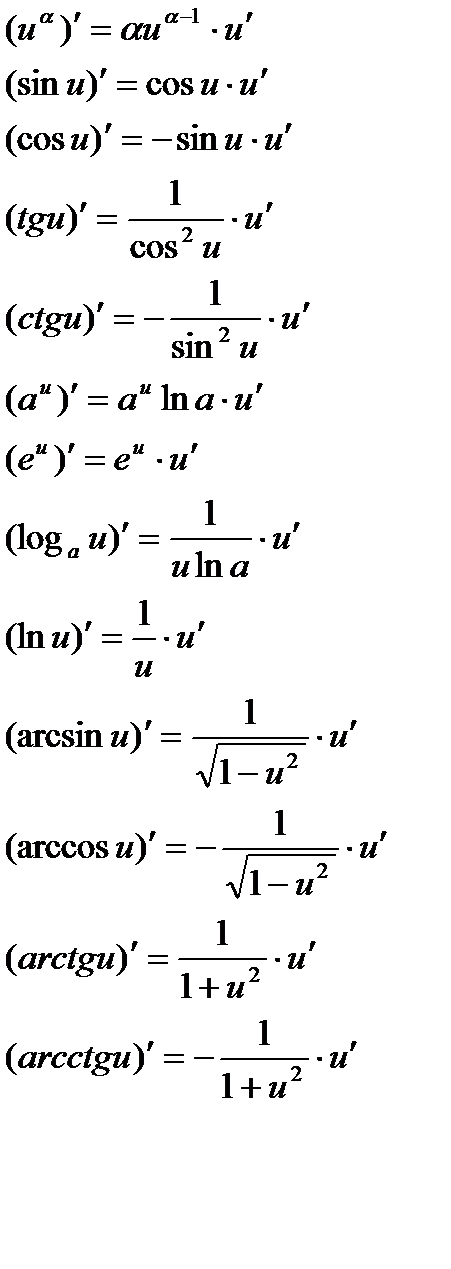
Геометрический смысл производной функции:

- производная 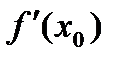функции 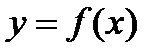равна угловому коэффициенту касательной, проведённой к графику данной функции в точке с абсциссой 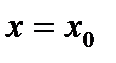, а также тангенсу угла наклона касательной к оси абсцисс.

Уравнение касательной, проведенной к кривой, заданной графиком 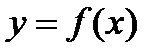, в точке М_о(х₀;у₀) с конечным угловым коэффициентом 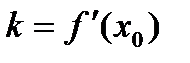запишется так:

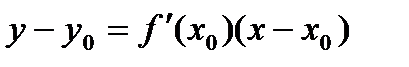
Из вышеизложенного видно, что наличие в точке графика функции 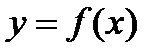касательной, непараллельной оси ординат (т.к. 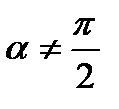), эквивалентно дифференцируемости функции в соответствующей точке.

Кроме касательной к графику функции в некоторой точке М_о(х₀;у₀)_, рассматривается и другая прямая, проходящая через эту точку.

Прямая, перпендикулярная касательной к кривой и проходящая через точку касания, называется нормалью к кривой. Из определения нормали следует, что её угловой коэффициент связан с угловым коэффициентом касательной равенством, выражающим условие перпендикулярности двух прямых.

Тогда уравнение нормали запишется так:

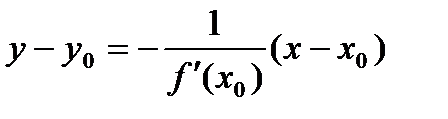
Функция y=f(x) называется возрастающей в промежутке 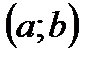, если для любых 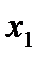и 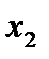, принадлежащих этому промежутку и таких , что 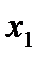< 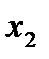, имеет место неравенство .

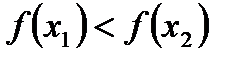х1 ,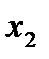

х2

f(х₂)

f(х₁)

х1

х2

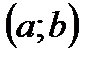Функция y=f(x) называется убывающей в промежутке , если для любых 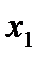и 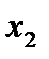, принадлежащих этому промежутку и таких , что 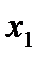< 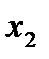, имеет место неравенство .

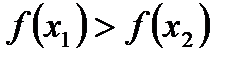f(x1)

f(x₂)

Как возрастающие, так и убывающие функции называются монотонными, а промежутки, в которых функция возрастает или убывает, - промежутками монотонности.

Возрастание и убывание функции y=f(x) характеризуется знаком её производной.

Теорема

Для того чтобы дифференцируемая на 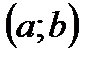функция y=f(x) не убывала (не возрастала) на этом интервале, необходимо и достаточно чтобы 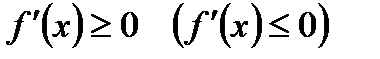для всех х из этого интервала.

Если же для любого х из 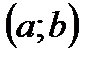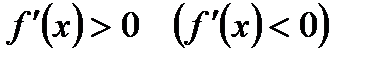то функция y=f(x) монотонно возрастает (монотонно убывает) на этом интервале.

Из теоремы следует, что для того чтобы функция y=f(x) была постоянной на 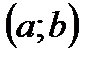, необходимо и достаточно, чтобы выполнялось условие: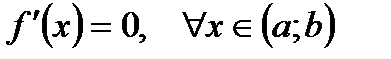

f´(x)<0

f´(x)=0

f´(x)<0

Внутренние точки области определения, в которых производная не существует или равна нулю, называются критическими.

Точка 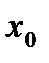из области определения D(f) точкой максимума (минимума) этой функции, если существует такой интервал 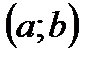, , 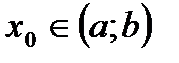не выходящий из области определения D(f), что для всех х ≠ 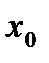, выполняется неравенство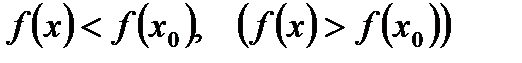

х0

f(х0)

х0

f(х0)

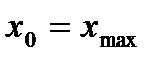
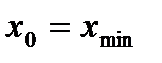
Точки максимума и минимума функции называются точками экстремума, а значения функции в этих точках – экстремумы функции.

Следующая теорема показывает, что точки экстремума следует искать среди критических точек функции.

Теорема Ферма

Если точка 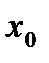- точка экстремума функции y=f(x) и в этой точке существует производная, то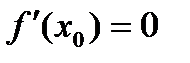

Свойство выпуклости (вогнутости) функции как и монотонности интуитивно понятно из геометрических представлений о графике функции:

а) б)

График а) естественно назвать выпуклым вверх, а график б) - выпуклым вниз.

Введем понятие выпуклости для дифференцируемых функций на интервале в каждой точке графика функции, в которой можно провести касательную.

Определение. Дифференцируемая на интервале (а;b) функция f(x) называется выпуклой вверх (вниз), если для любого 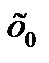и х из этого промежутка справедливо неравенство: ( )

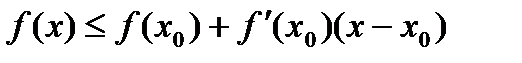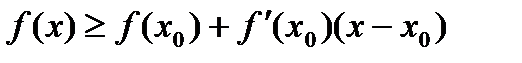Т.е. дифференцируемая функция выпуклая вверх (вниз) на (а;b) если все точки графика функции лежат не выше (не ниже) касательной, проведенной к графику функции в любой точке из (а;b).

Теорема(достаточное условие выпуклости функции)

Пусть функция у=f(x) определена и дважды дифференцируема на (а;b), существует 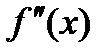тогда если 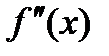>0 на(а;b), то на этом промежутке функция выпуклая вниз (вогнутая), если 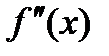<0, то на этом промежутке функция выпуклая вверх (выпуклая).

Определение. Точка 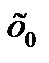из D(f) функции f(x) называется точкой перегиба, если:

1.в этой точке функция непрерывна;

2.существует интервал (а;b), 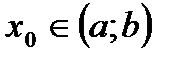такой, что на интервалах 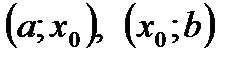направления выпуклости противоположны, т.е. в точке 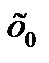выпуклость сменяется вогнутостью или наоборот.

х0

Теорема. (необходимое условие точки перегиба)

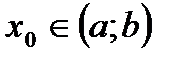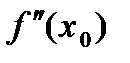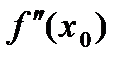Пусть дана функция у=f(x) дважды дифференцируемая на (а;b). Если в точке график имеет перегиб и существует конечная вторая производная , то =0.

Наиболее полное исследование функции и построение её графика можно провести по следующей схеме:

1. Найти область определения функции.

2. Четность, периодичность.

3. Исследовать функцию на непрерывность: наличие точек разрыва, их характеристика; асимптоты графика.

4. Найти точки пересечения графика с осями координат.

5. Определить критические точки, промежутки возрастания и убывания функции, а также экстремумы функции.

6. Найти интервалы выпуклости и вогнутости, точки перегиба.

7. Построение графика.

Тема 4. Интегральное исчисление.

Таблица основных неопределенных интегралов

1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 

1. 

14.

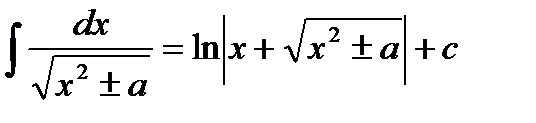
Методы интегрирования:

Правило подведения под знак дифференциала.

Правило основано на следующем очевидном утверждении, которое следует из инвариантности формы первого дифференциала: если 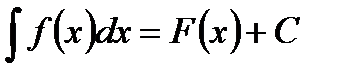, где х – независимая переменная, то верно и равенство 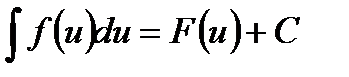, где u=u(x) – функция от х.

Например, 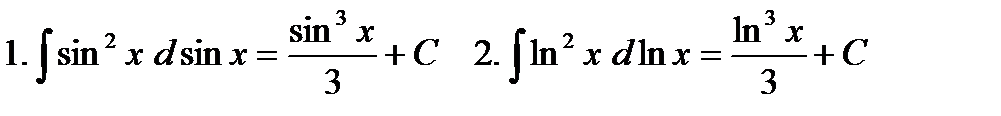ит.п.

На практике, исходный вид вычисленных интегралов обычно имеет другую форму:

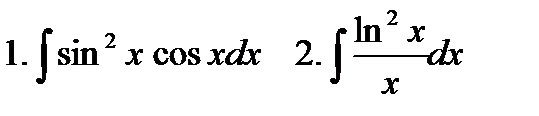и сведение их к табличным интегралам обеспечивается равенством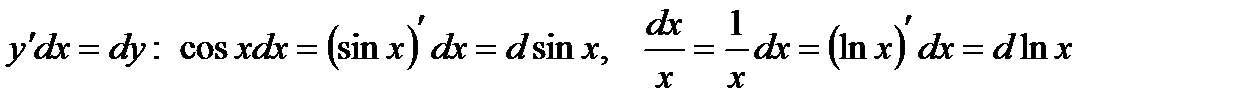

То есть, используется таблица производных, прочитанная справа-налево. В первом случае под знак дифференциала внесли cosx, во-втором - .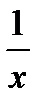

Правило замены переменной.

Утверждение, на котором основывается предыдущее правило, но записанное в ви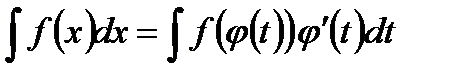де

, где 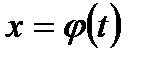- дифференцируемая функция, множество значений которой является областью определения функции 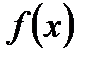. Естественно, как и ранее, мы предполагаем существование всех указанных интегралов. Из этой формулы следует и смысл замены переменной: функцию 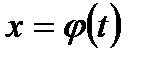стараются подобрать так, чтобы подынтегральное выражение 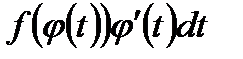, в полученном после преобразований интеграле, было проще исходного.

Правило интегрирования по частям.

Дифференциал произведения двух функци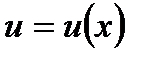й и 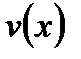определяется формулой 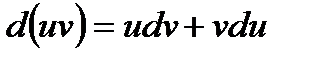. Перепишем равенство в виде 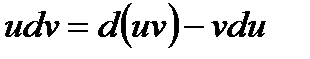и проинтегрируем обе части. С учетом свойств интеграла, получим формулу интегрирования по частям:

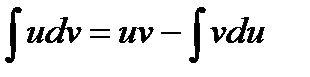
С помощью этой формулы обычно вычисляются интегралы от функций представляющих произведение многочлена на 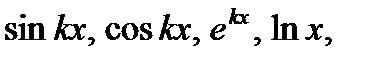причем в первых трех случаях за 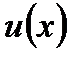обозначают многочлен, а в последнем 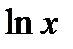. Поскольку в правой части формулы вместо функции 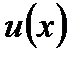появляется дифференциал этой функции 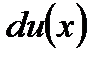, то есть возможность получить интеграл проще, если дифференциал функции проще, чем сама функция. После того как сама функция 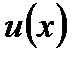выбрана, оставшееся под интегралом выражение обозначаем 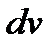, тогда сама функция .

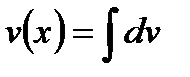Определённый интеграл. Определённым называется интеграл с заданными пределами

интегрирования:

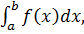где а-нижний предел интегрирования, b-верхний предел предел интегрирования.

Формула Ньютона-Лейбница

Пусть 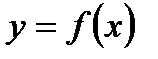непрерывна на 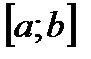и переменная 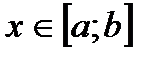. Тогда совокупность всех первообразных для этой функции можно выразить формулой 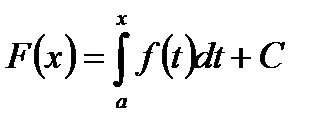. Легко видеть, что 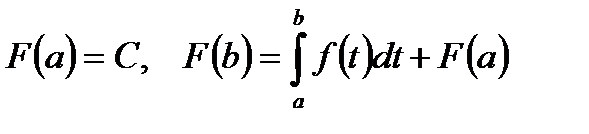. Откуда, заменив переменную интегрирования снова на х, получим формулу Ньютона –Лейбница:

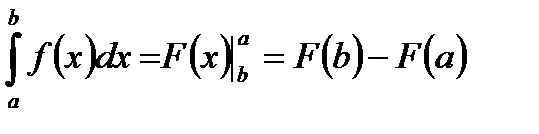
Для того чтобы вычислить определенный интеграл, прежде всего вычисляется одна из первообразных F(x), затем вычисляется значение этой функции в точке b и вычитается её значение в точке а.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ

ДОМАШНЕЙ КОНТРОЛЬНОЙ РАБОТЫ.

Заочная форма обучения почти полностью основана на самостоятельной работе учащихся с учебной литературой. Каждому учащемуся предлагается выполнить контрольную работу по курсу «Основы высшей математики».

Начинать работу необходимо с тщательного изучения данных методических рекомендаций. Далее надо подобрать необходимую литературу.

Отдельные источники рекомендованы в настоящих методических рекомендациях. Однако, в процессе написания работ можно привлечь дополнительную литературу, более углубленно рассматривающую различные аспекты темы. В случае затруднения в выборе литературы можно обратиться за консультацией к преподавателю.

Самостоятельное изучение курса следует начинать с ознакомления с программой курса. Затем следует перейти к последовательному изучению курса. При этом изучение теоретического материала и разбор типовых задач должны чередоваться с попытками самостоятельного решения задач по изучаемой теме. Признаком того, что материал полностью освоен, является умение учащегося самостоятельно воспроизводить формулировки основных определений, теорем, восстанавливать доказательства, решать задачи.

Учащийся должен выполнить контрольную работу, строго придерживаясь указанных ниже правил:

1. Вариант контрольной работы определяется по шифру учащегося

2. Контрольная работа должна быть выполнена в установленные учебным графиком сроки, написана грамотно, разборчиво, с полями для замечаний рецензента.

3. Ответ на теоретический вопрос должен составить по объёму 3-4 страницы ученической тетради, быть конкретным и полным, при необходимости – дополнен подтверждающими примерами.

4. Решения практических задач необходимо излагать подробно и аккуратно, поясняя все действия, производя ссылки на применяемые формулы и делая необходимые чертежи.

5. Недопустимым является сокращение слов, небрежное оформление работы.

6. В конце выполнения контрольной работы следует указать использованную литературу, поставить дату выполнения работы, личную подпись.

7. Объем контрольной работы должен составлять примерно 20-22 страницы тетрадного формата или 8-12 листов машинописного или компьютерного набора, страницы должны быть пронумерованы. Необходимо оставить 1 листок для рецензии преподавателя.

8. После получения прорецензированной работы необходимо внимательно ознакомиться с рецензией, с учётом замечаний и рекомендаций доработать отдельные вопросы и предъявить преподавателю при сдаче экзамена.

ТЕОРЕТИЧЕСКИЕ ВОПРОСЫ