Общая форма записи модели задачи ЛП
Целевая функция (ЦФ)  , при ограничениях , при ограничениях 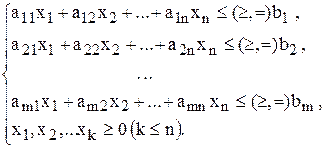 | (1.1) |
При описании реальной ситуации с помощью линейной модели следует проверять наличие у модели таких свойств, как пропорциональность и аддитивность. Пропорциональность означает, что вклад каждой переменной в ЦФ и общий объем потребления соответствующих ресурсов должен быть прямо пропорционален величине этой переменной. Например, если продавая j-й товар в общем случае по цене 100 рублей, фирма будет делать скидку при определенном уровне закупки до уровня цены 95 рублей, то будет отсутствовать прямая пропорциональность между доходом фирмы и величиной переменной  . Т.е. в разных ситуациях одна единица j-го товара будет приносить разный доход. Аддитивность означает, что ЦФ и ограничения должны представлять собой сумму вкладов от различных переменных. Примером нарушения аддитивности служит ситуация, когда увеличение сбыта одного из конкурирующих видов продукции, производимых одной фирмой, влияет на объем реализации другого.
. Т.е. в разных ситуациях одна единица j-го товара будет приносить разный доход. Аддитивность означает, что ЦФ и ограничения должны представлять собой сумму вкладов от различных переменных. Примером нарушения аддитивности служит ситуация, когда увеличение сбыта одного из конкурирующих видов продукции, производимых одной фирмой, влияет на объем реализации другого.
Допустимое решение– это совокупность чисел (план)  , удовлетворяющих ограничениям задачи (1.1).
, удовлетворяющих ограничениям задачи (1.1).
Оптимальное решение – это план, при котором ЦФ принимает свое максимальное (минимальное) значение.
Методические рекомендации
Задача № 1.01
Фабрика производит два вида красок: первый – для наружных, а второй – для внутренних работ. Для производства красок используются два ингредиента: А и В. Максимально возможные суточные запасы этих ингредиентов составляют 6 и 8 т соответственно. Известны расходы А и В на 1 т соответствующих красок (табл. 1.1). Изучение рынка сбыта показало, что суточный спрос на краску 2-го вида никогда не превышает спроса на краску 1-го вида более, чем на 1 т. Кроме того, установлено, что спрос на краску 2-го вида никогда не превышает 2 т в сутки. Оптовые цены одной тонны красок равны: 3 тыс. руб. для краски 1-го вида; 2 тыс. руб. для краски 2-го вида.
Необходимо построить математическую модель, позволяющую установить, какое количество краски каждого вида надо производить, чтобы доход от реализации продукции был максимальным.
Таблица 1.1
Параметры задачи о производстве красок
| Ингредиенты | Расход ингредиентов, т ингр./т краски | Запас, т ингр./сутки | |
| Краска 1-го вида | Краска 2-го вида | ||
| А | |||
| В |
Решение
Прежде чем построить математическую модель задачи, т.е. записать ее с помощью математических символов, необходимо четко разобраться с экономической ситуацией, описанной в условии. Для этого необходимо с точки зрения экономики, а не математики, ответить на следующие вопросы:
1) Что является искомыми величинами задачи?
2) Какова цель решения? Какой параметр задачи служит критерием эффективности (оптимальности) решения, например, прибыль, себестоимость, время и т.д. В каком направлении должно изменяться значение этого параметра (к max или к min) для достижения наилучших результатов?
3) Какие условия в отношении искомых величин и ресурсов задачи должны быть выполнены? Эти условия устанавливают, как должны соотноситься друг с другом различные параметры задачи, например, количество ресурса, затраченного при производстве, и его запас на складе; количество выпускаемой продукции и емкость склада, где она будет храниться; количество выпускаемой продукции и рыночный спрос на эту продукцию и т.д.
Только после экономического ответа на все эти вопросы можно приступать к записи этих ответов в математическом виде, т.е. к записи математической модели.
1) Искомые величины являются переменными задачи, которые как правило обозначаются малыми латинскими буквами с индексами, например, однотипные переменные удобно представлять в виде  .
.
2) Цель решения записывается в виде целевой функции, обозначаемой, например, 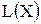 . Математическая формула ЦФ
. Математическая формула ЦФ 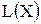 отражает способ расчета значений параметра – критерия эффективности задачи.
отражает способ расчета значений параметра – критерия эффективности задачи.
3) Условия, налагаемые на переменные и ресурсы задачи, записываются в виде системы равенств или неравенств, т.е. ограничений. Левые и правые части ограничений отражают способ получения (расчет или численные значения из условия задачи) значений тех параметров задачи, на которые были наложены соответствующие условия.
В процессе записи математической модели необходимо указывать единицы измерения переменных задачи, целевой функции и всех ограничений.
Построим модель задачи №1.01, используя описанную методику.
Переменные задачи
В задаче №1.01 требуется установить, сколько краски каждого вида надо производить. Поэтому искомыми величинами, а значит, и переменными задачи являются суточные объемы производства каждого вида красок:
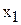 – суточный объем производства краски 1-го вида, [т краски/сутки];
– суточный объем производства краски 1-го вида, [т краски/сутки];
 – суточный объем производства краски 2-го вида, [т краски/сутки].
– суточный объем производства краски 2-го вида, [т краски/сутки].
Целевая функция
В условии задачи №1.01 сформулирована цель – добиться максимального дохода от реализации продукции. Т.е. критерием эффективности служит параметр суточного дохода, который должен стремится к максимуму.Чтобы рассчитать величину суточного дохода от продажи краскок обоих видов, необходимо знать объемы производства красок, т.е. 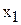 и
и  т краски в сутки, а также оптовые цены на краски 1-го и 2-го видов – согласно условию, соответственно 3 и 2 тыс.руб. за 1 т краски. Таким образом, доход от продажи суточного объема производства краски 1-го вида равен
т краски в сутки, а также оптовые цены на краски 1-го и 2-го видов – согласно условию, соответственно 3 и 2 тыс.руб. за 1 т краски. Таким образом, доход от продажи суточного объема производства краски 1-го вида равен  тыс.руб. в сутки, а от продажи краски 2-го вида –
тыс.руб. в сутки, а от продажи краски 2-го вида –  тыс.руб. в сутки. Поэтому запишем ЦФ в виде суммы дохода от продажи красок 1-го и 2-го видов (при допущении независимости объемов сбыта каждой из красок)
тыс.руб. в сутки. Поэтому запишем ЦФ в виде суммы дохода от продажи красок 1-го и 2-го видов (при допущении независимости объемов сбыта каждой из красок)
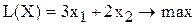 [тыс.руб./сутки],
[тыс.руб./сутки],
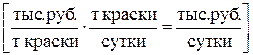 .
.
Ограничения
Возможные объемы производства красок 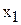 и
и  ограничиваются следующими условиями:
ограничиваются следующими условиями:
· количество ингредиентов А и В, израсходованное в течение суток на производство красок обоих видов, не может превышать суточного запаса этих ингредиентов на складе;
· согласно результатам изучения рыночного спроса суточный объем производства краски 2-го вида может превышать объем производства краски 1-го вида, но не более, чем на 1 т краски;
· объем производства краски 2-го вида не должен превышать 2 т в сутки, что также следует из результатов изучения рынков сбыта;
· объемы производства красок не могут быть отрицательными.
Таким образом, все ограничения задачи №1.01 делятся на 3 группы, обусловленные:
1) расходом ингредиентов;
2) рыночным спросом на краску;
3) неотрицательностью объемов производства.
Ограничения по расходу любого из ингредиентов имеют следующую содержательную форму записи
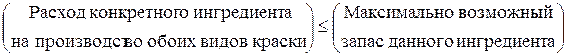 .
.
Запишем эти ограничения в математической форме.
Левая часть ограничения – это формула расчета суточного расхода конкретного ингредиента на производство красок. Так из условия известен расход ингредиента А на производство 1 т краски 1-го вида (1 т ингр. А) и 1 т краски 2-го вида (2 т ингр. А) (см. табл.1.1). Тогда на производство 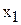 т краски 1-го вида и
т краски 1-го вида и 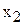 т краски 2-го вида потребуется
т краски 2-го вида потребуется  т ингр. А.
т ингр. А.
Правая часть ограничения – это величина суточного запаса ингредиента на складе, например, 6 т ингредиента А в сутки (см. табл.1.1). Таким образом, ограничение по расходу А имеет вид
 .
.
Аналогична математическая запись ограничения по расходу В
 .
.
Примечание 1.1. Следует всегда проверять размерность левой и правой части каждого из ограничений, поскольку их несовпадение свидетельствует о принципиальной ошибке при составлении ограничений.
Ограничение по суточному объему производства краски 1-го вида по сравнению с объемом производства краски 2-го вида имеет
содержательную форму
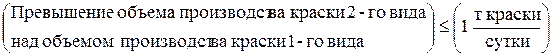
и математическую форму
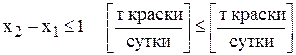 .
.
Ограничение по суточному объему производства краски 1-го вида имеет
содержательную форму

и математическую форму
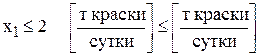 .
.
Неотрицательность объемов производства задается как
 .
.
Таким образом, математическая модель этой задачи имеет вид
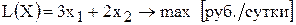

Задача №1.02
Выполнить заказ по производству 32 изделий 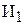 и 4 изделий
и 4 изделий 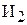 взялись бригады
взялись бригады 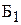 и
и 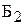 . Производительность бригады
. Производительность бригады 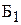 по производству изделий
по производству изделий 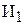 и
и 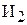 составляет соответственно 4 и 2 изделия в час, фонд рабочего времени этой бригады 9,5 ч. Производительность бригады
составляет соответственно 4 и 2 изделия в час, фонд рабочего времени этой бригады 9,5 ч. Производительность бригады 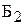 – соответственно 1 и 3 изделия в час, а ее фонд рабочего времени – 4 ч. Затраты, связанные с производством единицы изделия, для бригады
– соответственно 1 и 3 изделия в час, а ее фонд рабочего времени – 4 ч. Затраты, связанные с производством единицы изделия, для бригады 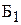 равны соответственно 9 и 20 руб., для бригады
равны соответственно 9 и 20 руб., для бригады 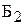 – 15 и 30 руб.
– 15 и 30 руб.
Составьте математическую модель задачи, позволяющую найти оптимальный объем выпуска изделий, обеспечивающий минимальные затраты на выполнение заказа.
Решение
Переменные задачи
Искомыми величинами в задаче являются объемы выпуска изделий. Изделия 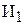 будут выпускаться двумя бригадами
будут выпускаться двумя бригадами 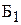 и
и 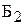 . Поэтому необходимо различать количество изделий
. Поэтому необходимо различать количество изделий 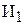 , произведенных бригадой
, произведенных бригадой 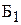 , и количество изделий И1, произведенных бригадой
, и количество изделий И1, произведенных бригадой 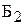 . Аналогично, объемы выпуска изделий
. Аналогично, объемы выпуска изделий 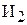 бригадой
бригадой 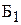 и бригадой
и бригадой 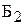 также являются различными величинами. Вследствие этого в данной задаче 4 переменные. Для удобства восприятия будем использовать двухиндексную форму записи
также являются различными величинами. Вследствие этого в данной задаче 4 переменные. Для удобства восприятия будем использовать двухиндексную форму записи 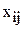 – количество изделий
– количество изделий 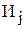 (j=1,2), изготавливаемых бригадой
(j=1,2), изготавливаемых бригадой  (i=1,2), а именно,
(i=1,2), а именно,
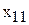 – количество изделий – количество изделий 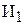 , изготавливаемых бригадой , изготавливаемых бригадой 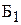 , [шт.]; , [шт.]; 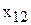 – количество изделий – количество изделий 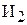 , изготавливаемых бригадой , изготавливаемых бригадой 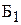 , [шт.]; , [шт.];  – количество изделий – количество изделий 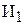 , изготавливаемых бригадой , изготавливаемых бригадой 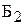 , [шт.]; , [шт.];  – количество изделий – количество изделий 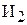 , изготавливаемых бригадой , изготавливаемых бригадой 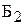 , [шт.]. , [шт.]. |
Примечание 1.2.В данной задаче нет необходимости привязываться к какому-либо временному интервалу (в задаче №1.01 была привязка к суткам), поскольку здесь требуется найти не объем выпуска за определенное время, а способ распределения известной плановой величины заказа между бригадами.
Целевая функция
Целью решения задачи является выполнение плана с минимальными затратами, т.е. критерием эффективности решения служит показатель затрат на выполнение всего заказа. Поэтому ЦФ должна быть представлена формулой расчета этих затрат. Затраты каждой бригады на производство одного изделия 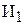 и
и 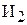 известны из условия. Таким образом, ЦФ имеет вид
известны из условия. Таким образом, ЦФ имеет вид
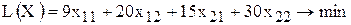 ,
,
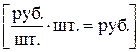 .
.
Ограничения
Возможные объемы производства изделий бригадами ограничиваются следующими условиями:
· общее количество изделий 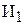 , выпущенное обеими бригадами, должно равняться 32 шт., а общее количество изделий
, выпущенное обеими бригадами, должно равняться 32 шт., а общее количество изделий 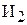 – 4 шт.;
– 4 шт.;
· время, отпущенное на работу над данным заказом, составляет для бригады 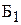 – 9,5 ч, а для бригады
– 9,5 ч, а для бригады 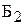 – 4 ч;
– 4 ч;
· объемы производства изделий не могут быть отрицательными величинами.
Таким образом, все ограничения задачи №1.02 делятся на 3 группы, обусловленные:
1) величиной заказа на производство изделий;
2) фондами времени, выделенными бригадам;
3) неотрицательностью объемов производства.
Для удобства составления ограничений запишем исходные данные в виде таблицы 1.2.
Таблица 1.2
