Порядок выполнения работы. 1. Включите компьютер
1. Включите компьютер. Загрузите пакет «Открытая физика 2.5» часть 1.
2. Кликните левой кнопкой компьютерной мыши в содержании раздел «Механика» на любую строку.
3. В верхнем правом углу расположено меню, которое содержит теорию, вопросы, задачи, задачи с решениями, лабораторные работы, журнал. Кликните мышью раздел «Лабораторные работы» (весы).
4. Перед Вами лабораторная работа №1.6 «Движение брусков».

5. На рисунке изображены три тела, соединенные между собой нитью, перекинутой через блок. Два тела находятся на поверхности стола, третье – висит на нити. Нажмите «Старт». Тела начнут двигаться. Слева под рисунком находятся параметры – массы тел, которые можно изменять. Справа под рисунком приведены значения ускорения 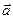 , силы натяжения нити Т, сил взаимодействия между двумя телами, лежащими на столе
, силы натяжения нити Т, сил взаимодействия между двумя телами, лежащими на столе  .
.
6. Установите параметры по указанию преподавателя. Нажмите «Старт».
7. Пронаблюдайте движение брусков.
8. Повторите моделирование несколько раз (по указанию преподавателя).
9. Зарисуйте рисунок в тетрадь, запишите полученные результаты, либо распечатайте результат на принтере.
10. Ответьте на вопросы и решите задачи, расположенные в правой половине экрана.
11. Дома проработайте модели 1.10, 1.11 из раздела «Модели».
12. Кликните мышью «Журнал». Обнулите результаты в таблице, нажав кнопку «Сброс результатов».
13. Проведите минитестирование. Ответьте на вопросы из раздела «Вопросы» и решите задачи из раздела «Задачи». Результат сообщите преподавателю.
14. Напишите вывод.
3. Контрольные вопросы
1. Что изучает динамика?
2. Что такое изолированная система?
3. Что изучает классическая, релятивистская, квантовая механика?
4. Какая система называется инерциальной? Сформулируйте первый закон Ньютона.
5. Что такое инерция?
6. В чем заключается физический смысл массы? Закон сохранения массы.
7. Сформулируйте физический смысл силы. Какая сила называется равнодействующей?
8. Сформулируйте второй закон Ньютона.
9. Сформулируйте третий закон Ньютона.
10. Какие силы называются внутренними?
Лабораторная работа № 4
Законы сохранения в механике.
Упругие и неупругие соударения
Цель работы: изучение законов сохранения в механике, упругих и неупругих соударений, моделей.
Краткая теория
Пусть на тело массой m в течение некоторого малого промежутка времени Δt действовала сила 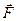 Под действием этой силы скорость тела изменилась на
Под действием этой силы скорость тела изменилась на  . Следовательно, в течение времени Δt тело двигалось с ускорением
. Следовательно, в течение времени Δt тело двигалось с ускорением
 | (1.1) |
Из основного закона динамики (второго закона Ньютона) следует:
 | (1.2) |
Физическая величина, равная произведению массы тела на скорость его движения, называется импульсом тела (или количеством движения). Импульс тела – векторная величина. Единицей измерения импульса в СИ является килограмм-метр в секунду (кг·м/с).
Физическая величина, равная произведению силы на время ее действия, называется импульсом силы. Импульс силы также является векторной величиной.
Второй закон Ньютона (или закон изменения импульса) может быть сформулирован следующим образом: изменение импульса тела (количества движения) равно импульсу силы.
Обозначив импульс тела буквой  второй закон Ньютона можно записать в виде
второй закон Ньютона можно записать в виде
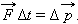 | (1.3) |
Именно в таком общем виде сформулировал второй закон сам Ньютон. Сила 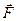 в этом выражении представляет собой равнодействующую всех сил, приложенных к телу. Это векторное равенство может быть записано в проекциях на координатные оси:
в этом выражении представляет собой равнодействующую всех сил, приложенных к телу. Это векторное равенство может быть записано в проекциях на координатные оси:
| FxΔt = Δpx; FyΔt = Δpy; FzΔt = Δpz. | (1.4) |
Изучите модель «Импульс тела».
 | Модель предназначена для иллюстрации понятий импульса тела mυ и импульса силы FΔt. Демонстрируется изменение импульса тела при воздействии на него силы. Можно выбирать начальную скорость υ0 бруска, его массу m, модуль и направление действующей силы F и время Δt ее действия. После прекращения действия силы брусок движется с другой скоростью. Количественно проверяется закон изменения импульса |
| Модель. Импульс тела. |
Таким образом, изменение проекции импульса тела на любую из трех взаимно перпендикулярных осей равно проекции импульса силы на эту же ось. Рассмотрим в качестве примера одномерное движение, т. е. движение тела по одной из координатных осей (например, оси OY). Пусть тело свободно падает с начальной скоростью υ0 под действием силы тяжести; время падения равно t. Направим ось OY вертикально вниз. Импульс силы тяжести Fт = mg за время t равен mgt. Этот импульс равен изменению импульса тела
| Fтt = mgt = Δp = m(υ – υ0), откуда υ = υ0 + gt. |
Этот простой результат совпадает с кинематической формулой для скорости равноускоренного движения. В этом примере сила оставалась неизменной по модулю на всем интервале времени t. Если сила изменяется по величине, то в выражение для импульса силы нужно подставлять среднее значение силы Fср на промежутке времени ее действия. Рис. 1.1 иллюстрирует метод определения импульса силы, зависящей от времени.
 Рис. 1.1. Вычисление импульса силы по графику зависимости F(t). Рис. 1.1. Вычисление импульса силы по графику зависимости F(t). | Выберем на оси времени малый интервал Δt, в течение которого сила F(t) практически остается неизменной. Импульс силы F(t)Δt за время Δt будет равен площади заштрихованного столбика. Если всю ось времени на интервале от 0 до t разбить на малые интервалы Δti, а затем просуммировать импульсы силы на всех интервалах Δti, то суммарный импульс силы окажется равным площади, |
которую образует ступенчатая кривая с осью времени. В пределе (Δti → 0) эта площадь равна площади, ограниченной графиком F(t) и осью t. Этот метод определения импульса силы по графику F(t) является общим и применим для любых законов изменения силы со временем. Математически задача сводится к интегрированию функции F(t) на интервале [0; t].
Импульс силы, график которой представлен на рис. 1.1, на интервале от t1 = 0 с до t2 = 10 с равен:
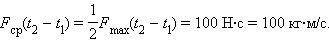 |
В этом простом примере  В некоторых случаях среднюю силу Fср можно определить, если известно время ее действия и сообщенный телу импульс. Например, сильный удар футболиста по мячу массой 0,415 кг может сообщить ему скорость υ=30 м/с. Время удара приблизительно равно 8·10–3 с.
В некоторых случаях среднюю силу Fср можно определить, если известно время ее действия и сообщенный телу импульс. Например, сильный удар футболиста по мячу массой 0,415 кг может сообщить ему скорость υ=30 м/с. Время удара приблизительно равно 8·10–3 с.
Импульс p, приобретенный мячом в результате удара есть:
| p = mυ = 12,5 кг·м/с. |
Следовательно, средняя сила Fср, с которой нога футболиста действовала на мяч во время удара, есть:
 |
Это очень большая сила. Она приблизительно равна весу тела массой 160 кг.
Если движение тела во время действия силы происходило по некоторой криволинейной траектории, то начальный  и конечный
и конечный  импульсы тела могут отличаться не только по модулю, но и по направлению. В этом случае для определения изменения импульса
импульсы тела могут отличаться не только по модулю, но и по направлению. В этом случае для определения изменения импульса  удобно использовать диаграмму импульсов, на которой изображаются вектора
удобно использовать диаграмму импульсов, на которой изображаются вектора  и
и  , а также вектор
, а также вектор  построенный по правилу параллелограмма. В качестве примера на рис. 1.2 изображена диаграмма импульсов для мяча, отскакивающего от шероховатой стенки. Мяч массой m налетел на стенку со скоростью
построенный по правилу параллелограмма. В качестве примера на рис. 1.2 изображена диаграмма импульсов для мяча, отскакивающего от шероховатой стенки. Мяч массой m налетел на стенку со скоростью  под углом α к нормали (ось OX) и отскочил от нее со скоростью
под углом α к нормали (ось OX) и отскочил от нее со скоростью 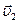 под углом β. Во время контакта со стеной на мяч действовала некоторая сила
под углом β. Во время контакта со стеной на мяч действовала некоторая сила 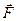 направление которой совпадает с направлением вектора
направление которой совпадает с направлением вектора 
 Рис. 1.2. Отскок мяча от шероховатой стенки и диаграмма импульсов. Рис. 1.2. Отскок мяча от шероховатой стенки и диаграмма импульсов. | При нормальном падении мяча массой m на упругую стенку со скоростью  после отскока мяч будет иметь скорость после отскока мяч будет иметь скорость  . Следовательно, изменение импульса мяча за время отскока равно . Следовательно, изменение импульса мяча за время отскока равно  . В проекциях на ось OX этот результат можно записать в скалярной форме Δpx = –2mυx. . В проекциях на ось OX этот результат можно записать в скалярной форме Δpx = –2mυx. |
Ось OX направлена от стенки (как на рис. 1.2), поэтому υx < 0 и Δpx > 0. Следовательно, модуль Δp изменения импульса связан с модулем υ скорости мяча соотношением Δp = 2mυ.
При взаимодействии тел импульс одного тела может частично или полностью передаваться другому телу. Если на систему тел не действуют внешние силы со стороны других тел, такая система называется замкнутой.
В замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой.
Этот фундаментальный закон природы называется законом сохранения импульса. Он является следствием из второго и третьего законов Ньютона.
Рассмотрим какие-либо два взаимодействующих тела, входящих в состав замкнутой системы. Силы взаимодействия между этими телами обозначим через  и
и  . По третьему закону Ньютона
. По третьему закону Ньютона  . Если эти тела взаимодействуют в течение времени t, то импульсы сил взаимодействия одинаковы по модулю и направлены в противоположные стороны:
. Если эти тела взаимодействуют в течение времени t, то импульсы сил взаимодействия одинаковы по модулю и направлены в противоположные стороны:  . Применим к этим телам второй закон Ньютона:
. Применим к этим телам второй закон Ньютона:
 |
где  и
и  – импульсы тел в начальный момент времени,
– импульсы тел в начальный момент времени,  и
и  – импульсы тел в конце взаимодействия. Из этих соотношений следует:
– импульсы тел в конце взаимодействия. Из этих соотношений следует:
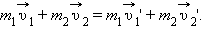 | (1.5) |
Это равенство означает, что в результате взаимодействия двух тел их суммарный импульс не изменился. Рассматривая теперь всевозможные парные взаимодействия тел, входящих в замкнутую систему, можно сделать вывод, что внутренние силы замкнутой системы не могут изменить ее суммарный импульс, т. е. векторную сумму импульсов всех тел, входящих в эту систему.
 Рис. 1.3. Нецентральное соударение шаров разных масс: 1 – импульсы до соударения; 2 – импульсы после соударения; 3 – диаграмма импульсов. Рис. 1.3. Нецентральное соударение шаров разных масс: 1 – импульсы до соударения; 2 – импульсы после соударения; 3 – диаграмма импульсов. | Рис. 1.3 иллюстрирует закон сохранения импульса на примере нецентрального соударения двух шаров разных масс, один из которых до соударения находился в состоянии покоя. Изображенные на рис. 1.3 вектора импульсов шаров до и после соударения можно спроектировать на координатные оси OX и OY. Закон сохранения импульса выполняется и для проекций векторов на каждую ось. В частности, из диаграммы импульсов (рис. 1.3) следует, что проекции векторов 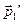 и и  импульсов обоих шаров после соударения на ось OY должны быть одинаковы по модулю и иметь разные знаки, чтобы их сумма равнялась нулю. импульсов обоих шаров после соударения на ось OY должны быть одинаковы по модулю и иметь разные знаки, чтобы их сумма равнялась нулю. |
Закон сохранения импульса во многих случаях позволяет находить скорости взаимодействующих тел даже тогда, когда значения действующих сил неизвестны. Примером может служить реактивное движение.
При стрельбе из орудия возникает отдача – снаряд движется вперед, а орудие – откатывается назад. Снаряд и орудие – два взаимодействующих тела. Скорость, которую приобретает орудие при отдаче, зависит только от скорости снаряда и отношения масс (рис. 1.4). Если скорости орудия и снаряда обозначить через 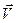 и
и 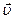 , а их массы через М и m, то на основании закона сохранения импульса можно записать в проекциях на ось OX
, а их массы через М и m, то на основании закона сохранения импульса можно записать в проекциях на ось OX
 | |||||
 Рис. 1.4. Отдача при выстреле из орудия. Рис. 1.4. Отдача при выстреле из орудия. | На принципе отдачи основано реактивное движение. В ракете при сгорании топлива газы, нагретые до высокой температуры, выбрасываются из сопла с большой скоростью  относительно ракеты. Обозначим массу выброшенных газов через m, а массу ракеты после истечения газов через M. относительно ракеты. Обозначим массу выброшенных газов через m, а массу ракеты после истечения газов через M. | ||||
Тогда для замкнутой системы «ракета + газы» можно записать на основании закона сохранения импульса (по аналогии с задачей о выстреле из орудия):
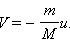 | (1.6) |
где V – скорость ракеты после истечения газов. Здесь предполагалось, что начальная скорость ракеты равнялась нулю.
Полученная формула для скорости ракеты справедлива лишь при условии, что вся масса сгоревшего топлива выбрасывается из ракеты одновременно. На самом деле истечение происходит постепенно в течение всего времени ускоренного движения ракеты. Каждая последующая порция газа выбрасывается из ракеты, которая уже приобрела некоторую скорость.
Для получения точной формулы процесс истечения газа из сопла ракеты нужно рассмотреть более детально. Пусть ракета в момент времени t имеет массу M и движется со скоростью 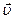 (рис. 1.5 (1)). В течение малого промежутка времени Δt из ракеты будет выброшена некоторая порция газа с относительной скоростью
(рис. 1.5 (1)). В течение малого промежутка времени Δt из ракеты будет выброшена некоторая порция газа с относительной скоростью  . Ракета в момент t + Δt будет иметь скорость
. Ракета в момент t + Δt будет иметь скорость  , а ее масса станет равной M + ΔM, где ΔM < 0 (рис. 1.5 (2)). Масса выброшенных газов будет, очевидно, равна –ΔM > 0. Скорость газов в инерциальной системе OX будет равна
, а ее масса станет равной M + ΔM, где ΔM < 0 (рис. 1.5 (2)). Масса выброшенных газов будет, очевидно, равна –ΔM > 0. Скорость газов в инерциальной системе OX будет равна 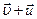 . Применим закон сохранения импульса. В момент времени t + Δt импульс ракеты равен
. Применим закон сохранения импульса. В момент времени t + Δt импульс ракеты равен  , а импульс испущенных газов равен
, а импульс испущенных газов равен  . В момент времени t импульс всей системы был равен
. В момент времени t импульс всей системы был равен  . Предполагая систему «ракета + газы» замкнутой, можно записать:
. Предполагая систему «ракета + газы» замкнутой, можно записать:
 | (1.7) |
Величиной  можно пренебречь, так как |ΔM| << M. Разделив обе части последнего соотношения на Δt и перейдя к пределу при Δt → 0, получим
можно пренебречь, так как |ΔM| << M. Разделив обе части последнего соотношения на Δt и перейдя к пределу при Δt → 0, получим
 | (1.8) | ||||
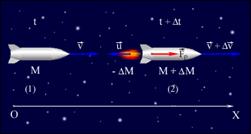 Рис. 1.5. Ракета, движущаяся в свободном пространстве (без гравитации). 1 – в момент времени t. Масса ракеты М, ее скорость Рис. 1.5. Ракета, движущаяся в свободном пространстве (без гравитации). 1 – в момент времени t. Масса ракеты М, ее скорость 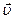 . 2 – Ракета в момент времени t + Δt. Масса ракеты M + ΔM, где ΔM < 0, ее скорость . 2 – Ракета в момент времени t + Δt. Масса ракеты M + ΔM, где ΔM < 0, ее скорость  масса выброшенных газов –ΔM > 0, относительная скорость газов масса выброшенных газов –ΔM > 0, относительная скорость газов  , скорость газов в инерциальной системе , скорость газов в инерциальной системе 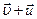 . . | Величина  есть расход топлива в единицу времени. Величина есть расход топлива в единицу времени. Величина  называется реактивной силой тяги называется реактивной силой тяги  .Реактивная сила тяги действует на ракету со стороны истекающих газов, она направлена в сторону, противоположную относительной скорости. Соотношение .Реактивная сила тяги действует на ракету со стороны истекающих газов, она направлена в сторону, противоположную относительной скорости. Соотношение  выражает второй закон Ньютона для тела переменной массы. Если газы выбрасываются из сопла ракеты строго назад выражает второй закон Ньютона для тела переменной массы. Если газы выбрасываются из сопла ракеты строго назад | ||||
(рис. 1.5), то в скалярной форме это соотношение принимает вид: Ma = μu,
где u – модуль относительной скорости. С помощью математической операции интегрирования из этого соотношения можно получить формулу для конечной скорости υ ракеты:
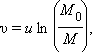 | (1.9) |
где  – отношение начальной и конечной масс ракеты. Эта формула называется формулой Циолковского. Из нее следует, что конечная скорость ракеты может превышать относительную скорость истечения газов. Следовательно, ракета может быть разогнана до больших скоростей, необходимых для космических полетов. Но это может быть достигнуто только путем расхода значительной массы топлива, составляющей большую долю первоначальной массы ракеты. Например, для достижения первой космической скорости υ = υ1 = 7,9·103 м/с при u = 3·103 м/с (скорости истечения газов при сгорании топлива бывают порядка 2–4 км/с) стартовая масса одноступенчатой ракеты должна примерно в 14 раз превышать конечную массу. Для достижения конечной скорости υ = 4u отношение
– отношение начальной и конечной масс ракеты. Эта формула называется формулой Циолковского. Из нее следует, что конечная скорость ракеты может превышать относительную скорость истечения газов. Следовательно, ракета может быть разогнана до больших скоростей, необходимых для космических полетов. Но это может быть достигнуто только путем расхода значительной массы топлива, составляющей большую долю первоначальной массы ракеты. Например, для достижения первой космической скорости υ = υ1 = 7,9·103 м/с при u = 3·103 м/с (скорости истечения газов при сгорании топлива бывают порядка 2–4 км/с) стартовая масса одноступенчатой ракеты должна примерно в 14 раз превышать конечную массу. Для достижения конечной скорости υ = 4u отношение  должно быть равно 50.
должно быть равно 50.
Изучите модель «Реактивное движение».
 Модель. Реактивное движение. Модель. Реактивное движение. | Модель предназначена для иллюстрации закона сохранения импульса на примере реактивного движения. Демонстрируется движение ракеты в свободном пространстве. Приводится график изменения скорости движения ракеты во времени. Относительная скорость u истечения газов из ракеты предполагается заданной. Изменяя массу топлива Mт, заправленного в ракету, можно наблюдать ускоренное движение ракеты до момента полного выгорания топлива и ее последующее равномерное движение. Попробуйте определить в компьютерном эксперименте, при каком минимальном отношении начальной и конечной масс  одноступенчатой ракеты она может достичь первой космической скорости (при заданной скорости истечения газов). Проверьте результат с помощью формулы Циолковского. одноступенчатой ракеты она может достичь первой космической скорости (при заданной скорости истечения газов). Проверьте результат с помощью формулы Циолковского. |
Значительное снижение стартовой массы ракеты может быть достигнуто при использовании многоступенчатых ракет, когда ступени ракеты отделяются по мере выгорания топлива. Из процесса последующего разгона ракеты исключаются массы контейнеров, в которых находилось топливо, отработавшие двигатели, системы управления и т. д. Именно по пути создания экономичных многоступенчатых ракет развивается современное ракетостроение.
Энергетические характеристики движения вводятся на основе понятия механической работы или работы силы.
Работой A, совершаемой постоянной силой 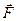 , называется физическая величина, равная произведению модулей силы и перемещения, умноженному на косинус угла α между векторами силы
, называется физическая величина, равная произведению модулей силы и перемещения, умноженному на косинус угла α между векторами силы 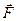 и перемещения
и перемещения  (рис. 1.6):
(рис. 1.6):
| A = Fs cos α.. | (1.10) |
Работа является скалярной величиной. Она может быть как положительна (0° ≤ α < 90°), так и отрицательна (90° < α ≤ 180°). При α = 90° работа, совершаемая силой, равна нулю. В системе СИ работа измеряется в джоулях (Дж).
Джоуль равен работе, совершаемой силой в 1 Н на перемещении 1 м в направлении действия силы.
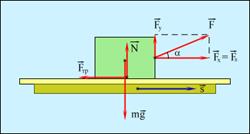 Рис. 1.6. Работа силы Рис. 1.6. Работа силы  . . | Если проекция  силы силы 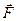 на направление перемещения на направление перемещения 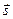 не остается постоянной, работу следует вычислять для малых перемещений Δsi и суммировать результаты: не остается постоянной, работу следует вычислять для малых перемещений Δsi и суммировать результаты:  . . |
Эта сумма в пределе (Δsi → 0) переходит в интеграл.
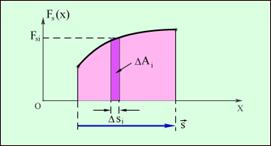 Рис. 1.7. Графическое определение работы. ΔAi = FsiΔsi. Рис. 1.7. Графическое определение работы. ΔAi = FsiΔsi. | Графически работа определяется по площади криволинейной фигуры под графиком Fs(x) (рис. 1.7). Если к телу приложено несколько сил, то общая работа всех сил равна алгебраической сумме работ, совершаемых отдельными силами и равна работе равнодействующей приложенных сил. |
Работа силы, совершаемая в единицу времени, называется мощностью. Мощность N это физическая величина, равная отношению работы A к промежутку времени t, в течение которого совершена эта работа:
| (1.11) |
В Международной системе (СИ) единица мощности называется ватт (Вт). Ватт равен мощности силы, совершающей работу в 1 Дж за время 1 с.
 |
Изучите модель «Механическая работа».
 Модель. Механическая работа. Модель. Механическая работа. | В модели иллюстрируется понятие механической работы на примере движения бруска на плоскости с трением под действием внешней силы, направленной под некоторым углом к горизонту. Изменяя параметры модели (массу бруска m, коэффициент трения μ, модуль и направление действующей силы 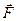 ), можно проследить за величиной работы, совершаемой при движении бруска, силой трения и внешней силой. Убедитесь в компьютерном эксперименте, что сумма этих работ равна кинетической энергии бруска. Обратите внимание, что работа силы трения Aтр всегда отрицательна. ), можно проследить за величиной работы, совершаемой при движении бруска, силой трения и внешней силой. Убедитесь в компьютерном эксперименте, что сумма этих работ равна кинетической энергии бруска. Обратите внимание, что работа силы трения Aтр всегда отрицательна. |
 Рис. 1.8. Работа равнодействующей силы.. A = F1s cos α1 + F2s cos α2 = F1ss + F2ss = = Fрss = Fрs cos α. Рис. 1.8. Работа равнодействующей силы.. A = F1s cos α1 + F2s cos α2 = F1ss + F2ss = = Fрss = Fрs cos α. | Если тело некоторой массы m двигалось под действием приложенных сил, и его скорость изменилась от  до до 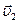 , то силы совершили определенную работу A. Работа всех приложенных сил равна работе равнодействующей силы (рис. 1.8). Между изменением скорости тела и работой, совершенной приложенными к телу силами, существует связь. , то силы совершили определенную работу A. Работа всех приложенных сил равна работе равнодействующей силы (рис. 1.8). Между изменением скорости тела и работой, совершенной приложенными к телу силами, существует связь. |
Эту связь проще всего установить, рассматривая движение тела вдоль прямой линии под действием постоянной силы 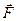 .
.
В этом случае векторы силы 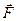 , перемещения
, перемещения 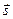 , скорости
, скорости 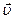 и ускорения
и ускорения 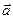 направлены вдоль одной прямой, и тело совершает прямолинейное равноускоренное движение. Направив координатную ось вдоль прямой движения, можно рассматривать F, s, υ и a как алгебраические величины (положительные или отрицательные в зависимости от направления соответствующего вектора). Тогда работу силы можно записать как A = Fs. При равноускоренном движении перемещение s выражается формулой
направлены вдоль одной прямой, и тело совершает прямолинейное равноускоренное движение. Направив координатную ось вдоль прямой движения, можно рассматривать F, s, υ и a как алгебраические величины (положительные или отрицательные в зависимости от направления соответствующего вектора). Тогда работу силы можно записать как A = Fs. При равноускоренном движении перемещение s выражается формулой
 |
Отсюда следует, что
 |
Это выражение показывает, что работа, совершенная силой (или равнодействующей всех сил), связана с изменением квадрата скорости (а не самой скорости).
Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела:
 | (1.12) |
Работа приложенной к телу равнодействующей силы равна изменению его кинетической энергии.
| A = Ek2 – Еk1. | (1.13) |
Это утверждение называют теоремой о кинетической энергии. Теорема о кинетической энергии справедлива и в общем случае, когда тело движется под действием изменяющейся силы, направление которой не совпадает с направлением перемещения.
Кинетическая энергия – это энергия движения. Кинетическая энергия тела массой m, движущегося со скоростью 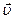 , равна работе, которую должна совершить сила, приложенная к покоящемуся телу, чтобы сообщить ему эту скорость:
, равна работе, которую должна совершить сила, приложенная к покоящемуся телу, чтобы сообщить ему эту скорость:
 | (1.14) |
Если тело движется со скоростью 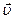 , то для его полной остановки необходимо совершить работу
, то для его полной остановки необходимо совершить работу
 | (1.15) |
Наряду с кинетической энергией или энергией движения в физике важную роль играет понятие потенциальной энергии или энергии взаимодействия тел.
Потенциальная энергия определяется взаимным положением тел (например, положением тела относительно поверхности Земли). Понятие потенциальной энергии можно ввести только для сил, работа которых не зависит от траектории движения тела и определяется только начальным и конечным положениями. Такие силы называются консервативными.
Работа консервативных сил на замкнутой траектории равна нулю. Это утверждение поясняет рис. 1.9.
Свойством консервативности обладают сила тяжести и сила упругости. Для этих сил можно ввести понятие потенциальной энергии.
 Рис. 1.9. Работа консервативной силы A1a2 = A1b2. Работа на замкнутой траектории A = A1a2 + A2b1 = A1a2 – A1b2 = 0. Рис. 1.9. Работа консервативной силы A1a2 = A1b2. Работа на замкнутой траектории A = A1a2 + A2b1 = A1a2 – A1b2 = 0. | Если тело перемещается вблизи поверхности Земли, то на него действует постоянная по величине и направлению сила тяжести  . Работа этой силы зависит только от вертикального перемещения тела. На любом участке пути работу силы тяжести можно записать в проекциях вектора перемещения . Работа этой силы зависит только от вертикального перемещения тела. На любом участке пути работу силы тяжести можно записать в проекциях вектора перемещения 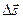 на ось OY, направленную вертикально на ось OY, направленную вертикально |
вверх: ΔA = FтΔs cos α = –mgΔsy,
где Fт = Fтy = –mg – проекция силы тяжести, Δsy – проекция вектора перемещения. При подъеме тела вверх сила тяжести совершает отрицательную работу, так как Δsy > 0. Если тело переместилось из точки, расположенной на высоте h1, в точку, расположенную на высоте h2 от начала координатной оси OY (рис. 1.10), то сила тяжести совершила работу
| A = –mg(h2 – h1) = –(mgh2 – mgh1). | (1.16) | ||||
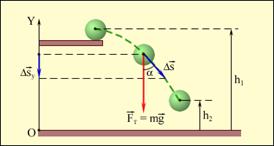 Рис. 1.10. Работа силы тяжести. Рис. 1.10. Работа силы тяжести. | Эта работа равна изменению некоторой физической величины mgh, взятому с противоположным знаком. Эту физическую величину называют потенциальной энергией тела в поле силы тяжести Ep = mgh. Она равна работе, которую совершает сила тяжести при опускании тела на нулевой | ||||
уровень.
Работа силы тяжести равна изменению потенциальной энергии тела, взятому с противоположным знаком.
| A = –(Ep2 – Ep1). | (1.17) |
Потенциальная энергия Ep зависит от выбора нулевого уровня, т. е. от выбора начала координат оси OY. Физический смысл имеет не сама потенциальная энергия, а ее изменение ΔEp = Ep2 – Ep1 при перемещении тела из одного положения в другое. Это изменение не зависит от выбора нулевого уровня.
Если рассматривать движение тел в поле тяготения Земли на значительных расстояниях от нее, то при определении потенциальной энергии необходимо принимать во внимание зависимость силы тяготения от расстояния до центра Земли (закон всемирного тяготения). Для сил всемирного тяготения потенциальную энергию удобно отсчитывать от бесконечно удаленной точки, т. е. полагать потенциальную энергию тела в бесконечно удаленной точке равной нулю. Формула, выражающая потенциальную энергию тела массой m на расстоянии r от центра Земли, имеет вид:
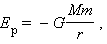 | (1.18) |
где M – масса Земли, G – гравитационная постоянная.
Изучите модель «Кинетическая и потенциальная энергии».
 | В модели демонстрируется изменение кинетической Ek и потенциальной Ep энергии мальчика, спускающегося на санках без трения с горы сложного профиля. Показывается диаграмма и выводятся численные значения кинетической и потенциальной энергии. Можно изменять массу мальчика m и профиль горы. Обратите внимание, что сумма потенциальной и кинетической энергии в процессе движения мальчика постоянна и равна первоначальной потенциальной энергии до старта с вершины горы. |
| Модель. Кинетическая и потенциальная энергия. |
Понятие потенциальной энергии можно ввести и для упругой силы. Эта сила также обладает свойством консервативности. Растягивая (или сжимая) пружину, мы можем делать это различными способами.
Можно просто удлинить пружину на величину x, или сначала удлинить ее на 2x, а затем уменьшить удлинение до значения x и т. д. Во всех этих случаях упругая сила совершает одну и ту же работу, которая зависит только от удлинения пружины x в конечном состоянии, если первоначально пружина была недеформирована. Эта работа равна работе внешней силы A, взятой с противоположным знаком:
 | (1.19) |
где k – жесткость пружины. Растянутая (или сжатая) пружина способна привести в движение, прикрепленное к ней тело, т. е. сообщить этому телу кинетическую энергию. Следовательно, такая пружина обладает запасом энергии. Потенциальной энергией пружины (или любого упруго деформированного тела) называют величину
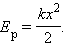 | (1.20) |
Потенциальная энергия упруго деформированного тела равна работе силы упругости при переходе из данного состояния в состояние с нулевой деформацией.
Если в начальном состоянии пружина уже была деформирована, а ее удлинение было равно x1, тогда при переходе в новое состояние с удлинением x2 сила упругости совершит работу, равную изменению потенциальной энергии, взятому с противоположным знаком:
 | (1.21) |
Потенциальная энергия при упругой деформации – это энергия взаимодействия отдельных частей тела между собой силами упругости.
Свойством консервативности обладают наряду с силой тяжести и силой упругости некоторые другие виды сил, например, сила электростатического взаимодействия между заряженными телами. Сила трения не обладает этим свойством. Работа силы трения зависит от пройденного пути. Понятие потенциальной энергии для силы трения вводить нельзя.
Если тела, составляющие замкнутую механическую систему, взаимодействуют между собой только силами тяготения и упругости, то работа этих сил равна изменению потенциальной энергии тел, взятому с противоположным знаком:
| A = –(Ep2 – Ep1). | (1.22) |
По теореме о кинетической энергии эта работа равна изменению кинетической энергии тел:
| A = Ek2 – Ek1. | (1.23) |
Следовательно Ek2 – Ek1 = –(Ep2 – Ep1) или
| Ek1 + Ep1 = Ek2 + Ep2. | (1.24) |
Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой силами тяготения и силами упругости, остается неизменной.
Это утверждение выражает закон сохранения энергии в механических процессах. Он является следствием законов Ньютона. Сумму E = Ek + Ep называют полной механической энергией. Закон сохранения механической энергии выполняется только тогда, когда тела в замкнутой системе взаимодействуют между собой консервативными силами, то есть силами, для которых можно ввести понятие потенциальной энергии.
Пример применения закона сохранения энергии – нахождение минимальной прочности легкой нерастяжимой нити, удерживающей тело массой m при его вращении в вертикальной плоскости (задача Х. Гюйгенса). Рис. 1.20.1 поясняет решение этой задачи.

