Метод математической индукции

Слово индукция по-русски означает наведение, а индуктивными называют выводы, на основе наблюдений, опытов, т.е. полученные путем заключения от частного к общему. Например, мы каждый день наблюдаем, что Солнце восходит с востока. Поэтому можно быть уверенным, что и завтра оно появится на востоке, а не на западе. Этот вывод мы делаем, не прибегая ни к каким предположениям о причине движения Солнца по небу (более того, само это движение оказывается кажущимся,поскольку на самом деле движется земной шар).

Суть метода математической индукции. Во многих разделах арифметики, алгебры, геометрии, анализа приходится доказывать истинность предложений А(n), зависящих от натуральной переменной. Доказательство истинности предложения А(n) для всех значений переменной часто удается провести методом математической индукции, который основан наследующем принципе.

Предложение А(n) считается истинным для всех натуральных значений переменной, если выполнены следующие два условия:

1. Предложение А(n) истинно для n=1.

2. Из предположения, что А(n) истинно для n=k (где k – любое натуральное число), следует, что оно истинно и для следующего значения n=k+1.

Этот принцип называется принципом математической индукции. Обычно он выбирается в качестве одной из аксиом, определяющих натуральный ряд чисел, и, следовательно, принимается без доказательства. Под методом математической индукции понимают следующий способ доказательства.

Если требуется доказать истинность предложения А(n) для всех натуральных n,то, во-первых, следует проверить истинность высказывания А(1) и, во-вторых, предположив истинность высказывания А(k), попытаться доказать, что высказывание А(k+1) истинно. Если это удается доказать, причем доказательство

остается справедливым для каждого натурального значения k, то в соответствии с принципом математической индукции предложение А(n) признается истинным для всех значений n. Метод математической индукции широко применяется при доказательстве теорем, тождеств, неравенств, при решении задач на делимость, при решении некоторых геометрических и многих других задач.

Бином Ньютона.

Дальше будет получена формула бинома Ньютона с помощью приемов дифференциального исчисления. Бином Ньютона – это формула, выражающая выражение (a + b)ⁿ в виде многочлена. Эта формула имеет вид:

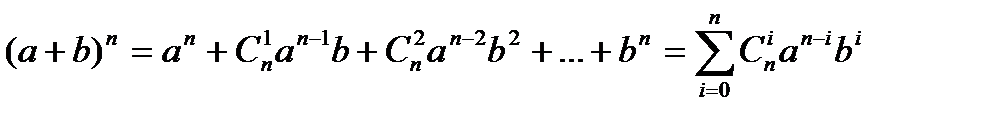
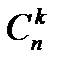- число сочетаний из п элементов по k.

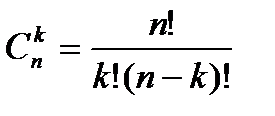
Широко известные формулы сокращенного умножения квадрата суммы и разности, куба суммы и разности, являются частными случаями бинома Ньютона. Когда степень бинома невысока, коэффициенты многочлена могут быть найдены не расчетом по формуле количества сочетаний, а с помощью так называемого треугольника Паскаля. Этот треугольник имеет вид:

1 2 1

1 3 3 1

1 4 6 4 1

1 5 10 10 5 1

…………………

Формула бинома Ньютона может быть обобщена для произвольного числа слагаемых.

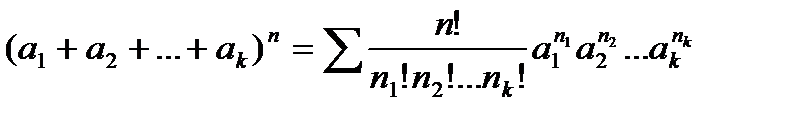
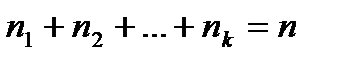
При вычислениях 0! принимается равным 1.