Геометрический смысл АФЛ. Приближенные формулы

БАКАЛАВРЕАТ-1

Конспекты лекций за 1 семестр, 2011 года.

1. Числовые множества. Натуральные числа N, целые Z, рациональные Q (m / n или периодические десятичные дроби), иррациональные (¹ m/n или непериодические дроби), действительные R. Числовая ось. Модуль и его свойства: |a±b|£|a|+|b|, |ab|=|a||b|, |a/b|=|a|/|b|. Геометрический смысл величины |x₁ – x₂|. Промежутки [a,b], (a,b], (–¥, b], (a,+¥) и т.д. Окрестность конечной точки, её центр и радиус, обозначение 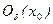. Проколотая окрестность. Окрестности бесконечностей – ¥, +¥, ¥.

Определение окрестностей через неравенства с модулем и без. Изображение промежутков и окрестностей на числовой оси (пустые или закрашенные точки; квадратные или круглые скобки).

2. Числовые функции. Говорят, что задана функция, если каждому значению хÎD соответствует единственное число у; множество D называется областью определения функции. Множество значений функции называется областью изменения Е.

Итак, функция = область определения + закон соответствия. Если область определения не указана, то подразумевается, что она совпадает с ОДЗ. Три способа задания функции. (Сомнительность графического способа (толщина линии)!)

Графиком функции называется множество точек плоскости, координаты которых (х,у) удовлетворяют условиям {xÎD, y = f(x)}.

Элементарные ф-ии :

.

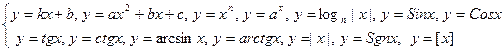3. Элементарные свойства функций:

а) Знак (график выше оси Х, ниже оси Х), нули функции, точки пересечения с осью Y.

б) Монотонность наглядно – «в гору», «под гору» (любые две точки на кривой удовлетворяют условию выше-ниже). Строгое определение функции, монотонной на множестве М. Пример. у=1/х не является монотонной на области определения!!!

в) Ограниченность на множестве М (сверху, снизу, просто), геометрический смысл, точное определение. Кванторы ", $, определение ограниченности, отрицание этого определения.

ТЕОРЕМА. Сумма и произведение ограниченных на М функций также ограничены на этом множестве. ДОК-ВО.

Вопрос: верно ли это для частного двух ограниченных на М функций? ( tgx = Sinx/Сosx).

Вопрос: Почему y = Sinx , y = x² ограничены снизу на R, а их произведение – нет.

г) Периодичность, определение и примеры. 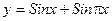не является периодической.

д) Обратная функция. Определение: Пусть дана функция y = f(x), xÎD, yÎE и пусть уравнение f(x) = y имеет единственное решение x = g(y) для любого yÎE . Тогда эта зависимость называется обратной функцией для функции y = f(x), xÎD, yÎE. Основные тождества. Графики взаимно обратных функций – это одна и та же кривая!

Не всякая функция имеет обратную.

ТЕОРЕМА. Всякая монотонная функция имеет обратную. Объяснение на графике.

ЗАДАЧА. Привести пример немонотонной функции, имеющей обратную.

4. Пределы функций.

Процессы на оси Х: x® x₀–0 , x® x₀+0 , x® –¥ , x®+¥ . (Изобразить на оси Х точки со стрелочками, процессы изображать движением рук). Возможны также случаи х® х₀ и х ® ¥ . Пример. х=(–1)^пп

Аналогично процессы на оси Y: y=f(x)® b , –¥ , +¥ .

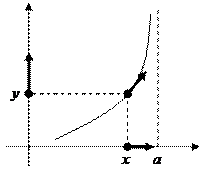
Графическое определение пределов функции.

Пример. Дать графическое определение предела

.

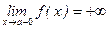Изображается кривая, три точки (на оси Х, на оси Y и на кривой) и три стрелки, соответствующие процессам.

Аналогичным образом определяются другие типы пределов.

Примечание. Процесс х® а означает, что х может стремится к а как справа так и слева; процесс х® ¥ означает, что х может стремится как к +¥ так и к –¥ .

Способы вычисления простеньких пределов: а)Подстановка, б)сокращение и подстановка, в)деление на старшую степень при х® ¥.

Замечание. Переменная, по которой вычисляется предел, может быть любой буквой.

ОЧЕВИДНЫЕ арифметические свойства пределов (линейность операции lim, предел произведения, частного).

5. Бесконечно малые и бесконечно большие функции и их свойства.

Определение (предел равен 0 или ¥), примеры (графические и аналитические). Обязательное указание процесса.

Степенные, показательные, логарифмические бесконечности.

ТЕОРЕМЫ о связи б.м. и б.б. функций. без д-ва, человеческое обоснование (если одно яблоко поделить на 1000 человек, сколько получит каждый?).

ТЕОРЕМА о сумме б.м. и о произведении б.м. на ограниченную. Без д-ва.

ТЕОРЕМА О связи конечного предела с б.м. функцией. f(x)®AÛf(x)=A+a(x). Без д-ва. Пример вычисления предела при х® ¥ : 2+б.м.

6. Сравнение бесконечно малых и бесконечно больших величин.

Житейский пример. Пусть две положительных величины таковы, что m/n = 0,001. Какая из этих величин меньше и во сколько раз? Аналогичный вопрос для a/b=1000.

Сравнения б.м. и б.б. функций. Определение по аналогии соотношений

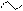
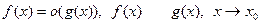. (для запоминания: f(x) – Очень МАЛАЯ по сравнению с g(x) в данном процессе)

Примеры. Сравнить величины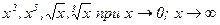

Важное определение: .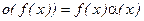

Из него вытекает: !!!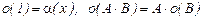

Шкала бесконечностей.

Из графика видно, что . Используя это, найдем

ТЕОРЕМА о замене сомножителя ненулевой константой. Если f(x)® А ¹ 0 при х® х₀ , то f(x)g(x)~Ag(x) при х® х₀ . Д-во.

ТЕОРЕМА о сохранении главного слагаемого. f(x) + o(f(x)) ~ f(x). Д-во.

ПРИМЕЧАНИЕ. Сохранение главного слагаемого под знаком функции недопустимо для показательных функций, т.е. exp( f(x) + o(f(x)) ) не всегда ~ exp( f(x)) !!!!!!!

Определение. Если f(x) = g(x) + o(g(x)) при х®х₀ , то функция g(x) называется главной частью функции f(x) (или её асимптотикой) при х® х₀ (или её асимптотикой в точке х₀).

Пример. Найти асимптотики в нулях, в особых точках и на бесконечности для функций.

. Чему равен y при x = 1000 ?

Построить эскизы графиков по этим асимптотикам.

7. Свойства функций, имеющих конечный предел.

ТЕОРЕМА. Функция, имеющая конечный предел в некотором процессе, ограничена в этом процессе, т.е в некоторой (проколотой) окрестности предельной точки.

Без доказательства. Демонстрация на примере f(x)®2 при x® - ¥

ТЕОРЕМА. Если неотрицательная в некотором процессе функция имеет предел в этом процессе, то этот предел неотрицателен.

Без доказательства, с графической иллюстрацией.

Контрпример для ПОЛОЖИТЕЛЬНЫХ функций.

Следствие. Переход к пределу в неравенствах.

Д-во с использованием предыдущей теоремы

ТЕОРЕМА. Если предел функции положителен, то и сама функция положительна, начиная с некоторого момента процесса. Графическая иллюстрация.

ТЕОРЕМА о двух милиционерах. Формулировка и графическая иллюстрация

Первый замечательный предел. 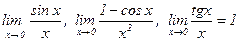. Всё с выводом.

Второй замечательный предел 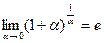. (без вывода).

Использование второго замечательного предела для вывода следствий

Следствия.

8. Асимптотические формулы.

Напомнить соотношения: 1)

2) f(x)×a(x)=o(f(x)) , x ® x₀ .

При х ® 0 имеют место формулы (некоторые с выводом):

Sinx = x+ o(x), Cosx = 1+ x²/2 + o(x² ), tgx = x + o(x),

ln(1+x) = x + o(x), e^x = 1 + x + o(x), (1 + x)ⁿ = 1+nx+o(x) .

9. Непрерывные функции.

Определение. Функция y = f(x) называется непрерывной в точке х₀ , если

а) она определена в некоторой окрестности этой точки,

б) $

Непрерывность СПРАВА и СЛЕВА. Не давать строгие определения. Лучше всё показать на картинках

Вывод. Для непрерывной функции предел вычисляется подстановкой:

.

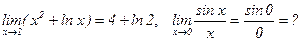Дать определение «приращения в точке». Примеры. Геометрический смысл.

Печальный опыт. Больше половины публики не может найти Dу для у=1/х .

Другое определение непрерывности: Бесконечно малому Dх соответствует бесконечно малое Dу .

Геометрический смысл непрерывности функции: График рисуется, не отрывая руки от бумаги.

Тонкость: не является непрерывной в нуле! (Она непрерывна справа).

10. Основные теоремы о непрерывных функциях.

ТЕОРЕМА о локальной ограниченности. Д-во. Нарисуйте график функции, которая непрерывна в точке х=2. Покажите, что функция ограничена в некоторой окрестности этой точки (график между двумя горизонталями)

ТЕОРЕМА о сохранении знака непрерывной функции. Д-во. Нарисуйте график функции, которая непрерывна в точке х=2. и f(2)>0. Покажите, что f(x)>0 также и в некоторой окрестности точки х=2.

ТЕОРЕМЫ об арифметических операциях с непрерывными функциями. Сформулировать и предупредить, что для частного непрерывных функций имеются оговорки.

11 Сложная функция. Непрерывность.

Определение. Пусть каждому х из множества D соответствует единственное z из Е (задана z=g(x) на множестве D), а каждому z из Е соответствует единственное y (задана y = f(z) на множестве Е). Это означает, что задана сложная функция y=f(g(x)), xÎD. Функция f( ) – внешняя, функция g( ) – внутренняя.

Условие существования: Внешняя функция должна быть определена на множестве значений внутренней функции: сложная функция y = ln(–x²) не существует.

Сложная функция называется также суперпозицией.

ТЕОРЕМА о непрерывности сложной функции. Пусть задана сложная функция y = f(g(x)) и пусть внутренняя функция z=g(x) непрерывна в точке х₀ , а внешняя функция f(z) непрерывна в соответствующей точке z₀ = g(x₀). Тогда сложная функция будет непрерывной в точке х₀ .

ОБОСНОВАНИЕ. Дадим х малое приращение Dх. Тогда функция z=g(x) получит малое (в силу непрерывности g(x)) приращение Dz. А тогда функция y=f(z) получит малое (в силу непрерывности f(z)) приращение Dу. Следовательно, малому приращению Dх соответствует малое приращение Dу сложной функции y=f(g(x)) , а это означает, что сложная функция непрерывна.

12. Обратная функция. Непрерывность.

Определение обратной функции как решения уравнения y = f(x) относительно х.

Основные тождества для взаимно обратных функций.

Графики взаимно обратных функций – это одна и та же кривая.

ТЕОРЕМА о непрерывности обратной функции. Пусть y = f(x) строго монотонна и непрерывна на (а, b). Тогда у этой функции существует обратная функция, и эта обратная функция является непрерывна.

Д-во крестьянское: 1) существование, т.к. строгая монотонность, 2) непрерывность, т.к. графики взаимообратных функций это одна и та же кривая. Их оба можно нарисовать не отрывая карандаша от бумаги.

13. Непрерывность элементарных функций.

6) Напомнить графики линейной функции, экспоненты и показательной функции, тригонометрических функций. «А теперь самостоятельно напишите: Функция такая-то непрерывна там-то». Рассмотреть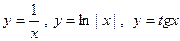

14. Классификация точек разрыва. (Обязательно картинки!!!)

НАПОМИНАНИЕ. Если функция y=f(x) непрерывна в точке х=а , то существуют односторонние пределы и они равны f(a).

ОПРЕДЕЛЕНИЕ. Точка х=а называется точкой устранимого разрыва, если односторонние пределы в этой точке существуют и равны, а значение функции в этой точке не совпадает со значением этих пределов либо функция вообще не определена при х=а.

Примеры. y=sgn²(x) ; .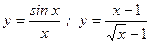

Обсуждение. Почему разрыв называется устранимым.

ОПРЕДЕЛЕНИЕ. Точка х=а называется точкой разрыва первого рода (скачком), если односторонние пределы существуют и различны. В самой точке функция может быть либо определена, либо не определена.

Примеры. y=sgn(x) ,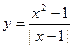

(Кусочно-заданная функция, >f:=x–>piecewise(x<1,1-x,x-1); )

ОПРЕДЕЛЕНИЕ. Точка х=а называется точкой разрыва второго рода, если хотя бы один из односторонних пределов не существует.

Примеры. .

.Мнемоническое правило. Разрыв 1-го рода МАЛЕНЬКИЙ, 2-го рода БОЛЬШОЙ (2>1).

15. Функции непрерывные на отрезке.

ОПРЕДЕЛЕНИЕ. Пусть функция определена в правой полуокрестности точки а и пусть 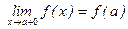. Тогда функция называется непрерывной в точке х=а справа. Аналогичное определение непрерывности в точке слева.

Примеры: , ,

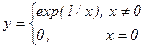ОПРЕДЕЛЕНИЕ. Функции y=f(x) называется непрерывной на отрезке [a, b], если её график, соединяющий точки (a,f(a)) и (b,f(b)) можно нарисовать, не отрывая карандаша от бумаги. Задача. Нарисовать график функции, непрерывной на отрезке [–1, 3].

Свойства функций, непрерывных на отрезке.

Ø Теорема Коши о промежуточном значении. Пусть функция y=f(x) непрерывна на [a,b] и принимает на концах отрезка значения разных знаков. Тогда существует сÎ(a,b) такая, что f( c) = 0. Задача. Нарисовать такую функцию и найти точку х=с. Сколько таких точек может быть?

Примеры аналитические и графические.

Контрпримеры: у=1/(х–2) на [1;3] , у= sgnx–0,5 на [0; 1]

Ø 1-я теорема ВЕЙЕРШТРАССА. Если функция f(x) непрерывна на отрезке [a,b], то она ограничена на этом отрезке. Самостоятельно убедиться на графике.

Примеры и контрпримеры. а) нет отрезка, б) нет непрерывности

Ø 2-я теорема ВЕЙЕРШТРАССА. Если функция y=f(x) непрерывна на [a,b], то она достигает на этом отрезке свои max u min. Самостоятельно убедиться на графике.

Примеры и контрпримеры. y=Sgn(x)–x , на отрезке [–1; +1].

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ

ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ.

Определение производной. Пусть функция y=f(x) определена в некоторой окрестности точки х₀.

а) Составим приращение функции в этой точке Dy=f(x₀+Dx)–f(x₀).

б) Поделим это приращение на Dх.

в) Найдем предел отношения Dу/Dх при Dх® 0.

Если этот предел существует, то он называется производной функции f(x) в точке х₀. и обозначается через f’(x₀).

Итак, по определению

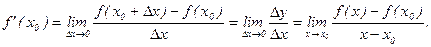
Определение. Функция y=f(x) наз. дифференцируемой в точке х₀, если существует f’(x₀).

Замечание. Из определения производной вытекает, что дифференцируемая в точке функция должна быть определена в некоторой окрестности этой точки.

*Механический смысл производной: S(t)– перемещение, V(t)=S’(t)– скорость.

Производные по определению (при наличии времени).

А) Производная от константы = 0.

В) Степенная функция у=х^п

…

С) Функции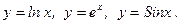

ТЕОРЕМА. Если функция y=f(x) дифференцируема в точке х₀ , то она непрерывна в этой точке.

Д-во: 1) Дифф Þ определена в некоторой окрестности точки х₀. (см. опр-е производной). 2) По условию существует предел от при Dх®0. Это означает, что Dy ®0 , т.к иначе предела не существовало бы. След. б/малому приращению по Х соответствует б/малое приращение по Y, т.е. функция непрерывна.

ОБРАТНАЯ ТЕОРЕМА неверна: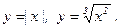

Уравнение касательной. Касательная – это прямая, положение которой определяется предельным положением секущей (рис.)

Вывод: .

• Кривая, имеющая в точке х₀ касательную, называется гладкой в этой точке.
• Дифференцируемая функция имеет гладкий график.
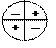• Гладкая кривая является непрерывной; но непрерывная кривая не обязательно гладкая (ломаная линия).

Геометрический смысл производной: Коэффициент при х , т.е. f’(x₀) - этотангенс угла наклона касательной к оси Х; знаки тангенса, знаки производной, возрастание и убывание функции.

Производные от суммы, произведения, частного.

Предварительные слова: Для любой функции

u(x+Dx) – u(x) = Du Þ u(x+Dx) = u(x) + Du.

ТЕОРЕМА. Пусть функции u(x), v(x) дифференцируемы в точке х. Тогда их сумма, произведение и частное также будут дифференцируемы в точке х, причем

(u+v)’=u’+v’, (uv)’=u’v+v’u, (u/v)’=(u’v–v’u)/v² .

В последнем случае предполагаем, что v(x)¹0 .

Д-во для суммы.

Пример применения: (tgx)’ , (ctgx)’ .

Производная от сложной функции y=f(z), где z=g(x).

Теорема. Пусть внутренняя функция z=g(x) дифференцируема в точке х₀ , а внешняя функция y=f(z) дифференцируема в соответствующей точке z₀=g(x₀). Тогда сложная функция y=f(g(x)) дифференцируема в точке х₀ и при этом производная в этой точке равна

y’=f’(z₀)×g’(x₀) .

Д-во: Дадим х₀ приращение Dх. Тогда внутренняя функция получит приращение Dz=g(x₀+Dx)–g(x₀), а внешняя функция получит приращение Dy=f(x₀+Dz)–f(z₀). Т.к. g(x) дифференцируема, то она непрерывна, и поэтому Dz®0 при Dx®0. Далее по определению

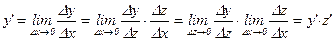= f’(z₀)×g’(x₀).

Предполагается без д-ва, что сложная функция определена в некоторой окрестности точки х₀ и что при стремлении Dx к нулю приращение Dz ® 0 , не обращаясь в нуль!

Примеры применения теоремы.

.

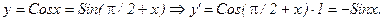
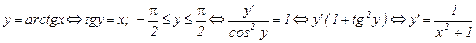Производная обратной функции. Теорема. Если функция у=у(х) дифференцируема в точке х₀, то обратная функция х=х(у) также является дифференцируемой в соответствующей точке у₀ и при этом y’(x₀)×x’(y₀)=1.

Д-во: Если прямая функция гладкая, то обратная функция также является гладкой, т.к. это одна и та же кривая (см. рис.). Согласно геометрическому смыслу производной

y’(x₀)=tga , x’(y₀)=tgb=tg(p/2-a)=ctga. .

Отсюда y’(x₀)× x’(y₀)= tga × ctga=1.

Линеаризация функции.

Теорема о линеаризации. Если функция y=f(x) дифференцируема в точке х₀ , то имеет место асимптотическая формула линеаризации (АФЛ)

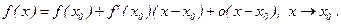
Д-во: По условию существует производная, т.е.

…

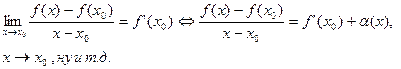Геометрический смысл АФЛ. Приближенные формулы

“Y” кривой = АС, “Y” касательной = АВ, ВС = о(х–х₀), х®х₀.

Линеаризация – это замена кривой на касательную или

замена функции f(x) на линейную функцию f(x₀)+f’(x₀)(x–x₀)

(отбрасываем о(x–x₀) ).

Пример: Приближенная формула

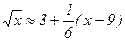, при х » 9, например, при х = 10.

Численное решение уравнения f(x) = 0. Метод касательных (метод Ньютона).

Пусть х₀ – приближенное решение уравнения. Проводим в этой точке линеаризацию и вместо уравнения f(x) = 0 решаем уравнение f(x₀)+f’(x₀))x–x₀)=0.

Вывод рекуррентной формулы метода Ньютона .

Геометрический смысл метода Ньютона.

Пример. f(x) = x² – 2 .

Дифференциал функции.

Определение. Пусть функция y=f(x) дифференцируема в точке х. Тогда дифференциалом функции y=f(x) на отрезке [x, x+Dx] называется величина dy=f’(x)Dx.

Примечание. Дифференциал зависит от двух величин – от х и от Dх .

Запись d(…)=(…)’Dx. Вписать в пустое место х² , х. Из последнего примера вытекает соотношение dx=Dx, а отсюда следует обозначение производной 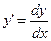(читается dy по dx). Геометрический смысл дифференциала – приращение ординаты при движении по касательной (см. рис.).

Запись АФЛ через дифференциал. Погрешность функции.

Пусть функция y=f(x) дифференцируема в точке х₀. Тогда имеет место АФЛ

f(x)=f(x₀)+f’(x₀)(x–x₀)+o(x–x₀), x–x₀ ®0.

Заменим всюду х на х₀+Dх. Получим

Dу = dy + o(Dx), Dx® 0 (см. рис.)

При малых Dx имеем Dy » dy.

Это равенство используется для приближенного вычисления погрешности функции.

Примеры.

Производные высших порядков.

Определение. Пусть функция у=f(x) дифференцируема на интервале (a,b). Тогда на этом интервале определена функция y=f’(x). Производная этой функции (если она существует) называется второй производной исходной функции и обозначается f’’(x).

Исследование поведения функции.

1. Определение локального экстремума (строгого и нестрогого).

2. Теорема Ферма. Пусть х₀ – точка экстремума функции y=f(x) и пусть f(x) дифференцируема в этой точке. Тогда f’(x₀)=0.

Доказательство: касательная в точке экстремума горизонтальна.

Обратная теорема неверна. Пример у = 4х³ – 3х⁴.

Определение критической точки. Либо f’(x₀)=0 либо производная в точке х₀ не

существует.

Теорема Ферма: ЭКСТР Þ КРИТ. ТОЧКА. Обратное неверно! (у=х³)

ЗАДАЧА ОБ ОЦЕНКЕ.

Пусть на отрезке [a, b] задана непрерывная функция y = f(x). Тогда по 1-й теореме Вейерштрасса она достигает на этом отрезке своё наибольшее и своё наименьшее значения, т.е. существуют числа x₁, x₂ Î [a, b] такие, что f(x₁)=m, f(x₂)=M и при этом имеет место двойное неравенство m £ f(x) £ M для любого х из отрезка [a, b]. Это двойное неравенство называется ТОЧНОЙ ОЦЕНКОЙ функции на отрезке.

Решение задачи о точной оценке. Пусть функция y = f(x) непрерывна на отрезке [a, b] и дифференцируема во всех внутренних точках отрезка. Наибольшее значение функция принимает или на границе или во внутренней точке, которая по теореме Ферма является в этом случае критической точкой. Аналогично, наименьшее значение может приниматься или на границе или в критической точке.

ПРАВИЛО. Найти критические точки х₁, х₂, х₃ функции, лежащие на отрезке [a, b] и из чисел f(a), f(x₁), f(x₂), f(x₃), f(b) выбрать наименьшее число m и наибольшее число M. Записать искомую оценку.

Пример. у = 3x⁴+4x³–12x², x Î [–1, 1] . Критические точки: –2 , 0 , 1

Значения f(–1)=–13; f(0)=0; f(1)=–5. m=–13, M=0. Следовательно, на отрезке [–1, 1] имеет место точная оценка функции: –13 £ f(x) £ 0.

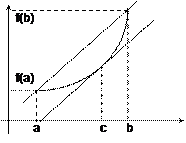
ТЕОРЕМА ЛАГРАНЖА ( о конечном приращении). Если f(x) непрерывна на [a,b] и дифференцируема на (a,b), то существует точка сÎ(a,b) такая, что приращение функции на отрезке имеет вид f(b)–f(a)=f’(c)(b–a).

Д-во: :Нарисовать непрерывную и гладкую линию, соединяющую точки A(a,f(a)) и B(b,f(b)). Найти на кривой точку х=с, в которой касательная параллельна хорде АВ. Углы наклона хорды и касательной одинаковы, и поэтому

.

откуда и получаем f(b)–f(a)=f’(c)(b–a). Словесная формулировка: «Разность значений функции равна разности значений аргумента на производную в средней точке».

Достаточное условие монотонности.

ТЕОРЕМА. Пусть f(x) дифференцируема (и, следовательно, непрерывна) на (a,b) и пусть её производная на этом интервале положительна (отрицательна). Тогда f(x) возрастает (убывает) на этом интервале.

Д-во: На любом [x₁,x₂]Ì(a,b) выполняются условия теоремы Лагранжа , и поэтому f(x₂)–f(x₁)=f’(c)(x₂–x₁). Отсюда видно, что знак левой части совпадает со знаком производной.

Достаточные условия экстремума по первой производной.

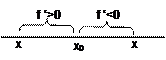ТЕОРЕМА. Пусть f(x) дифференцируема в некоторой окрестности критической точки х₀ и пусть в этой окрестности при переходе через точку х₀ производная меняет знак с плюса на минус (с минуса на плюс). Тогда точка х₀ является точкой максимума (минимума).

Д-во: для левой полуокрестности f(x₀)–f(x)=f’(c)(x₀–x)>0;

для правой полуокрестности f(x₀)–f(x)=f’(c)(x₀–x)>0;

Таким образом, всегда f(x₀)>f(x), т.е. имеем максимум.

Аналогично для минимума.

Пример. y= 6ln|x|+x² –8x.

Текстовые задачи на экстремум

1. В прямоугольный треугольник с катетами a , b вписать прямоугольник максимальной площади.

а) Выбираем параметр х (ширина прямоугольника).

б) Считая параметр известным, находим площадь прямоугольника как функцию от параметра х.

в) Исследуем эту функцию на экстремум.

2. На стене висит картина. Её нижний край выше глаза зрителя на a, верхний – на b. С какого расстояния эта картина видна под наибольшим углом.

3. Из круга вырезают сектор с углом А и изготавливают кулек в виде конуса. Какой должен быть угол А, чтобы объем кулька был максимальным. ( » 60⁰)

Методы раскрытия неопределённостей типа .

Напоминание: дроби 0/5 и 6/0 – не являются неопределённостями!!!

ПРАВИЛО ЛОПИТАЛЯ

Пусть f(x), g(x) дифференцируемы в точке х₀ и обращаются в этой точке в ноль, а производная g ‘(х₀ ) ¹ 0. Тогда

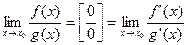
«Д-во»:

Примеры.

ПРАВИЛО ЛОПИТАЛЯ можно применять повторно

Примеры. .

Примечание 1. Правило Лопиталя применимо также в процессах х ® ± ¥.

Примечание 2. Правило Лопиталя применимо не только к неопределённостям типа , но и к неопределённостям типа .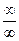

Примеры – шкала бесконечностей 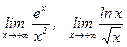. Найти эти пределы. Записать затем результаты с использованием «о-малого».

ФОРМУЛА ТЕЙЛОРА.

Определение. Пусть функция f(x) n раз дифференцируема в точке х₀. Тогда многочленом Тейлора n-го порядка для функции f(x) в точке х₀ называется многочлен

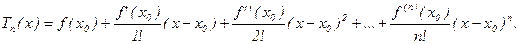
Примеры. f(x)=2x²+3x+4, х₀=1, записать Т₂(х). Вывод: Для многочлена Р_п(х)=Т_п(х). Для других функций это не так.

Пример. Sinx ≠ x – x³/6.

Основное свойство многочлена Тейлора:

В точке х=х₀ значения многочлена Тейлора и его первых n производных совпадают со значениями функции и её первых n производных.

Д-во: подстановкой и дифференцированием

ТЕОРЕМА ТЕЙЛОРА–ПЕАНО. Пусть функция f(x) n раз дифференцируема в О_d(х₀). Тогда для любого х из этой окрестности справедлива асимптотическая формула f(x)=T_n(x)+o((x-x₀)^п), x® x₀ .

Д-во: Нужно доказать, что 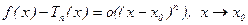или, что тоже самое,

Применим n раз правило Лопиталя (условия применимости правила Лопиталя выполнены!) и получаем то, что нужно доказать.

Пример

.

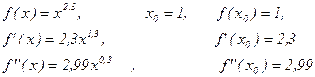
Формула Тейлора примет вид

Отбрасывая о-малое, получим приближенную формулу

Применение этой приближенной формулы 1,1^2,3 » 1+0,23+0,01495=1,24495 (точно=1,245097).

Формула МАКЛОРЕНА. Записать формулу Тейлора. Подставить в неё х₀=0.

.

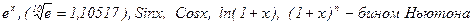. (точно ln3=1,09861)

Формула Тейлора –Пеано (Маклорена –Пеано) не дает возможности оценить остаточный член, т.е. оценить погрешность применения этой формулы.

ТЕОРЕМА ТЕЙЛОРА–ЛАГРАНЖА. Пусть функция 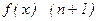раз дифференцируема в . Тогда для любого х из этой окрестности найдется сÎ (х₀ , х) такая, что

Таким образом, если мы используем приближенную формулу f(x) 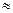T­_n(x), то погрешность определяется остаточным членом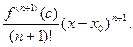

Примеры.

Оценка погрешности линеаризации.

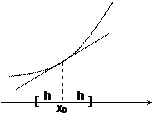Пусть функция f(x) дважды дифференцируема в окрестности точки х₀ . Тогда можно записать .

Пусть х меняется в пределах [x₀–h, x₀+h] и пусть на этом отрезке имеет место оценка |f”(x)| £ M. Тогда ошибка оценивается неравенством

|R(x)| = |0,5f”(c)(x–x₀)²| £ 0,5Mh².

Пример. lnx=x–1 на отрезке [0,9 ; 1,1]. При этом

|R(x)| £ 0,1²/(2×0,9²)=0,0061728.

Ошибка связана с кривизной кривой: чем «кривее» кривая, тем больше ошибка. А кривизна связана со второй производной (см. ниже).

Выпуклость и вогнутость графика функции.

«Крестьянский уровень». Выпуклость – «крышка» , вогнутость – «чашка» .

Возможны варианты названий типа «выпуклость вверх» и «выпуклость вниз».

ТЕОРЕМА. Если кривая выпукла, то она напоминает отрицательную эмоцию L, т.е y”<0, если вогнутость, то J т.е y”>0 .

“Доказательство”: Если «чашка», то a(х) возрастает (см. рис.),

следовательно, tga(х) = y’ возрастает, и поэтому производная

от этой величины положительна, т.е. y”>0;

если «крышка», то a(х) убывает, tga(х) = y’ убывает,

производная от этой величины отрицательна, т.е. y”<0.

ВАРИАНТЫ КРИВЫХ: Возрастающая (убывающая) чашка, y”>0, y’>0, (y’<0);

возрастающая (убывающая) крышка; y”<0, y’>0, (y’<0).

Примеры. .

ТОЧКИ ПЕРЕГИБА. Точка гладкой кривой y=f(x), разделяющая участки выпуклости и вогнутости этой кривой, называется точкой перегиба. При переходе через эту точку разность 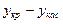меняет знак.

Геометрический смысл: кривая переходит с одной стороны касательной на другую.

Вопрос. Является ли точка М точкой перегиба? Нет. Это точка излома!

ТЕОРЕМА (необходимое условие перегиба). Пусть функция y=f(x) дважды дифференцируема в окрестности точки перегиба х=х₀.и пусть вторая производная непрерывна в некоторой окрестности точки перегиба Тогда f’’(x₀)=0.

Д-во: Если вторая производная не равнялась бы нулю, то по теореме точка х₀ была бы либо точкой выпуклости, либо точкой вогнутости.

Замечание. Обратная теорема «Если f”(x₀)=0, то х₀ – точка перегиба» неверна. Пример .

ДОСТАТОЧНОЕ УСЛОВИЕ ПЕРЕГИБА. Вторая производная обращается в ноль в некоторой точке и меняет знак при переходе через эту точку.

Примеры для полного исследования кривой.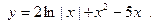

Примечание. Точкой перегиба может также быть точка, в которой f’’(x) не существует. В этой точке должна существовать функция, а f’’(x) должна менять знак при переходе через эту точку.

Примеры.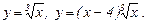

Асимптотика функций в данном процессе.

Определение. Пусть f(x)=g(x)+o(g(x)) , x® x₀ . Тогда функция g(x) называется асимптотикой функции f(x) в процессе x® x₀ .

Другое определение, эквивалентное данному: Функция g(x) называется асимптотикой функции f(x) в процессе x® x₀ , если f(x)~g(x) при x® x₀..

Напомнить теорему о сохранении главного слагаемого и теорему о замене множителя ненулевой константой. Разобрать примеры с построением эскизов графиков:

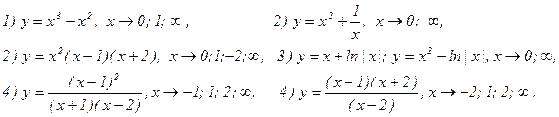
Использование формулы Тейлора для отыскания асимптотики.

Пример. Найти асимптотику функции 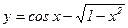при x ® 0 . (y ~ x⁶/6)

Асимптотика на бесконечности для рациональных функций.

Напомнить определение рациональной функции (рациональной дроби).

Правильные и неправильные дроби. Деление «уголком».

Асимптотика на бесконечности. Пример 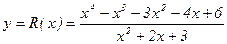. Здесь асимптотика на бесконечности будет у=х². Более точная асимптотика получится при помощи деления «уголком», y=x²–3x.

Если асимптотика на бесконечности линейная (степень числителя на единицу больше степени знаменателя), то она называется АСИМПТОТОЙ.

Пример.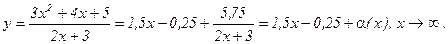

Случаи «степень числителя = степени знаменателя» (горизонтальная асимптота, не совпадающая с осью Х) и «степень числителя < степени знаменателя» (асимптота – ось Х).

Примеры: