Конечные результаты изучения дисциплины математики

Силлабус

дисциплина Математика – Mat 1114

специальность 051102 «Общественное здравоохранение»

Курс	-	первый	Семестр II
Всего	-	2 кредита (90 часов)
Лекции	-	5часов
Практические занятия	-	25 часов
СРСП	-	14 часов
Всего аудиторных	-	44 часов
Самостоятельная работа	-	45 часов
Форма контроля:	-	Экзамен

Алматы, 2013

Силлабус составлен доцентом Аймахановой А.Ш. и старшим преподавателем Раманкуловой А.А. на основе Типовой учебной программы.

Силлабус обсужден на заседании модуля

от «____» _____ 2013 г., протокол №____.

Руководитель модуля, профессорНурмаганбетова М.О.

1. Общие сведения:

Наименование вуза	-	Казахский национальный медицинский университет им. С.Д.Асфендиярова
Модуль	-	Медицинская биофизика и биостатистика
Дисциплина	-	«Математика», код дисциплины Mat1114
Специальность	-	051102 «Общественное здравоохранение»
Объем учебных часов	-	2 кредита (90 ч)
Курс и семестр изучения	-	1 курс, 2 семестр

Сведения о преподавателях модуля:

Аймаханова Айзат Шалхаровна	-	доцент
Раманкулова Алима Абдрамбековна	-	старший преподаватель
Исмаилова Мадина Маликовна	-	старший преподаватель

Контактная информация:

Модуль Медицинская биофизика и биостатистика находится по адресу ул. Богенбай батыра 151, учебный корпус №2, второй этаж (правое крыло), тел. 2926986 внутренние номера 190, 219.

Политика дисциплины.

Студенты обязаны:

- посещать лекции, практические занятия без опозданий, в халатах;

- не пропускать занятия без уважительной причины, в случае отсутствия на занятии по уважительной причине, например, по болезни предоставить разрешение с деканата на отработку пропущенных занятий;

- пропущенные занятия отрабатывать в определенное время, назначенное преподавателем;

- все задания практических занятий должны быть выполнены и оформлены соответственно требованиям;

- все виды работ должны быть сданы в установленные сроки;

- работы, сданные позже установленного срока не расматриваются;

- студенты, не набравшие 30 баллов (50%) за семестр, не сдавшие все контрольные работы и рубежные контроли, к экзамену не допускаются.

2. ПРОГРАММА:

ВВЕДЕНИЕ

Курс математики играет большую роль в формировании активной мировоззренческой позиции студентов. Преподавание физико-математических дисциплин в высших учебных заведениях ставит перед высшей медицинской школой новые задачи, связанные с достижениями современной науки и практики биологии, физики, химии и других естественных наук.

Основной целью курса для студентов является ознакомление студентов с основами современного математического аппарата, как средства решения теоретических и практических задач фармации, физики, биологии, химии и экономики. Математическая подготовка студентов нацелена на развитие и формирование диалектического мышления, выработку умения переводить задачи на математический язык.

Преподавание математики призвано способствовать повышению уровня знаний студентов, формированию у них научно-обоснованного материалистического мировоззрения.

В процессе изучения курса математики студент познакомится с простейшими дифференциальными уравнениями, изучит основные понятия и теоремы теории вероятностей и научится применять их в теории математической статистики, особенно с целью планирования эксперимента и математической обработки полученных результатов.

ЦЕЛЬ ДИСЦИПЛИНЫ

Ø Обучениестудентов специальности общественного здравоохранения основным понятиям математического анализа, теории вероятности и математической статистики.

Ø Обучить методам решения теоретических и практических задач физики, химии.

Ø Формировать и развивать аналитические способности при работе с профессиональной литературой.

Ø Совершенствовать навыки межличностного общения, умение работать в команде.

ЗАДАЧИ ОБУЧЕНИЯ

Ø обучение основным математическим методам, необходимым для анализа и моделирования процессов и явлений, при поиске оптимальных решений и выборе наилучших способов реализации этих решений;

Ø обучение методам обработки и анализа результатов экспериментов;

Ø ознакомление с математическим моделированием медико-биологических процессов;

Ø применение полученных математических знаний при решении конкретных задач, связанных с профессиональной деятельностью, а также задач, возникающих в смежных дисциплинах.

КОНЕЧНЫЕ РЕЗУЛЬТАТЫ ИЗУЧЕНИЯ ДИСЦИПЛИНЫ МАТЕМАТИКИ

В результате усвоения курса “Математики”

студент должен знать:

Ø методы решения простейших дифференциальных уравнений;

Ø способы составления дифференциальных уравнений при решении типовых задач медико-биологического, физико-химического содержаний;

Ø методы вычисления вероятностей случайных событий;

Ø вычисление вероятностей в повторных независимых испытаниях;

Ø определение параметров линейной регрессии методом наименьших квадратов;

Ø определение параметров линейной регрессии методом наименьших квадратов по сгруппированным данным.

уметь:

Ø решать простейшие дифференциальные уравнения;

Ø применять теорию дифференциальных уравнений при решении типовых задач медико-биологического содержания;

Ø вычислять вероятности случайных событий;

Ø оценивать основные характеристики распределений случайных величин;

Ø описывать корреляционную зависимость уравнением линейной регрессии и строить линию регрессии;

Ø обрабатывать и анализировать результаты измерений.

ВЗАИМОСВЯЗЬ С ДРУГИМИ ДИСЦИПЛИНАМИ:

2.5. Пререквизиты: базовый курс математики.

2.6. Постреквизиты:

1. Физиология

2. Фармакология

3. Микробиология

4. Биостатистика

5. Общественное здравоохранение

Краткое содержание дисциплины

Основы математического анализа. Применение математического анализа для моделирования медико-биологических процессов. Элементы теории вероятностей и математической статистики. Обработка и анализ результатов измерений. Математические методы решения интеллектуальных задач и их применение в общественном здравоохранении.

2.8. ТЕМАТИЧЕСКИЙ ПЛАН ЛЕКЦИЙ, ПРАКТИЧЕСКИХ ЗАНЯТИЙ, СРСП, СРС:

ТЕМАТИЧЕСКИЙ ПЛАН ЛЕКЦИЙ:

№ недели	№ п/п	Тема и содержание лекции	Форма проведения	Продолжи-тельность в часах
		Дифференциальное и интегральное исчисление функции одной переменной. Функции нескольких переменных. Предел функции. Понятия производной и дифференциала функции одной переменной. Первообразная функция и неопределенный интеграл. Определенный интеграл. Формула Ньютона – Лейбница. Понятие функции нескольких переменных. Экстремум функции нескольких переменных. Условный экстремум.	Информа-ционное сообщение в форме презентации
		Дифференциальные уравнения. Дифференциальные уравнения с разделяющимися переменными. Линейные дифференциальные уравнения первого порядка. Применение линейных уравнений для решения задач естествознания, фармации и медицины. Уравнения второго порядка, допускающие понижение порядка. Решение дифференциального уравнения . Линейные уравнения второго порядка с постоянными коэффициентами.	Информа-ционное сообщение в форме презентации
		События и вероятность. События. Виды событий. Классическое определение вероятности. Статистическая вероятность. Теоремы сложения и умножения вероятностей. Формула полной вероятности. Формулы Бейеса. Повторение испытаний.	Информа-ционное сообщение в форме презентации
		Случайные величины и их законы распределения. Дискретная и непрерывная случайные величины. Закон распределения. Функция распределения и плотность вероятности. Числовые характеристики случайных величин. Основные законы распределения случайных величин.	Информа-ционное сообщение в форме презентации
		Корреляционно-регрессионный анализ. Статистическая зависимость. Уравнение линейной регрессии. Параметры линейной регрессии. Корреляционная зависимость. Коэффициент корреляции, его смысл и свойства. Проверка значимости коэффициента корреляции.	Информа-ционное сообщение в форме презентации
Итого		5 часов

ТЕМАТИЧЕСКИЙ ПЛАН ПРАКТИЧЕСКИХ ЗАНЯТИЙ:

№ недели	№ п/п	Тема и содержание практического занятия	Форма проведения	Продолжи-тельность в часах
		Непрерывность функции. Предел функции, односторонние пределы. Бесконечно малые и теоремы о бесконечно малых. Свойства непрерывных функций. Точки разрыва функции и их классификация. Решение ситуационной задачи.	Практические навыки, активные методы обучения
		Производная и дифференциал функции одной переменной. Понятие производной функции одной переменной. Правила дифференцирования функций. Понятие дифференциала функции одной переменной. Производные и дифференциалы высших порядков. Тестовый контроль.	Практические навыки, активные методы обучения
		Функции нескольких переменных. Экстремум функции двух переменных. Область определения. Линия уровня. Полный дифференциал. Производная по направлению и градиент функции.Необходимое и достаточное условия экстремума. Наибольшее и наименьшее значения функции. Условный экстремум. Решение ситуационной задачи.	Практические навыки, активные методы обучения
		Интегральное исчисление функции одной переменной. Свойства неопределенного интеграла. Таблица интегралов. Основные методы интегрирования: метод подстановки и интегрирования по частям. Определенный интеграл. Формула Ньютона – Лейбница. Тестовый контроль.	Практические навыки, активные методы обучения
		Дифференциальные уравнения первого порядка. Основные понятия и определения. Уравнения с разделяющимися переменными. Однородное уравнение. Решение ситуационной задачи.	Практические навыки, активные методы обучения
		Линейные дифференциальные уравнения первого порядка. Методы Бернулли и Лагранжа (метод вариации постоянной) для решения линейных дифференциальных уравнений. Решение ситуационной задачи	Практические навыки, активные методы обучения
		Дифференциальные уравнения второго порядка. Уравнения второго порядка, допускающие понижение порядка. Решение дифференциального уравнения 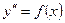. Минивикторина.	Практические навыки, активные методы обучения
		Рубежный контроль №1.	Практические навыки
		События и вероятность. События. Виды событий. Классическое определение вероятности. Статистическая вероятность. Теоремы сложения и умножения вероятностей. Формула полной вероятности. Формулы Бейеса. Повторение испытаний. Тестовый контроль.	Практические навыки, активные методы обучения
		Случайные величины. Дискретная и непрерывная случайные величины. Закон распределения. Функция распределения и плотность вероятности. Числовые характеристики случайных величин. Тестовый контроль.	Практические навыки, активные методы обучения
		Статистическое распределение выборки. Генеральная и выборочная совокупности. Методика обработки статистических данных. Решение ситуационной задачи.	Практические навыки, активные методы обучения
		Линейная регрессия. Виды зависимостей между случайными величинами. Оценка коэффициента регрессии методом наименьших квадратов. Проверка гипотезы о значимости коэффициента регрессии. Тестовый контроль	Практические навыки, активные методы обучения
		Корреляционный анализ. Коэффициент корреляции и его свойства. Проверка значимости коэффициента корреляции. Минивикторина.	Практические навыки, активные методы обучения
		Рубежный контроль №2	Практические навыки
Итого		25 часов

ТЕМАТИЧЕСКИЙ ПЛАН СРСП:

№ недели	№ п/п	Тема и содержание СРСП	Форма проведения	Продолжи-тельность в часах
		Дифференциал функции. Правила нахождения производных и дифференциалов высших порядков.	Коллективное обсуждение
		Функции нескольких переменных. Функции двух и многих переменных. Предел и непрерывность.	Коллективное обсуждение
		Приложения определенного интеграла. Общая схема применения интеграла (схема решения задач, площадь поверхности вращения, давление жидкости на стенку сосуда).	Коллективное обсуждение
		Применение дифференциальных уравнений в задачах естествознания. Составление и решение дифференциальных уравнений на примерах задач физико-химического, медико-биологического содержания.	Коллективное обсуждение
		Неоднородные дифференциальные уравнения с постоянными коэффициентами. Линейные уравнения второго порядка с постоянными коэффициентами. Метод вариации произвольных постоянных.	Коллективное обсуждение
		Повторные независимые испытания. Формулы Бернулли. Локальная и интегральная формулы Муавра-Лапласа.	Коллективное обсуждение
		Основные законы распределения случайных величин. Распределения дискретной случайной величины: Биномиальное и Пуассона. Равномерное и нормальное распределения непрерывной случайной величины. Кривая Гаусса.	Коллективное обсуждение
		Статистические оценки параметров распределения. Оценка генеральной дисперсии по данным выборки.	Коллективное обсуждение
		Построение выборочной линии регрессии. Выборочное уравнение линейной регрессии. Сопоставление наблюдаемых данных с полученной линией регрессии.	Коллективное обсуждение
Итого		14 часов

ТЕМАТИЧЕСКИЙ ПЛАН СРС:

№ недели	№ п/п	Тема	Форма проведения	Продолжи-тельность в часах
		Последовательности и их пределы.	Презентации, реферат, глоссарий, кроссворд, тесты
		Бесконечно малые и бесконечно большие величины.
		Применение дифференциала в приближенных вычислениях.
		Предел и непрерывность функции двух и многих переменных.
		Интегрирование рациональных функций
		Интегрирование иррациональных и тригонометрических функций
		Несобственные интегралы
		Применение линейных дифференциальных уравнений для решения прикладных задач.
		Линейные дифференциальные уравнения второго порядка с правой частью специального вида.
		Закон больших чисел. Неравенство Чебышева и Маркова. Теорема Чебышева.
		Понятие о демографических показателях, расчет общих коэффициентов рождаемости, смертности.
		Применение статистических показателей для оценки деятельности поликлиники и стационара.
		Понятие о множественной корреляции.
Итого		46 часов

2.9. Охват оцениваемых компетенций по курсу «Математика»

	Тема	Вид занятия, количество часов	Охват оцениваемых компетенций
Практические занятия	СРСП	СРС	Знания Max 100%	Практические навыки Max 100%	Коммуникативные навыки Max 100%	Правовая компетенция Max 100%	Самообразование Max 100%
	Последова-тельности и их пределы								Работа с профессиональ-ной литературой
	Непрерыв-ность функции					Решение ситуацион-ной задачи
	Бесконечно малые и бесконечно большие величины								Работа с профессиональ-ной литературой
	Производная и дифференциал функции одной переменной				Тес-тиро-вание
	Применение дифференциа-ла в прибли-женных вычислениях								Работа с профессиональ-ной литературой
	Функции нескольких переменных. Экстремум функции двух переменных					Решение ситуацион-ной задачи
	Предел и непрерывность функции двух и многих переменных								Работа с профессиональ-ной литературой
	Интегральное исчисление функции одной переменной				Тес-тиро-вание
	Интегриро-вание рациональных функций								Работа с профессиональ-ной литературой
	Интегриро-вание ирра-циональных и тригономет-рических функций								Работа с профессиональ-ной литературой
	Несобствен-ные интегралы								Работа с профессиональ-ной литературой
	Дифферен-циальные уравнения первого порядка					Решение ситуацион-ной задачи
	Линейные дифферен-циальные уравнения первого порядка					Решение ситуацион-ной задачи
	Применение линейных дифферен-циальных уравнений для решения прикладных задач								Работа с профессиональ-ной литературой
	Дифферен-циальные уравнения второго порядка						Минивикто-рина
	Линейные дифферен-циальные уравнения второго порядка с правой частью специального вида								Работа с профессиональ-ной литературой
	Рубежный контроль №1					Решение задач
	События и вероятность				Тес-тиро-вание
	Закон больших чисел. Неравенство Чебышева и Маркова. Теорема Чебышева								Работа с профессиональ-ной литературой
	Случайные величины				Тес-тиро-вание
	Статистичес-кое распределение выборки					Решение ситуацион-ной задачи
	Понятие о демографии-ческих показателях, расчет общих коэффициен-тов рождаемости, смертности								Работа с профессиональ-ной литературой
	Применение статистичес-ких показателей для оценки деятельности поликлиники и стационара								Работа с профессиональ-ной литературой
	Линейная регрессия				Тес-тиро-вание
	Корреляцион-ный анализ						Минивикто-рина
	Понятие о множествен-ной корреляции								Работа с профессиональ-ной литературой
	Рубежный контроль №2					Решение задач
	Итого					5+2 р/к		-

Рекомендуемая литература.

на русском языке

Основная:

1. Шипачев В.С. Курс высшей математики. М., «Проспект», 2004г.

2. И.В. Павлушков и др. Основы высшей математики и математической статистики. (учебник для медицинских и фармацевтических вузов) М., «ГЭОТАР - МЕД»; 2003

3. Баврин И.И. Краткий курс высшей математики для химико-биологических и медицинских специальностей.- М.: Физматлит, 2003.

4. В.Е. Гмурман. Теория вероятностей и математическая статистика. М., «Высшая школа», 2001г.

5. В.Е. Гмурман. Руководство к решению задач по теории вероятностей и математической статистики. М., «Высшая школа», 2001 г.

Дополнительная:

1. А. Петри, К. Сэбин Наглядная статистика в медицине. М. ГЭОТАР-МЕД; 2003

2. Е.А. Лукьянова Медицинская статистика. М., РУДН; 2002

3. В.И. Юнкеров, С.Г.Григорьев Математико-статистическая обработка данных медицинских исследований. С.-П., ВМА, 2002

4. А.Н.Ремизов, А.Г.Максина. Сборник задач по медицинской и биологической физике. Москва. 2001г.

на казахском языке

1. Изтлеуов М.К., Беккужина А.И., Жалимбетова Н.К., Ахметова А.Б. Математика: Жоғары медицина оқу орындарына арналған оқулық. Полиграфия, 2005г.

2. Қасымов К., Қасымов Е. Жоғары математика курсы. Оқу қуралы.-Алматы: Санат, 1997.

на английском языке

1. Thomas’ Calculus Georgeb. Thomas, Grasrevised bay Ross L. Finney, Maurise D. Weir, 1989.

2.11. Методы обучения И ПРЕПОДАВАНИЯ:

· Лекции: обзорные и проблемные.

· Практические занятия: семинары, решение ситуационных задач, работа в малых группах; деловые игры, разбор и обсуждение случаев, моделирование ситуаций.

· Самостоятельная работа студентов под руководством преподавателя: работа в парах, решение ситуационных задач, консультации, дискуссии, презентации рефератов, обсуждение результатов выполнения индивидуальных и групповых заданий, математические диктанты.

· Самостоятельная работа студентов: работа с литературой, электронными базами данных и компьютерными обучающими программами, решение ситуационных задач; составление глоссария, планов приготовления раствора, решение тестовых заданий, подготовка и защита научных рефератов

2.12. кРИТЕРИИ И ПРАВИЛА оценки знаний:

Итоговая оценка складывается из рейтинга допуска и оценки итогового контроля:

гдеI – итоговая оценка, R– оценка рейтинга допуска, E – оценка итогового контроля (экзамен по дисциплине).

Итоговый рейтинг состоит из 60% рейтинга допуска и 40% оценки итогового контроля.

Итоговый контроль: интегрированный экзамен, состоит их двух этапов: 1) тестирование, 2) устный (по билетам)

где 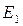_- баллы за I этап экзамена, _– баллы за II этап экзамена.

Рейтинг допуска в итоговой оценке студента составляет не менее 60 %, определяется по формуле

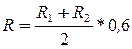
где - первый рейтинг контроль, – второй рейтинг контроль

Рейтинг контроль определяется по формуле , где – текущий контроль, - первый рубежный контроль, – второй рубежный контроль

Текущий контроль –оценка уровня сформированности компетенций

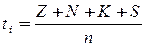
где	n:	-	количество заданий по всем компетенциям
	Z:	z1+z2+…+z5	-	Оценки за знания
	N:	n1+n2+n3	-	Оценки за навыки
	K:	k1+k2	-	Оценки за коммуникативные компетенции
	P:		-	Оценки за правовые компетенции
	S:	s1+ s2	-	Оценки за СРС

Критерии оценки знаний студентов:

Тестирование – максимально 100%.

Ситуационная задача – максимально 100 %:

Критерий	Процентное содержание
Выполнение всего задания, без ошибок, с правильным оформлением
Выполнение всего задания, с правильным оформлением, с небольшими ошибками в вычислениях	90-99
Выполнение 75% задания, с небольшими ошибками в расчетах и оформлении	75-89
Выполнение 50% задания, без ошибок	50-74
Выполнение менее 50% заданий, или решение с грубыми ошибками в применении формул	0-49

Устный опрос:

Критерий	Процентное содержание
полный ответ	90-100
допущены незначительные ошибки	75-89
допущены принципиальные ошибки или неполный ответ	50-74
незнание материала

Минивикторина:

Коммуникативный навык	Алгоритм	Процентное содержание
Активное слушание	Подавать сигналы внимательного слушания. Задавать конкретизирующие вопросы. Проверить свое понимание. Интерпретация.
Привлечение внимания слушателя	Открытая поза, демонстрация на невербальном уровне дружеского настроя. Умение задавать вопросы и контролировать беседу. Умение подводить и понятно аргументировать свою позицию.
Высказывание конструктивной критики	Наблюдательность. Без эмоциональное высказывание. Умение выделить положительные и отрицательные стороны к конкретной ситуации. Соответствие вербальной и невербальной информации.
Выдерживание конструктивной критики	Умение слышать и слушать. Дать возможность высказаться собеседнику. Применение соответствующих выразительных и ободряющих замечаний.
Эмоциональная поддержка собеседника	Понимание очевидной эмоциональной и физической слабости человека
Разрешение конфликтной ситуации	Умение видеть проблему с точки зрения собеседника. Умение находить компромисс. Умение интерпретировать.

Общая оценка по коммуникативной компетенции равна среднеарифметическому значению всех коммуникативных навыков.

СРС (максимально 100 %)

Критерий	Процентное содержание
Полное выполнение всех требований соответствующей формы СРС	90-100
Допущены незначительные ошибки, неточное выполнение задания	75-89
Допущены значительные ошибки, неполное выполнение заданий	50-74
Допущены принципиальные ошибки, невыполнение заданий, несоответствие критериям СРС	10-49
Отсутствие СРС

Рубежный контроль:

Тестирование – максимально 100%.

Решение контрольных заданий – максимально 100%.

Критерий	Процентное содержание
Выполнение всего задания, без ошибок, с правильным оформлением
Выполнение всего задания, с правильным оформлением, с небольшими ошибками в вычислениях	90-99
Выполнение 75% задания, без ошибок, с правильным оформлением	80-89
Выполнение 75% задания, с небольшими ошибками	75-79
Выполнение 50% задания, без ошибок	50-74
Выполнение менее 50% заданий, или решение с грубыми ошибками в применении формул	0-49

В случае получения на экзамене 0 баллов, студент остается на повторное изучение дисциплины (т.е. летний семестр).

Время консультаций и экзаменов:

Консультации и экзамены проводятся во время сессии по расписанию ОП и КУП