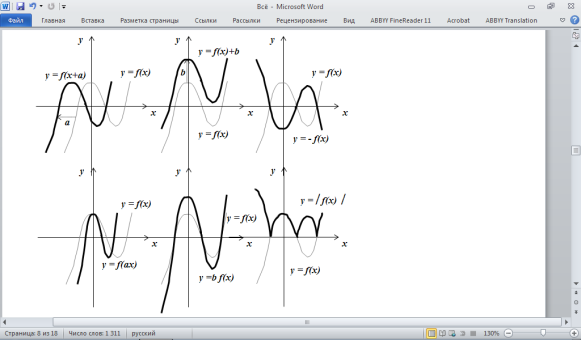
Преобразование графика функции

Арифметическая прогрессия

Определение: Последовательность, у которой задан первый член a₁, а каждый следующий равен предыдущему, сложенному с одним и тем же числом d, называется арифметической прогрессией:

a_n+1 = a_n + d, где d – разность прогрессии.

Арифметический квадратный корень

Биссектриса

Биссектриса – отрезок, выходящий из вершины треугольника и делящий угол пополам.

· Биссектриса делит противолежащую сторону на части , пропорциональные прилежащим сторонам: a_b : a_c = b : c

· Биссектриса делит площадь треугольника, пропорционально прилежащим сторонам.

Вписанная окружность

Центр окружности, вписанной в треугольник, лежит на пересечении биссектрис треугольника.

Если окружность вписана в произвольный четырехугольник, тогда попарные суммы противолежащих сторон равны между собой: a + b = c + d

5. Выпуклый четырёхугольник

Геометрическая прогрессия

Определение: Последовательность, у которой задан первый член b₁ ¹ 0, а каждый следующий равен предыдущему, умноженному на одно и то же число q ¹ 0, называется геометрической прогрессией:

b_n+1 = b_n q, где q – знаменатель прогрессии.

Деление с остатком

Формула деления с остатком: n = m×k + r,

где n – делимое, m - делитель, k - частное, r – остаток: 0 £ r < m

Любое число можно представить в виде:

n = 2k + r, где r = {0; 1}

или n = 4k + r, где r = {0; 1; 2; 3}

Делимость натуральных чисел

Пусть n : m = k, где n, m, k – натуральные числа.

Тогда m – делитель числа n, а n – кратно числу m.

Число n называется простым, если его делителями являются

только единица и само число n.

Множество простых чисел: {2; 3; 5; 7; 11; 13; . . .; 41; 43; 47 и т.д.}

Числа n и m называются взаимно простыми, если у них нет общих делителей, кроме единицы.

Десятичные числа

Стандартный вид: 317,3 = 3,173× 10² ; 0,00003173 = 3,173× 10^-5

Форма записи: 3173 = 3× 1000 + 1× 100 + 7× 10 + 3

Длина окружности, площадь

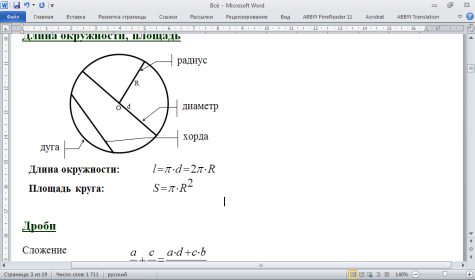
Дроби

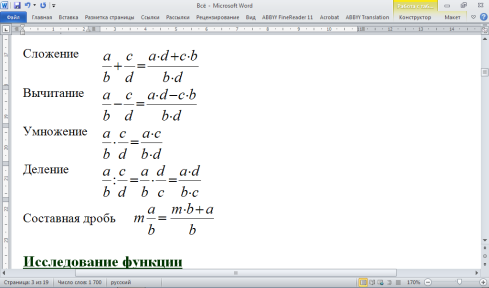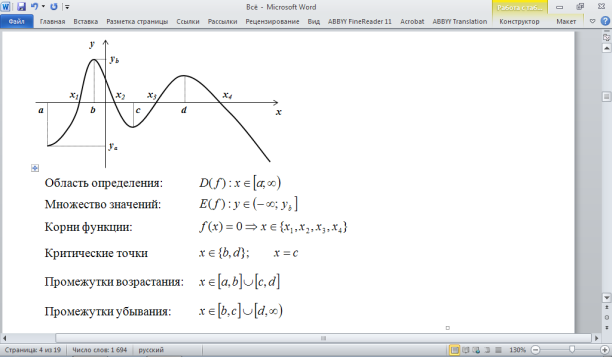
Исследование функции

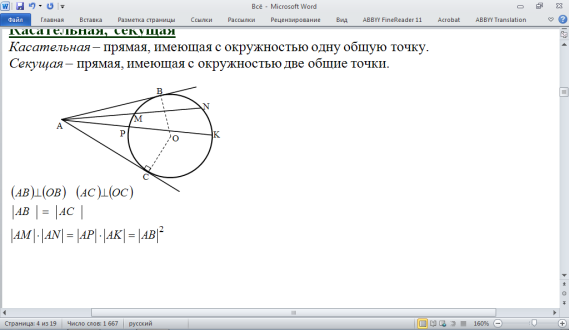
Касательная, секущая

Касательная – прямая, имеющая с окружностью одну общую точку.

Секущая – прямая, имеющая с окружностью две общие точки.

Квадрат

Прямоугольник, у которого все стороны равны, называется квадратом.

Квадратная функция

Квадратное уравнение

Линейная функция

y = kx + b, k – угловой коэффициент, b – свободный член

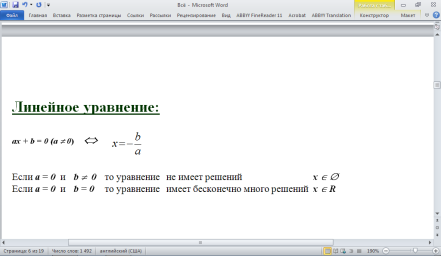
18. Линейное уравнение:

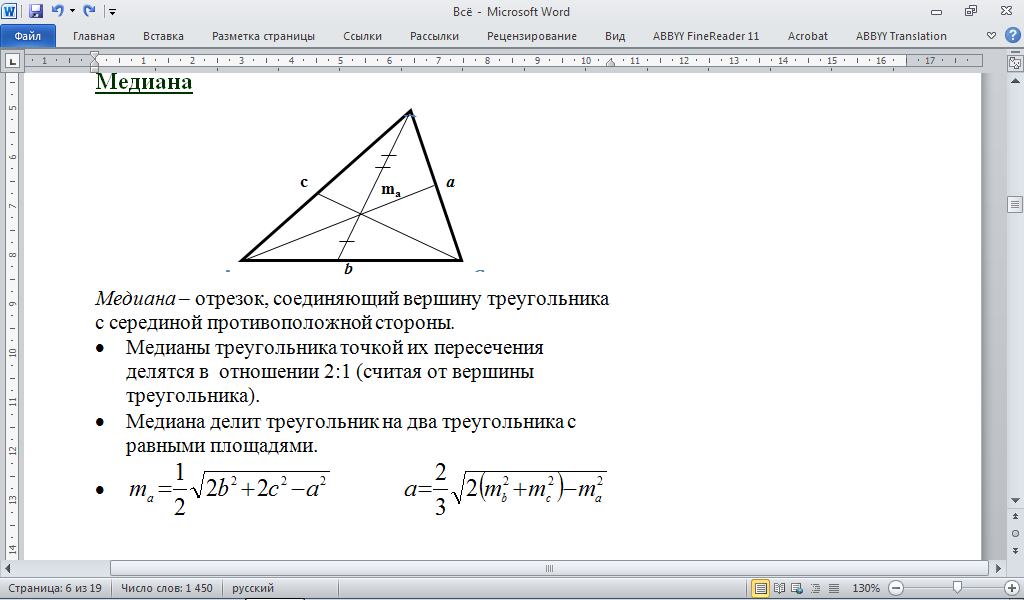
Медиана

Метод интервалов

21. Модуль: уравнения и неравенства

Модуль

Неравенства

Определения:

Неравенством называется выражение вида:

a < b (a £ b), a > b (a ³ b)

Описанная окружность

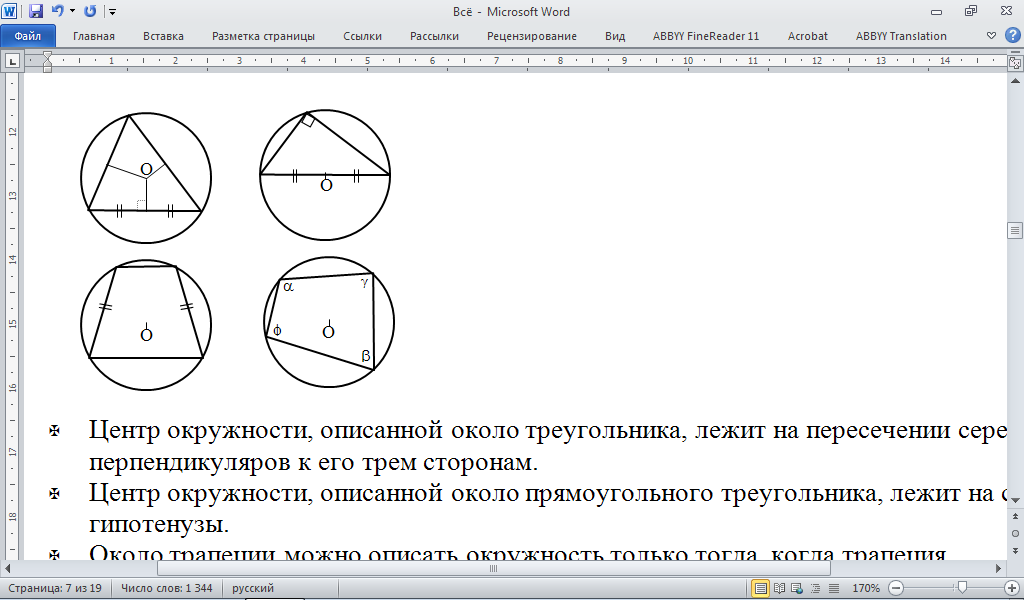
-Центр окружности, описанной около треугольника, лежит на пересечении серединных перпендикуляров к его трем сторонам.

-Центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы.

-Около трапеции можно описать окружность только тогда, когда трапеция равнобочная.

-Если окружность описана около произвольного четырехугольника, тогда попарные суммы противолежащих углов равны между собой:

Периодическая дробь

Площадь треугольника

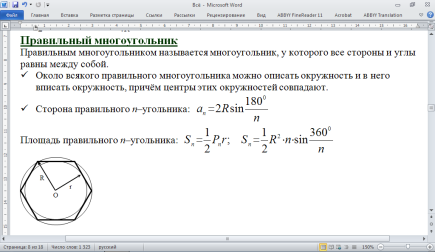
Правильный многоугольник

Правильным многоугольником называется многоугольник, у которого все стороны и углы равны между собой.

ü Около всякого правильного многоугольника можно описать окружность и в него вписать окружность, причём центры этих окружностей совпадают.

Преобразование графика функции