Операции, определяющие формирование множества рациональных чисел

Практическая необходимость перечислять предметы привела к формированию понятия натурального ряда. Практическая же необходимость арифметических операций над натуральными числами приводит к формированию более широкого класса величин - рациональным числам. Схематично это выглядит так:

Натуральный ряд N	L	Операция сложения “+”; операция вычитания " - " обратная к сложению		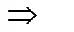Множество Z целых чисел (положительные, отрицательные и ноль)
Множество Z	L	Операция умножения “х”; обратная операция “:” деление.		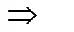Множество Q рациональных чисел вида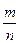

Схема 2

Вывод 1.

Множество чисел представимых в виде несократимых дробей m/n, где: m, n, N, n 0 называется множеством рациональных чисел и обозначается Q. На этом множестве определим операции ±, ´, :, и результат действия этих операций над рациональными числами есть снова рациональное число.

Мы не будем обсуждать все свойства рациональных чисел, а ограничимся напоминанием свойств систематического представления рациональных чисел, известных из элементарного курса математики.

Наличие операций сложения и умножения позволяет построить представление целых чисел при помощи алфавита, содержащего К знаков, называемых цифрами.

Такое представление дается записью вида: 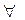aN

a = a_nKⁿ+... + a₁K+a_o (5)

и называется систематической К-ичной записью по основанию К. Символы a_o, a₁, ... , a_n принимают одно из К значений 0,1,2, ... , K-1. Если K 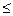10, то для обозначения K цифр используют первые К цифр десятичной системы 0,1,2, ... , К-1. Для обозначения степеней оснований (классов) К¹, К², ..., Кⁿ используются уже введенные числовые обозначения (классы “тиражируются медленнее”, чем числа, входящие в эти классы).

Запись целых чисел в K-ичной системе позволяет реализовать арифметические операции над рациональными числами в виде некоторых алгоритмов, то есть правил выполнения последовательности простых операций над цифрами, представляющими рациональные числа.

В школьном курсе изучаются алгоритмы арифметических операций в десятичной системе.

Напомним для примера алгоритм сложения целых чисел.

Пусть а = 247 = 2 ^. 10² +4 ^. 10+7, в = 378 = 3 ^. 10² + 7 ^. 10 + 8

Найти С = а+в.

Складывая цифры, нумерующие разряды единиц, десятков и сотен, получаем:

7+8 = 10+5 (единицы)

4 ^.10 + 7 ^. 10 = 10²+10 (десятки)

2 ^. 10² + 3 ^. 10² = 5 ^. 10² (сотни)

Учитывая правила формирования разрядов, составляем десятичную запись числа С= а+в:

С = (10² +5 ^. 10²) + (10+10)+5 = 6 ^. 10² +2 ^. 10+5 = 625

Кроме реализации арифметических операций, систематическое представление чисел дает алгоритм сравнения чисел по величине.

Для сравнения целых положительных чисел достаточно сравнить цифры разрядов по старшинству, например: 197<211, так как 197<2^.10², а 211 > 2^.10².

Алгоритм представления рационального числа 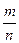в десятичной записи приводит к двум типам записи, известным из школьного курса.

Всякое рациональное число может быть представлено конечной десятичной дробью вида:

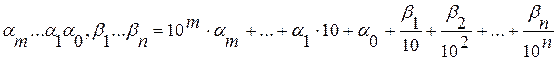, (6)

либо бесконечной периодической дробью вида:

(7)

Напомним так же, что алгоритм представления рационального числа в виде (6) или (7) основан на следующем свойстве целых чисел.

Для любых a, b N , (a > b) существуют m, n N,(m<a, n<b) такие, что

а = bm+n (8)

Вывод 2.