Показательное распределение непрерывной случайной величины
Определение.Показательным (экспоненциальным)называется распределение вероятностей непрерывной случайной величины Х, плотность вероятности которой определяется формулой
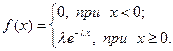
где l - положительное число. Найдем закон распределения.
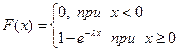
Графики функции распределения и плотности распределения:
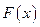
l 1
0 x 0 x
Найдем математическое ожидание случайной величины, подчиненной показательному распределению:
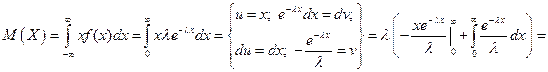
Результат получен с использованием того факта, что
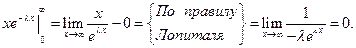
Для нахождения дисперсии найдем величину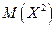 
:
.
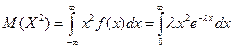Дважды интегрируя по частям, аналогично рассмотренному случаю, получим:
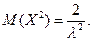
Тогда 
Таким образом: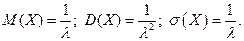 
Очевидно, что в случае показательного распределения математическое ожидание и среднее квадратическое отклонение равны.
Также легко определить и вероятность попадания случайной величины, подчиненной показательному закону распределения, в заданный интервал:
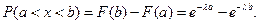
Показательное распределение широко используется в теории надежности.
Допустим, некоторое устройство начинает работать в момент времени 
, а через какое– то время t происходит отказ устройства.
Обозначим Т непрерывную случайную величину – длительность безотказной работы устройства.
Таким образом, функция распределения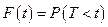 
определяет вероятность отказа за время длительностью t.
Вероятность противоположного события (безотказная работа в течение времени t) равна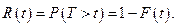 
Определение.Функцией надежности
называют функцию, определяющую вероятность безотказной работы устройства в течение времени t.
Часто на практике длительность безотказной работы подчиняется показательному закону распределению.
Вообще говоря, если рассматривать новое устройство, то вероятность отказа в начале его функционирования будет больше, затем количество отказов снизится и будет некоторое время иметь практически одно и то же значение. Затем (когда устройство выработает свой ресурс) количество отказов будет возрастать.
Другими словами, можно сказать, что функционирование устройства на протяжении всего существования (в смысле количества отказов) можно описать комбинацией двух показательных законов (в начале и конце функционирования) и равномерного закона распределения.
Функция надежности для какого- либо устройства при показательном законе распределения равна:
Данное соотношение называют показательным законом надежности.
Важным свойством, позволяющим значительно упростить решение задач теории надежности, является то, что вероятность безотказной работы устройства на интервале времени t не зависит от времени предшествующей работы до начала рассматриваемого интервала, а зависит только от длительности времени t.
Таким образом, безотказная работа устройства зависит только от интенсивности отказов l и не зависит от безотказной работы устройства в прошлом.
Так как подобным свойством обладает только показательный закон распределения, то этот факт позволяет определить, является ли закон распределения случайной величины показательным или нет.