Общая система уравнений подземной гидромеханики

Для нестационарного процесса при отсутствии источников и стоков имеем:

· уравнение неразрывности

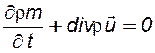; (2.4)

· уравнение сохранения количества движения

. (2.5)

В уравнении (2.5):

· в виду незначительности изменения количества движения во времени первым членом можно пренебречь;

· разница в перетоках количества движения через границы контрольных объёмов также составляют величины второй малости по сравнению со скоростями и, следовательно, вторым членом тоже можно пренебречь;

· силу сопротивления F_cпо аналогии с трубной гидравликой или задачами обтекания можно представить в виде

.

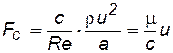Таким образом, уравнение (2.2) вырождается в следующее

,

то есть, получаем уравнение, линейно связывающее скорость фильтрации с градиентом давления.

Уравнение такого вида широко используется в подземной гидродинамике и носит название уравнения фильтрации в форме Дарси:

, (2.6)

где р*=р+zrg, z – вертикальная координата.

Движение жидкости может быть установившимся (стационарным) и неустановившимся (нестационарным). При установившемся движении параметры потока (плотность, скорость фильтрации и так далее) в каждой точке пористой среды постоянны и не зависят от времени. Таким образом, для установившейся фильтрации и уравнение неразрывности принимает вид

. (2.7)

В вышеприведенных уравнениях:

;

;

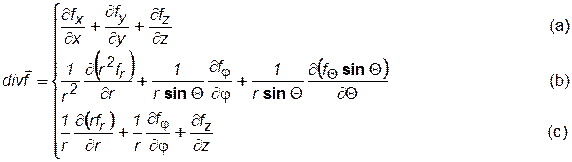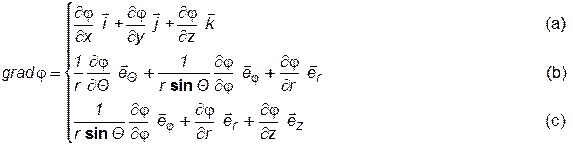(a) – декартовые координаты; (b) – сферические координаты; (c) – цилиндрические координаты; i, j, k– единичные векторы по осям декартовой системы координат;e_Q , e_j , e_r, e_z – по осям сферической системы; Q, j, r и z – по осям цилиндрической системы; в сферических координатах – угол Qопределяет изменение меридианного угла, а угол j– широтного.

Для несжимаемой жидкости (r=сonst) уравнение (2.3) запишется в виде

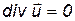. (2.8)

2.3. Закон Дарси (линейный закон фильтрации)

Пористая среда

В 1856г. французским инженером Дарси был установлен основной закон фильтрации – закон Дарси или линейный закон фильтрации, устанавливающий линейную связь между потерей напора Н₁-Н₂ и объёмным расходом жидкости Q, текущей в трубке с площадью поперечного сечения F ,заполненной пористой средой.

Закон Дарси имеет вид

, (2.9)

где с – коэффициент пропорциональности, называемый коэффициентом фильтрации и имеющий размерность скорости; – гидравлический напор при пренебрежении скоростным напором; р/g – пьезометрическая высота.

Запишем закон Дарси в дифференциальной форме, учитывая соотношение u=Q/F,

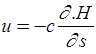(2.10)

или в векторной форме

, (2.11)

где s – расстояние вдоль оси криволинейной трубки тока.

Коэффициент фильтрации «с» характеризует среду и жидкость одновременно. Этот коэффициент обычно используется в гидротехнических расчетах, где приходится иметь дело с одной жидкостью – водой. При наличии различных жидкостей, что чаще бывает в подземной гидромеханике, использовать его неудобно. Поэтому закон Дарси записывается обычно в несколько ином виде

(2.12)

или

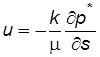. (2.13)

Из сравнения (2.10) и (2.12) имеем

. (2.14)

Границы применимости закона Дарси.Закон Дарси справедлив при соблюдении следующих условий:

a) скорость фильтрации и градиент давления малы;

b) изменение скорости фильтрации и градиента давления малы.

При повышении скорости движения жидкости закон Дарси нарушается из-за увеличения потерь давления на эффекты, связанные с инерционными силами: образование вихрей, зон срыва потока с поверхности частиц, гидравлический удар о частицы и т.д. Это так называемая верхняя граница. Закон Дарси может нарушаться и при очень малых скоростях фильтрации в процессе начала движения жидкости из-за проявления неньютоновских реологических свойств жидкости и её взаимодействия с твёрдым скелетом пористой среды. Это нижняя граница.

Верхняя граница. Критерием верхней границы справедливости закона Дарси обычно служит сопоставление числа Рейнольдса Re=war/μ с его критическим значением Re_кр, после которого линейная связь между потерей напора и расходом нарушается. В выражении для числа Re:w –характерная скорость течения: а – характерный геометрический размер пористой среды; r – плотность жидкости. Имеется ряд представлений чисел Рейнольдса, полученных различными авторами при том или ином обосновании характерных параметров. Наиболее часто в нефтегазопромысловой практике применяется зависимость Щелкачёва:

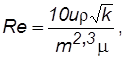(2.15)

где

Критическое число Рейнольдса Re_кр=1–12.

Скорость фильтрации u_кр, при которой нарушается закон Дарси, называется критической скоростью фильтрации. Нарушение скорости фильтрации не означает перехода от ламинарного движения к турбулентному, а вызвано тем, что силы инерции, возникающие в жидкости за счёт извилистости каналов и изменения площади сечения, становятся при u>u_кр соизмеримы с силами трения.

При обработке экспериментальных данных для определения критической скорости пользуются безразмерным параметром Дарси

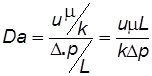, (2.16)

представляющим собой отношение сил вязкого трения к силе давления. В области действия закона Дарси данный параметр равен 1 и уменьшается при превышении числа Re критического значения.

Нижняя граница. При очень малых скоростях с ростом градиента давления изменение скорости фильтрации не подчиняется закону Дарси. Данное явление объясняется тем, что при малых скоростях становится существенным силовое взаимодействие между твердым скелетом и жидкостью за счет образования аномальных, неньютоновских систем, например, устойчивые коллоидные растворы в виде студнеобразных плёнок, перекрывающих поры и разрушающихся при некотором градиенте давленияt_н , называемого начальным и зависящим от доли глинистого материала и величины остаточной водонасыщенности. Имеется много реологических моделей неньютоновских жидкостей, наиболее простой из них является модель с предельным градиентом

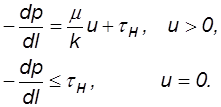. (2.17)

Законы фильтрации при Re > Re_кр. От точности используемого закона фильтрации зависит достоверность данных исследования скважин и определение параметров пласта. В связи с этим, в области нарушения действия закона Дарси необходимо введение нелинейных законов фильтрации. Данные законы могут быть: одночленными и двухчленными.

Одночленные законы описываются степенной зависимостью вида

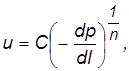(2.18)

где C, n – постоянные, 1£ n £ 2.

Данные зависимости неудобны, так как параметр n в общем случае зависит от скорости фильтрации. В связи с этим, наибольшее употребление нашли двучленные зависимости, дающие плавный переход от закона Дарси к квадратичному закону Краснопольского:

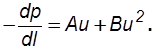(2.19)

Коэффициенты А и В определяются либо экспериментально, либо теоретически. В последнем случае

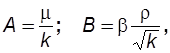(2.20)

где b– структурный коэффициент и по Минскому определяется выражением

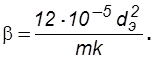(2.21)

Трещинная среда

Линейный закон фильтрации.В трещинных пластах скорость фильтрации связана со средней скоростью через трещиноватость

u=m_тw. (2.22)

Средняя скорость выражается через градиент давления по формуле Буссинеска при представлении течения по трещинам, как течения между двумя плоскими параллельными пластинами

(2.23)

Если использовать зависимости (2.23), (1.12), то получаем линейный закон фильтрации в трещинных средах

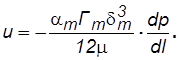(2.24)

Проницаемость трещинных сред равна

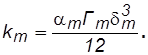(2.25)

Для трещинно-пористой среды общая проницаемость определяется как сумма пористой и трещинной проницаемостей.

Трещинно-пористую среду следует считать деформируемой. При таком подходе проницаемость трещинного пласта будет изменяться с изменением давления, а именно:

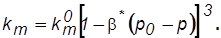(2.26)

Данная зависимость справедлива при небольших изменениях давления. В общем случае необходимо использовать экспоненциальную связь деформации трещин с давлением.

Границы применимости линейного закона фильтрации.Так же, как и в пористых средах, в трещинных породах линейный закон может нарушаться при больших скоростях фильтрации из-за появления значительных по величине сил инерции. При этом значения критических чисел Рейнольдса значительно зависят от шероховатости: для гладких трещин Re_кр=500, а для шероховатых трещин – 0,4. Следует заметить, что если величина относительной шероховатости меньше 0.065, то её ролью в процессе фильтрации можно пренебречь.

Для трещинной среды выражение для числа Рейнольдса получается аналитически и равно

, а Re_кр=0,4. (2.27)