Задачи, приводящие к расширению множества рациональных чисел

Решение задач, имеющих практический интерес, не исчерпывается арифметическими операциями над числами. Рассмотрим следующие две задачи.

Задача 1.

Измерить длину диагонали квадрата, считая, что единица длины есть сторона этого квадрата.

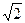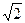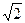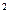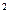Теорема Пифагора дает результат: искомая длина равна . Предположение о том, что = P/q – рациональное число опровергается известным доказательством от противного. Предположим, что = P/q Þ p = 2q Þ p=2k Þ 2q 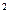= 4k 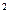Þ q = 2m Þ 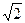= p/q.

Заметим, что величина 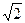является решением уравнения x 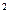-2=0. Действительные рациональные числа, являющиеся решениями алгебраических уравнений

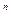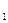x + a x 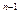+ … +a 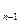x + a = 0 (10)

с целочисленными коэффициентами a 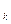Î Z, k=1, …, n, называются алгебраическими числами. Таким образом, число 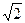является алгебраическим числом и является результатом алгебраической операции – извлечения корня.

Карл Фридрих Гаусс (1777 – 1855) доказал, см., например, [4], стр. 63, что алгебраические числа являются либо целыми числами, либо не представимы в виде p/q ни для каких целых p, q Î Z.

Задача 2.

Измерить длину окружности, считая, что диаметр этой окружности есть единица длины.

Длина окружности L = 2pR, где R – радиус. В нашем случае L=3,1415… . Число p не является ни рациональным, ни алгебраическим, [4]. То, что число p не является рациональным числом, впервые было установлено в 1761 г. французским математиком Иоганном Генрихом Ламбертом (1728 – 1777).

Подчеркнем, что число p не является результатом применения алгебраических операций. Оно может быть выражено согласно алгоритму Ф. Гаусса [5], стр. 41, который представляет последовательность некоторых простых операций, пронумерованных числами натурального ряда.

Вывод 3.

Существуют числа, не являющиеся результатом конечного числа арифметических операций над целыми числами и не представимые в виде p/q ни для каких целых p, q.

Числа, не представимые в виде p/q ни для каких целых p, q, называются иррациональными.

Аксиоматизация множества действительных чисел.

Конструктивное построение множества действительных чисел можно представить в виде схемы.

Непрерывными операциями мы называем вычислительные алгоритмы, состоящие из арифметических и других простых операций, пронумерованных натуральным рядом. Описание непрерывных операций потребует разработки вспомогательных понятий. Избежать такой дополнительной работы можно аксиоматическим заданием множества действительных чисел.

Добавим к аксиомам, определяющим в П. З. множество рациональных чисел Q, еще одну, следующую аксиому.