Моделирование на макроуровне

Модели макроуровня получаются, когда происходит переход от распределенных параметров к сосредоточенным – выделяются крупные элементы объектов и их параметры сосредоточиваются в одной точке: масса балки оказывается сосредоточенной в центре тяжести, поле потенциалов характеризуется величиной одного напряжения, поток электронов моделируется электрическим током и т. п. Происходит дискретизация пространства, однако время – по-прежнему непрерывная величина. Математическими моделями на макроуровне являются обыкновенные дифференциальные или интегро-дифференциальные уравнения.

Поведение (состояние) моделируемых объектов, состоящих из физически однородных элементов, в которых описываются процессы определенной физической природы (механические, электрические, гидравлические, тепловые), можно характеризовать с помощью фазовых переменных двух типов – типа потенциала и типа потока.

В табл. 1.2 приведены типы фазовых переменных для объектов разной физической природы.

Таблица 1.2

Фазовые переменные для различных физических систем

Система	Фазовые переменные
типа потенциала	типа потока
Электрическая	Электрическое напряжение	Электрический ток
Механическая	Скорость	Сила
Механическая вращательная	Угловая скорость	Вращательный момент
Тепловая	Температура	Тепловой поток
Гидравлическая и пневматическая	Давление	Расход

В большинстве технических объектов можно выделить три типа пассивных простейших элементов:

· типа R – элемент рассеивания (диссипации) энергии (как правило, преобразования энергии в тепловую и ее рассеивания);

· типа C и типа L – элементы накопления потенциальной и кинетической энергии.

Кроме пассивных элементов, существуют два активных элемента – источник напряжения и источник тока.

Уравнения, описывающие свойства элементов объекта, называют компонентными. В них входят переменные типа потенциала и типа потока. Способ связи элементов отражается с помощью других уравнений, которые называют топологическими. В них входят переменные одного типа: либо потенциала, либо потока. Топологические уравнения могут выражать законы сохранения, условия непрерывности, равновесия, баланса и т. п.

Математические модели объектов есть совокупность компонентных и топологических уравнений.

Рассмотрим примеры компонентных и топологических уравнений для некоторых разных по своей физической природе объектов.

Электрические системы

Основными фазовыми переменными электрических систем являются напряжения и токи в различных элементах систем. Компонентные уравнения элементов имеют вид

,

где U – напряжение;

I – ток;

R – сопротивление;

C – емкость;

L – индуктивность.

При соединении резисторов, емкостей, индуктивностей между собой образуется схема, соединение элементов в которой отражается топологическими уравнениями. Ими являются законы Кирхгофа:

,

где уравнения токов записываются для узлов, а уравнения напряжений для контуров. В ЭЭС имеются достаточно сложные элементы, и при их моделировании применяют схемы замещения, состоящие из сопротивлений, емкостей и индуктивностей.

Механическая система

Элементами механических поступательных систем являются:

· элементы механического сопротивления, отражающие потери механической энергии на разные виды трения;

· элементы масс, отражающие свойства инерционности;

· элементы гибкости, отражающие свойства упругости.

Роль фазовых переменных в механических системах выполняют либо силы и скорости, либо силы и перемещения.

Компонентные уравнения имеют вид

,

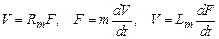где V – скорость;

F – сила;

R – коэффициент, учитывающий зависимость силы трения от скорости;

m – масса-аналог электрической емкости;

L_m – гибкость – параметр, являющийся аналогом электрической индуктивности.

Первое выражение в (1.14) указывает на связь скорости и силы через коэффициент вязкого трения 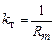. Второе выражение является вторым законом Ньютона. Третье выражение в (1.14) получено из уравнения перемещения пружины x под действием силы F = kx, где k – коэффициент жесткости пружины. После дифференцирования последнего выражения получаем

.

Если обозначить 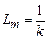(механическая гибкость), то получим третье выражение в (1.14).

Топологические уравнения механической системы выражают уравнение равновесия сил, являющееся аналогом первого закона Кирхгофа, и уравнение сложения скоростей, в соответствии с которым сумма абсолютной, относительной и переносной скоростей равна нулю (аналог второго закона Кирхгофа).

.
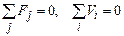